该系列为DR_CAN自动控制原理视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 一个简单的例子
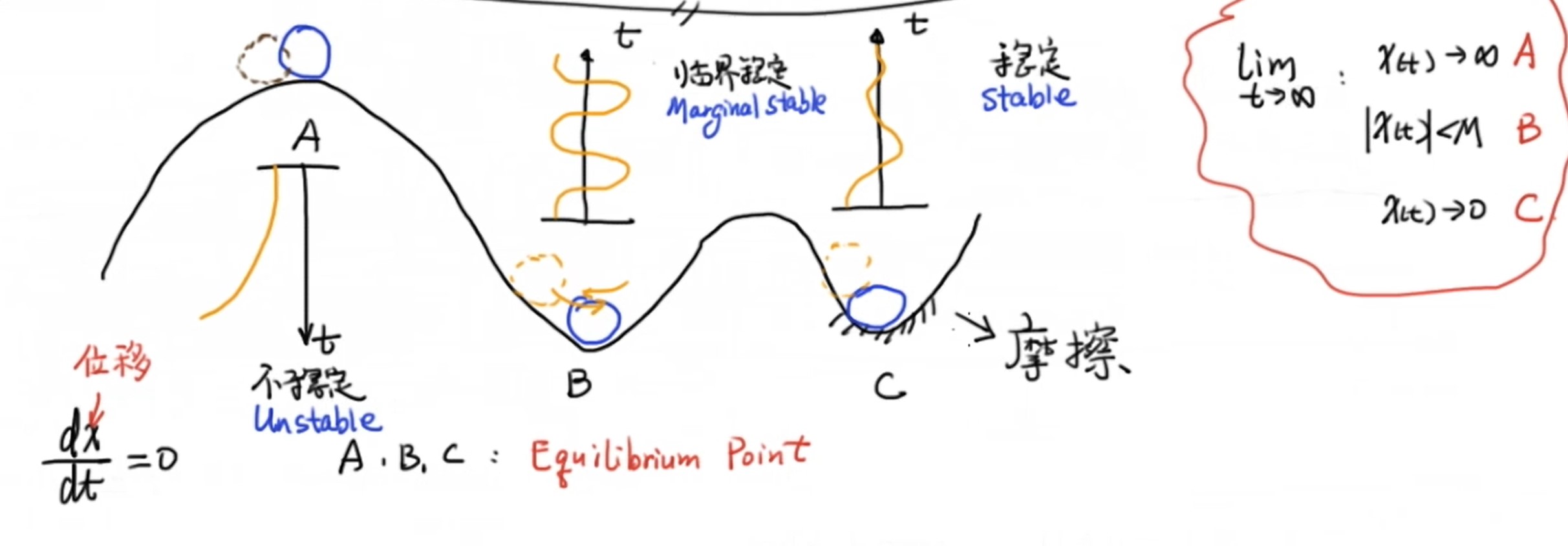
我们假设在一段高低起伏的曲线上的ABC三点分别放一个小球,我们可以发现在没有外界扰动的情况下这三个小球均可以保持静止。但当我们分别给三个小球一个扰动时,A点的小球就会滑落,B点小球则会不断地振荡但始终保持在B点周围,而C点小球由于曲面上的摩擦,最终会重新静止。这种情况用数学语言来描述即图片右侧部分,
其中A点状态称为不稳定(Unstable),B点称为临界稳定(Marginally stable),而C点称为稳定(Stable)。
如果我们对B小球的扰动不大,就可以让它始终保持在B点周围。即系统的输入有界,进而系统的输出也有界,这就是BIBO(Bounded-Input Bounded-Output)稳定。
2 分析传递函数
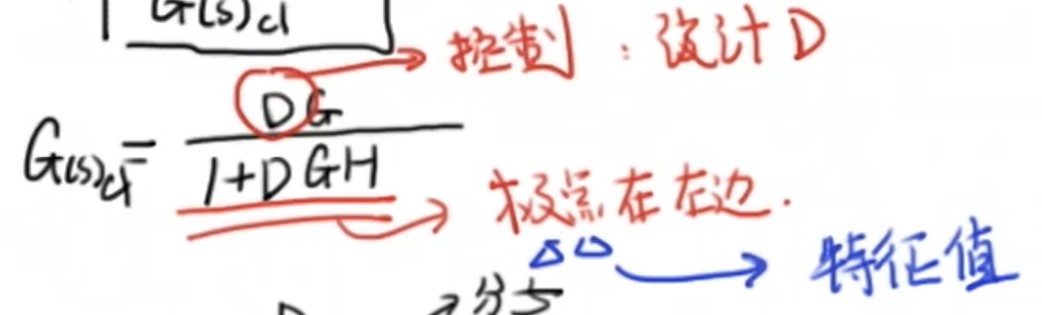
在研究系统稳定性时,一般以单位冲激函数 (delta(t)) 作为输入,就相当于刚才例子中的扰动,而单位冲激函数经过拉普拉斯变换后的值为1,这时系统的输出就等于传递函数本身,这就是为什么常用传递函数本身来分析稳定性。其中 (G(s)) 为系统开环传递函数,(G(s)_{cl}) 为系统闭环传递函数,cl即close loop。
对于单位冲激函数 (delta(t)) 可参考DR_CAN的一期视频:https://www.bilibili.com/video/av26448770

一个传递函数可以抽象成以下形式,令分子等于0的点为系统的零点,而令分母等于0的点是系统的极点,通过分析系统极点的位置,我们就可以了解系统的稳定性。
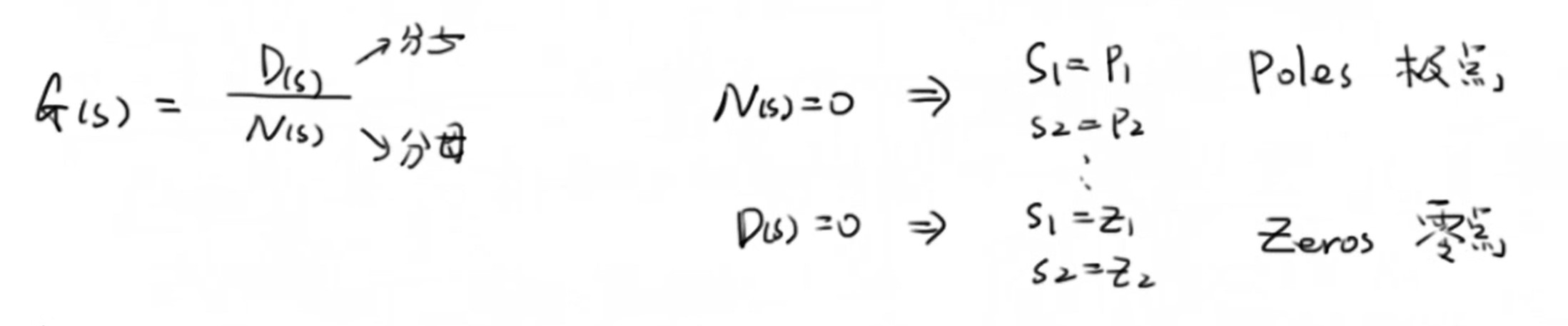
3 另两个简单的例子
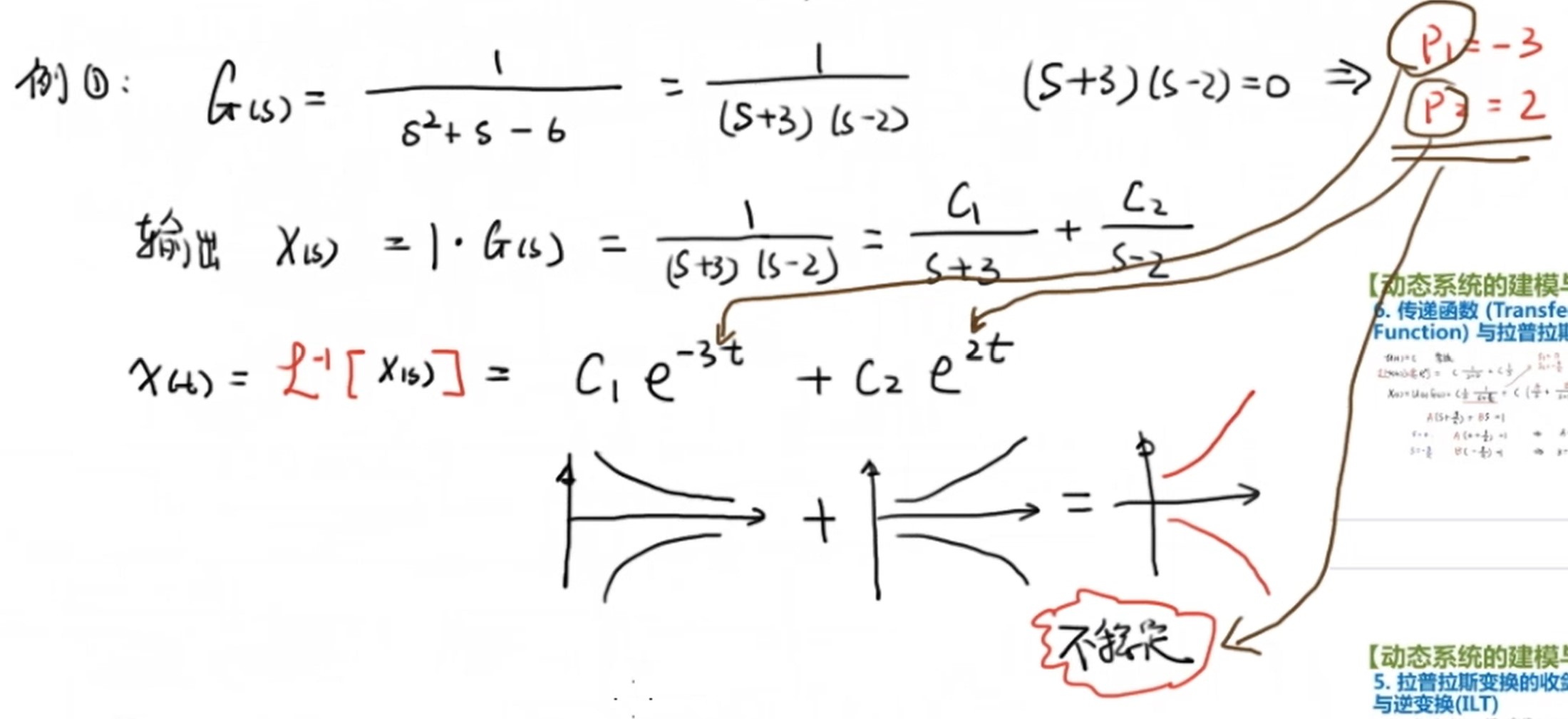
对于一个传递函数(或者说系统的输出,因为在单位冲激下两者相等),我们可以通过因式分解将其拆成基本形式的线性组合,然后对其进行拉普拉斯逆变换可以得到系统输出的时域表达。在这个例子中系统的两个极点分别是-3与2,在时域表达中便是指数函数中时间 (t) 前面的系数。
不难发现随着时间 (t) 趋于正无穷,系统的输出也趋于无穷,因此这是一个不稳定的系统。更具体一点,是2这个极点导致了系统的不稳定,因为 (e^{-3t}) 会在时间 (t) 趋于正无穷时趋于0,而 (e^{2t}) 则为正无穷。
另一个例子,系统的两个基点是共轭复数,通过欧拉公式对于系统输出的时域表达进行化简,可以得到一个振荡的形式。注意到正弦函数系数为 (e^{-t}) ,即时间 (t) 前的系数为-1,因此系统输出将随着时间 (t) 趋于正无穷,振荡着收敛到0,因此这是一个稳定的系统。
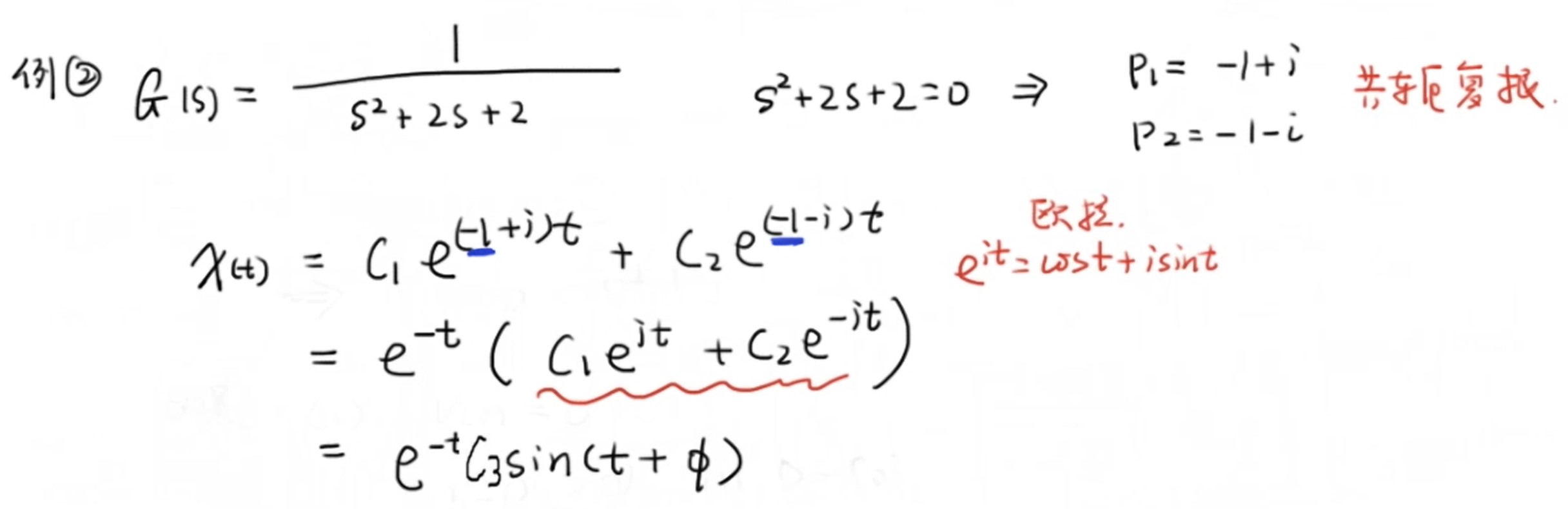
在这种形式下,与上一个例子的规律相同,时间 (t) 前的系数分别为- + 0时,系统的输出会形如以下图像。注意到当系数为0时指数函数的值为1,系统便会保持稳定的震荡。
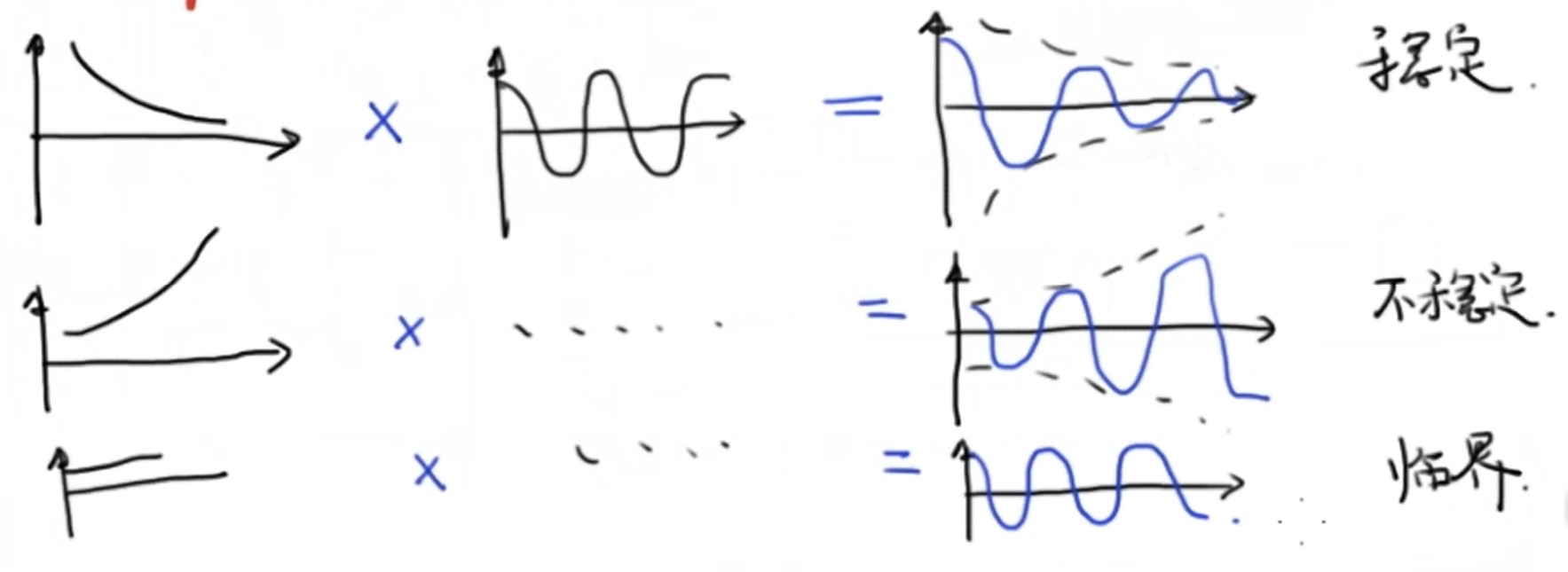
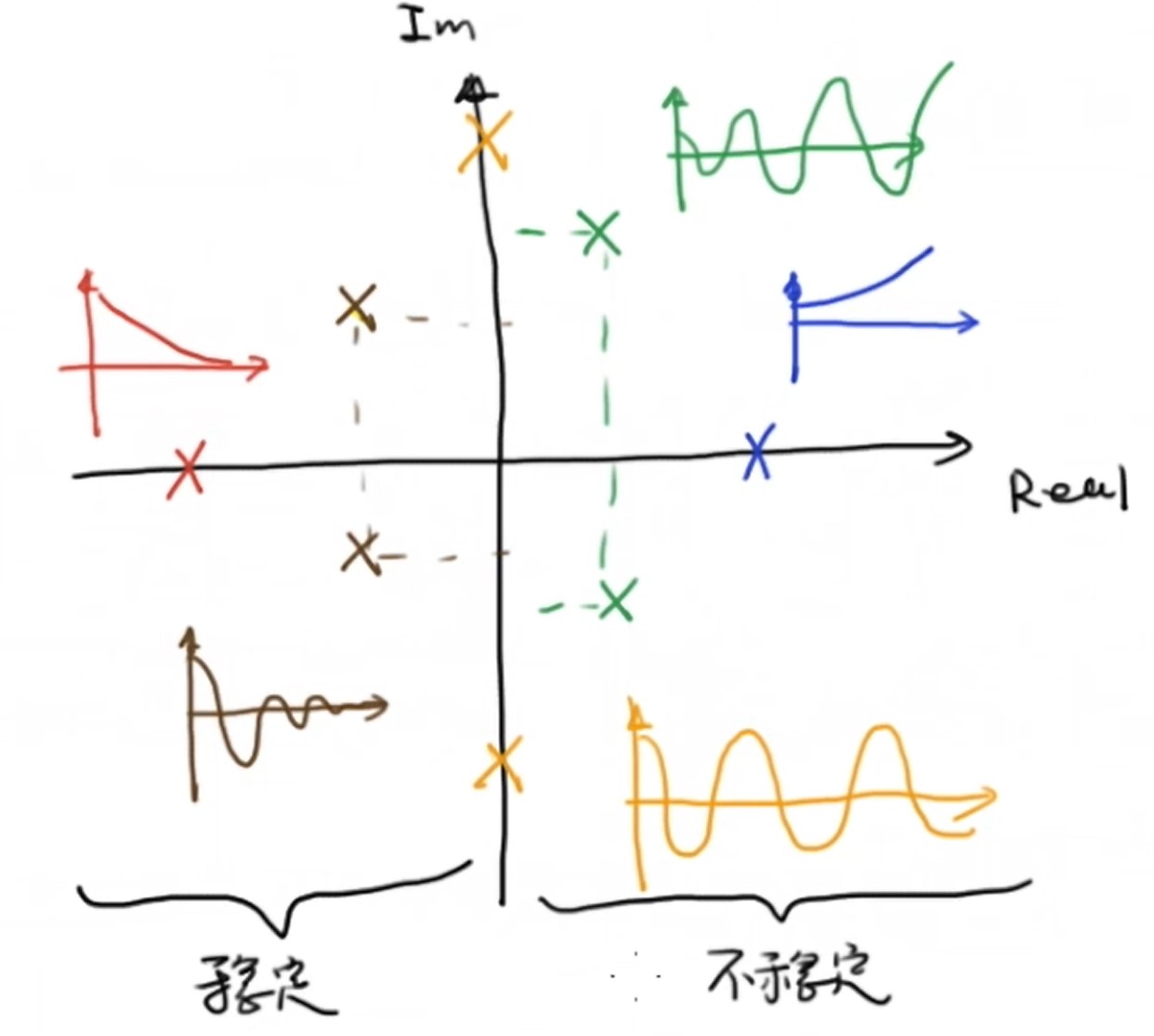
系统的极点画在复平面上,有这么几种情况:
稳定:
- 红色极点实部<0,系统会平滑收敛,
- 褐色极点共轭并且实部<0,系统会振荡收敛
临界稳定:
- 黄色极点共轭并且实部 = 0,系统会无休止的振荡
不稳定:
- 绿色极点共轭并且实部>0,系统会振荡趋于无穷
- 蓝色极点实部>0,系统会平滑趋于无穷
4 总结
有了以上的结论,我们就可以理解经典控制的核心设计思路,即通过设计控制器D,将系统闭环传递函数的零点设计到虚轴左侧,进而让系统达到稳定,这个过程就叫做极点配置。另外的,在现代控制理论中,通过研究状态矩阵的特征值进而分析系统稳定性,特征值便相当于系统的极点。