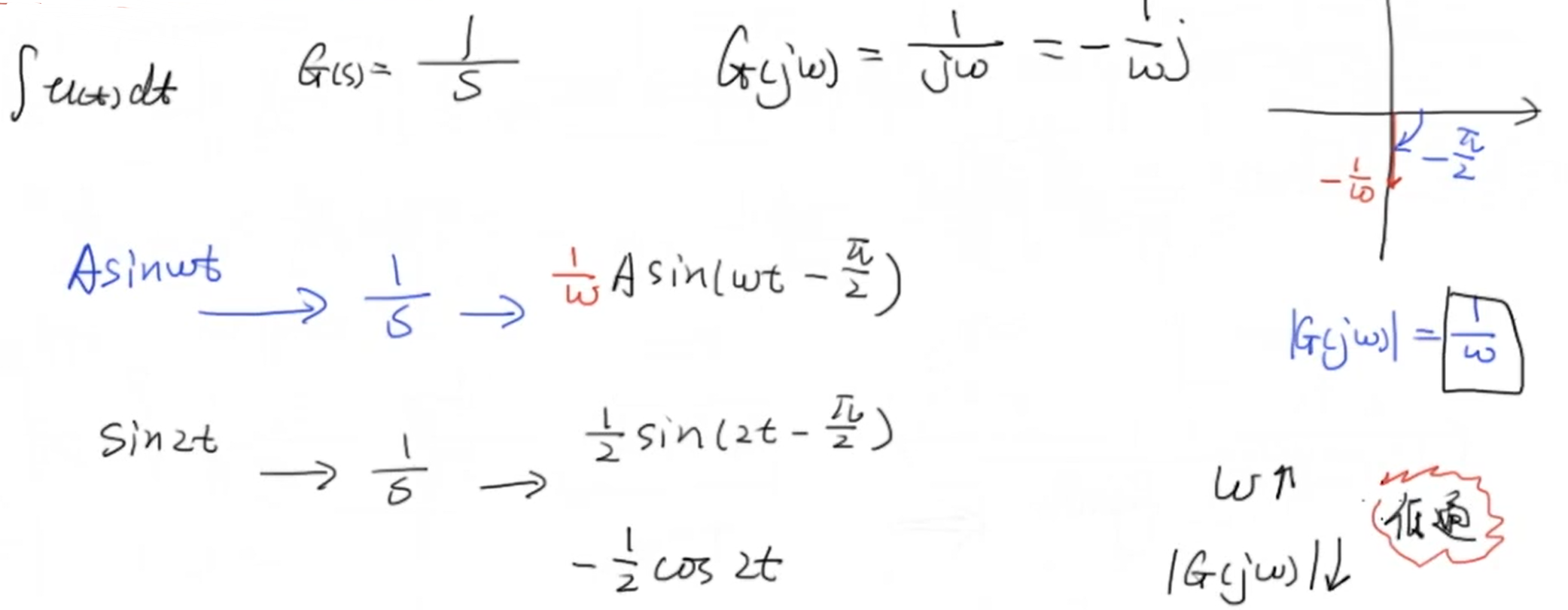该系列为DR_CAN动态系统的建模与分析系列视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 LTI系统对信号的作用
信号经过线性时不变系统后其频率不会发生改变。其幅值与相位的改变分别称为振幅响应(Magnitude Response)和幅角响应(Phase Response)
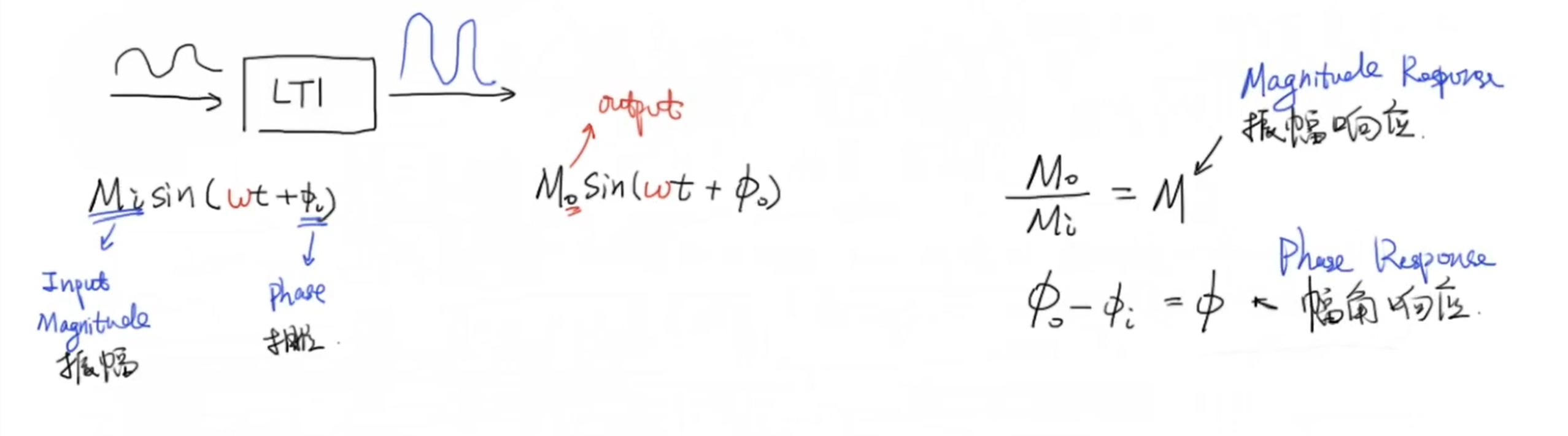
2 频率响应推导过程
一个正弦波的基本形式如下,经过计算合并可以写成 (M_i sin (omega t + phi_i)) 的形式:

对输入信号 (u(t)) 进行拉普拉斯变换可得到 (U(s)) ,另外的,系统传递函数 (G(s)) 也可以对分母进行因式分解写成以下形式:
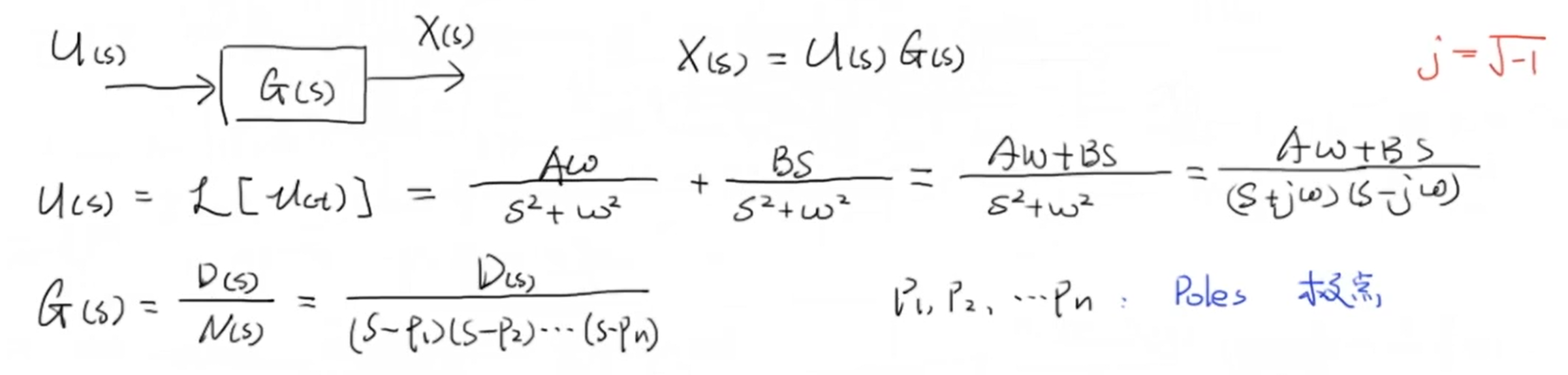
通过 (U(s)) 与 (G(s)) 我们可以计算系统的输出 (X(s)) ,并通过待定系数法拆分成 n+2 项分式。再对其进行合并可以得到这样一长串的表达式,而这一长串分子等于 ((Aomega + Bs)D(s)) :
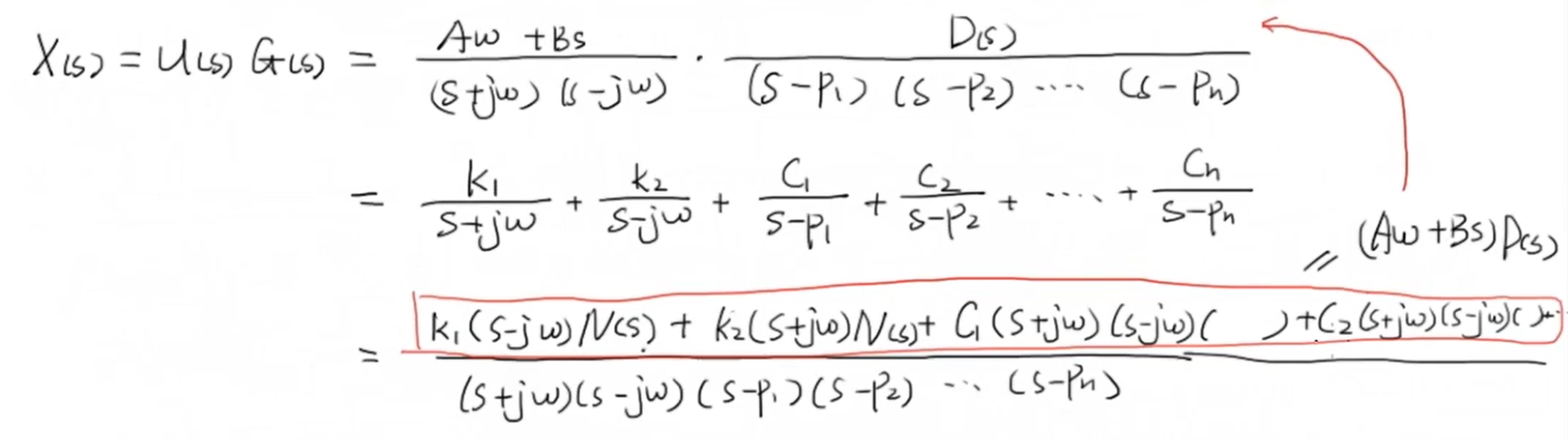
我们对分式表示形式的 (X(s)) 进行拉普拉斯逆变换,可以得到系统输出的时间响应:

对于稳定系统来说,系统极点的实部均小于零,则有 (lim _{t ightarrow infty} C_ne^{P_nt} = 0) ,有这个性质我们可以得到系统输出的稳态(steady state)表示形式:
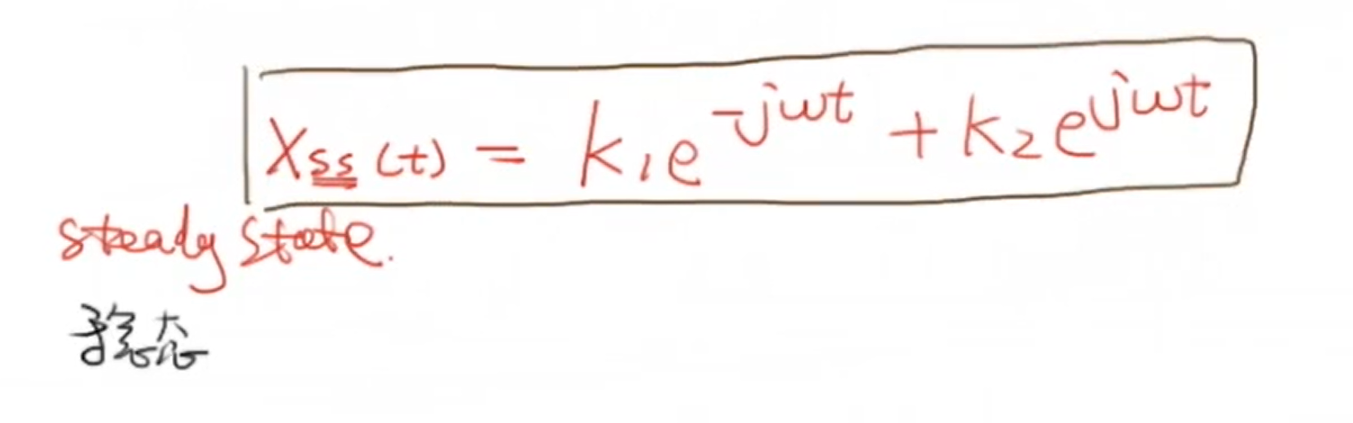
频率响应实际上是一种稳态响应。而现在的问题就变成了求解 (k_1) 和 (k_2) ,通过上面对 (X(s)) 的变形,我们可以构建以下等式并代入特定值求解 (k_1) 和 (k_2) :

另外的,(G(jomega)) 与 (G(-jomega)) 为共轭复数,假设 (G(jomega)) 俯角为 (phi _G) ,则 (G(-jomega)) 俯角为 (-phi _G) ,通过用俯角模长形式改写 (k_1) 和 (k_2) 中的 (G(jomega)) 与 (G(-jomega)) ,并将其代入系统输出稳态表达式中,可得:
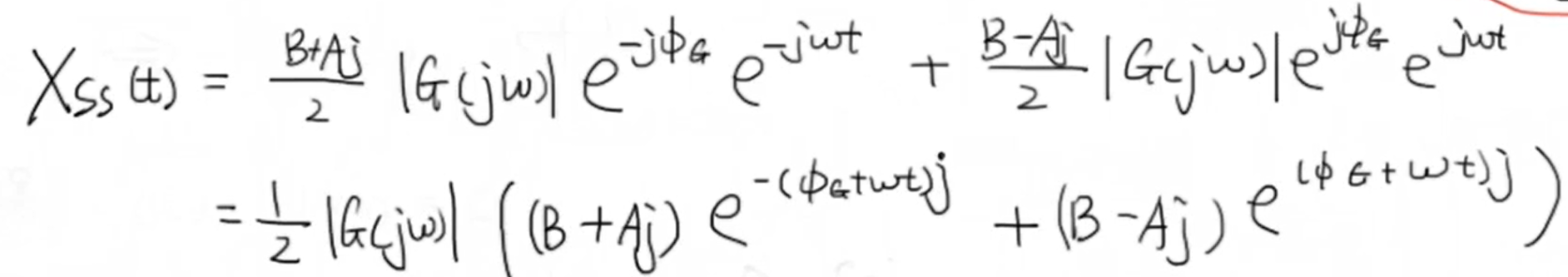
根据欧拉公式,有:
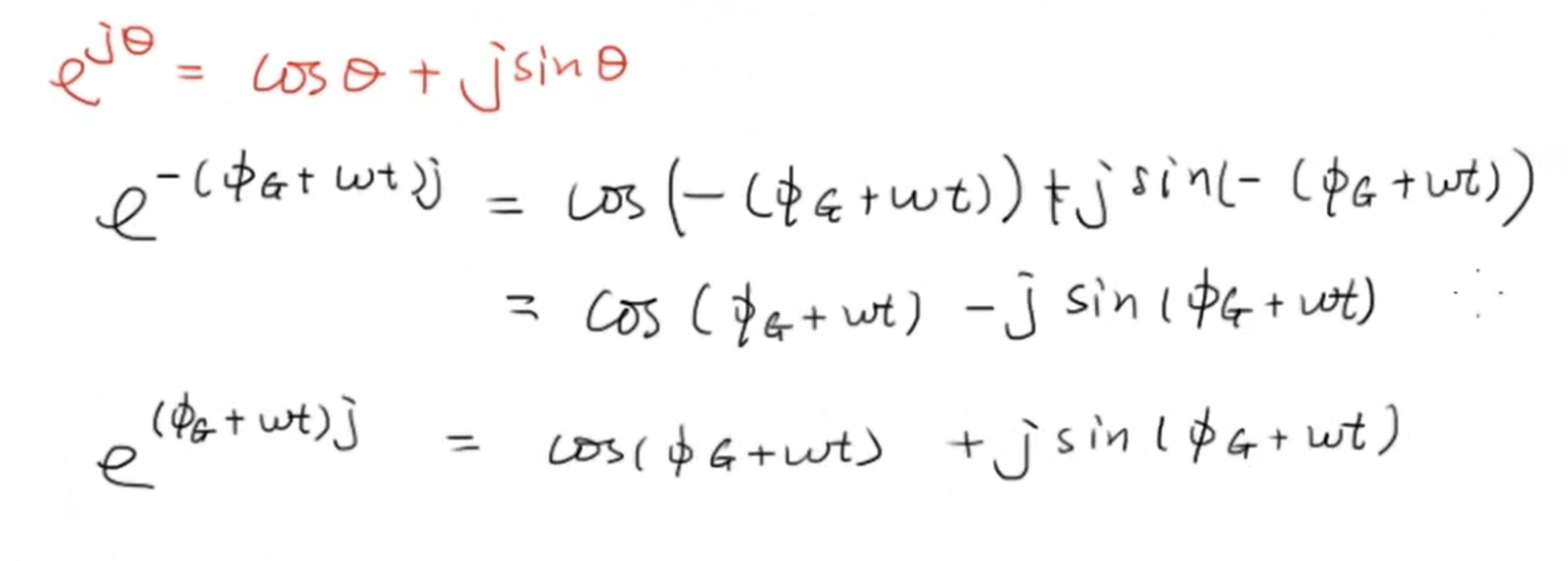
代入 (X_{ss}(t)) 可得:
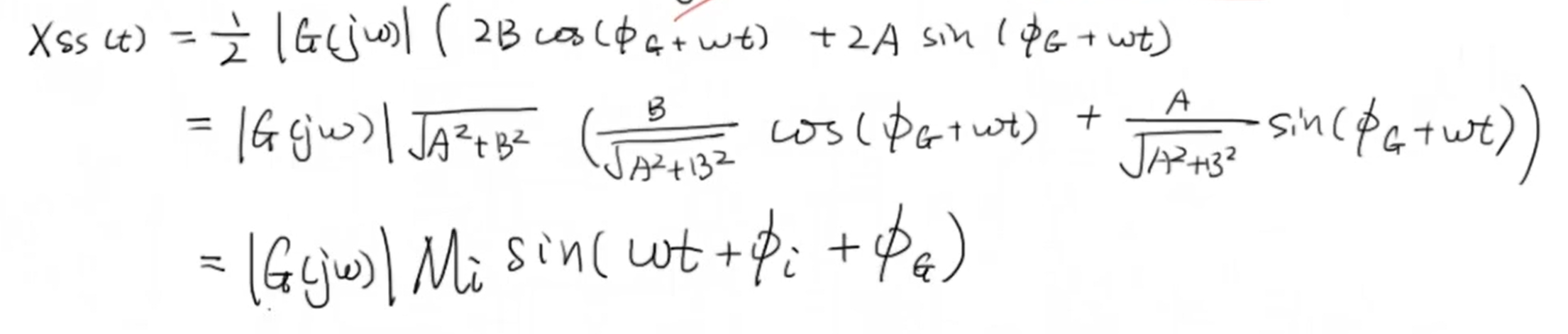
通过以上计算,我们就得到了关于振幅响应和幅角响应的重要结论:
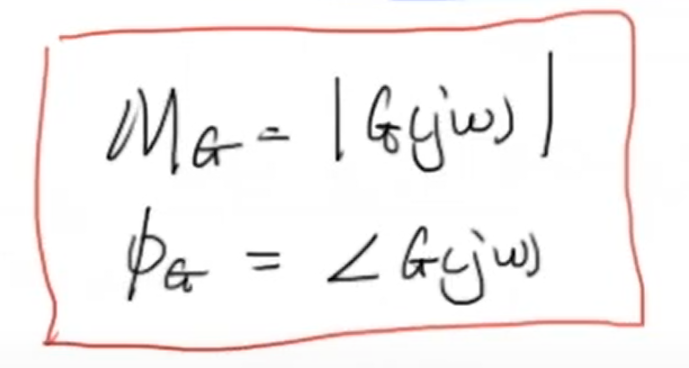
3 一个积分的例子
积分的拉普拉斯变换为 (frac{1}{s}) ,通过代入 (jomega),我们可以求出任意频率下积分的 (G(jomega)) 。根据上面振幅响应和幅角响应的结论,即振幅响应的值为 (G(jomega)) 的幅值,幅角响应的值为 (G(jomega)) 的幅角。
我们便可以根据积分的振幅响应和幅角响应得到这样的结论:一个信号经过积分以后会滞后 (frac{pi}{2}) ,而其幅值则会变为原来的 (frac{1}{omega}) 倍,而 (omega) 为信号的频率,频率越高幅值越小,这也印证了积分的低通滤波性质: