该系列为DR_CAN动态系统的建模与分析系列视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 频率响应
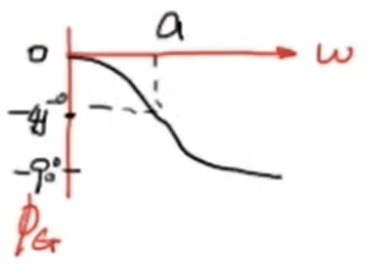
回顾一下频率响应的结论,即振幅响应的值为 (G(jomega)) 的幅值,幅角响应的值为 (G(jomega)) 的幅角:
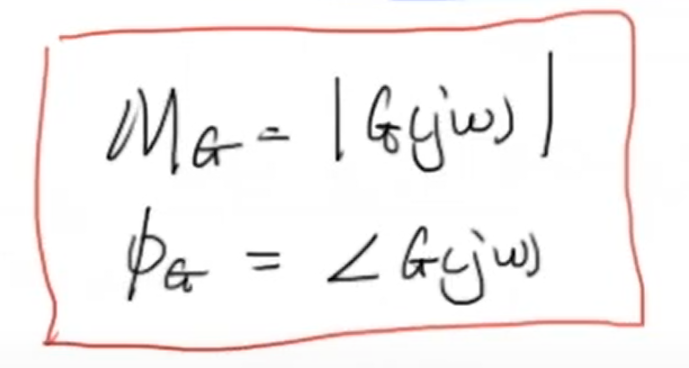
2 一阶系统频率响应
通过代入 (jomega),我们可以求出这个一阶系统的的 (G(jomega)) :
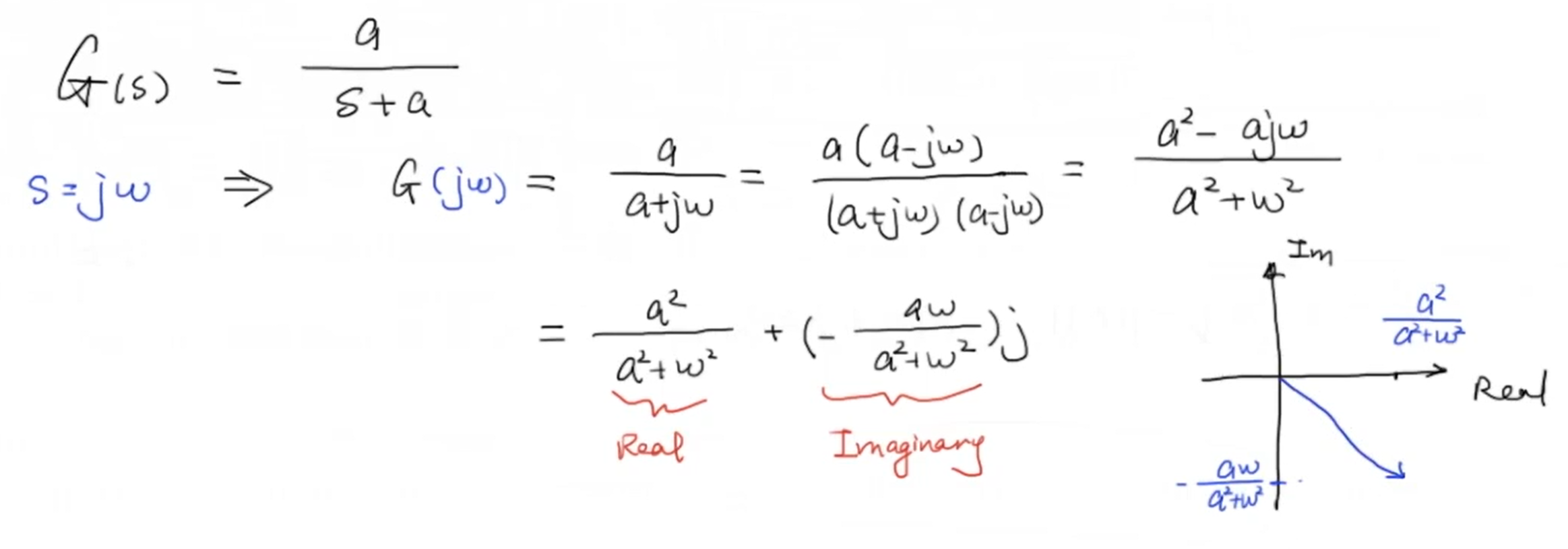
- 振幅响应
通过勾股定理计算其模长并化简,对化简结果进行分析,可以根据 (omega) 的值分为四种情况,可以看出,随着 (omega) 的增大, (G(jomega)) 的值会由1不断减小至0,并且当 (omega=a) 时 (G(jomega)=sqrt{frac{1}{2}}) ,我们称这个 (omega) 为截止频率(Cut-off Frequency)。另外的,若将纵坐标换成 (20 log | G(jomega)|) ,这个图像就成为了伯德图(Bode Plot)其中 (sqrt{frac{1}{2}}) 也就是0.707就变成了-3dB,其对应的 (omega) 就是所谓的系统带宽:
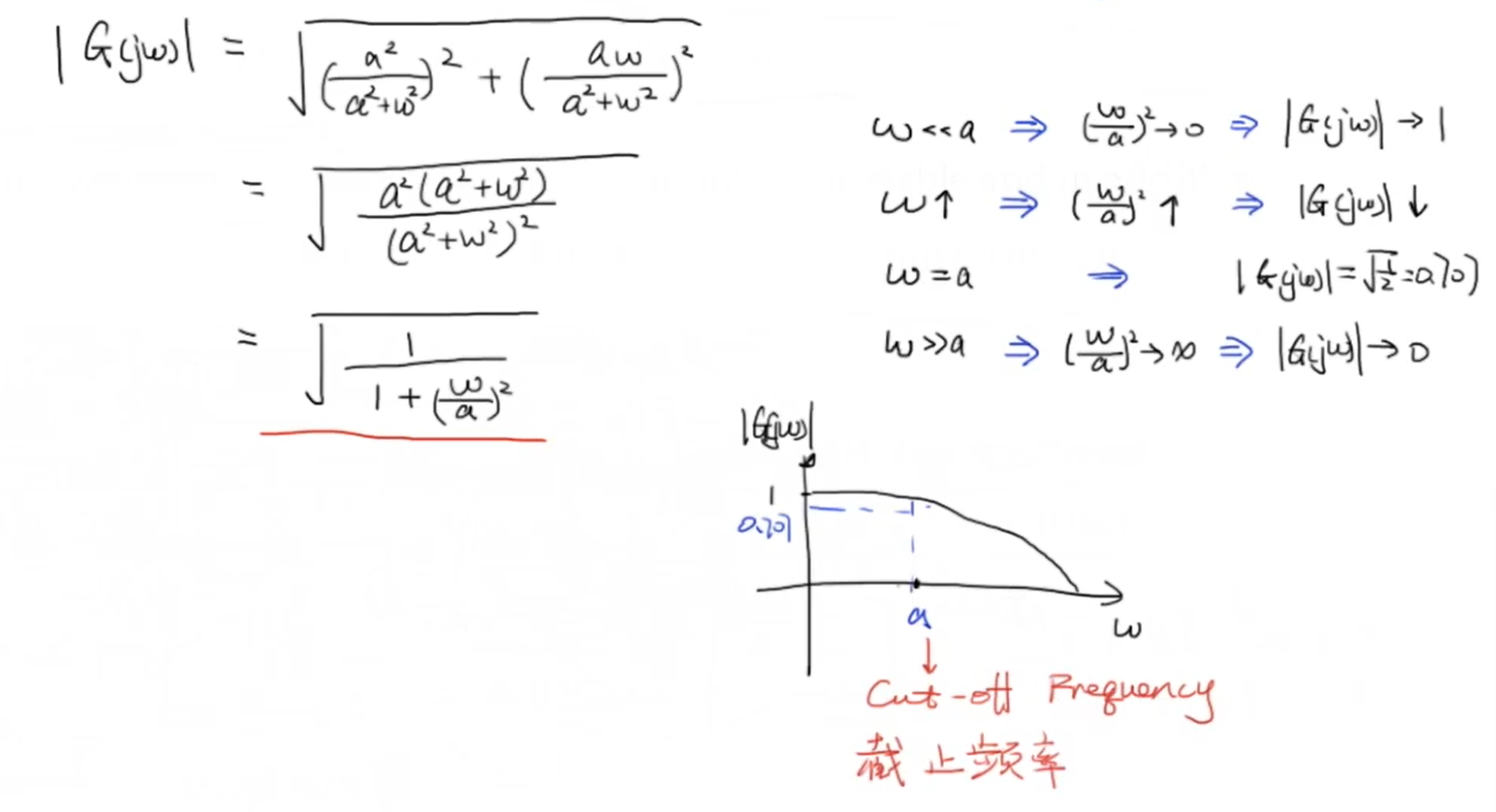
通过振幅响应的图像,我们可以看到,随着 (omega) 的增大, (G(jomega)) 的值会不断减小,所以这就是一个典型的低通滤波器。
在现实生活中有很多这样的例子,比如房间的温度、水池的水位、RC电路等等,都是常见的一阶系统。根据生活经验我们也不难理解他们对高频输入的不敏感。
这些系统有一个共同点,就是他们中都存在一个容器,从数学的角度来讲,这些容器其实就是积分。而积分的拉普拉斯变换为 (frac{1}{s}) ,也正是一个低通滤波器。
从直觉上理解,实际上这些容器提供了一个缓冲,可以对系统的反应带来一定的延迟,从而抵消了高频输入的影响。
- 幅角响应
通过反正切函数我们可以很简单的计算出 (phi_G) :

反映到图像上: