该系列为DR_CAN动态系统的建模与分析系列视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 弹簧阻尼系统的例子
通过对物块 (m) 进行受力分析,并根据牛顿第二定律得到系统的微分方程:
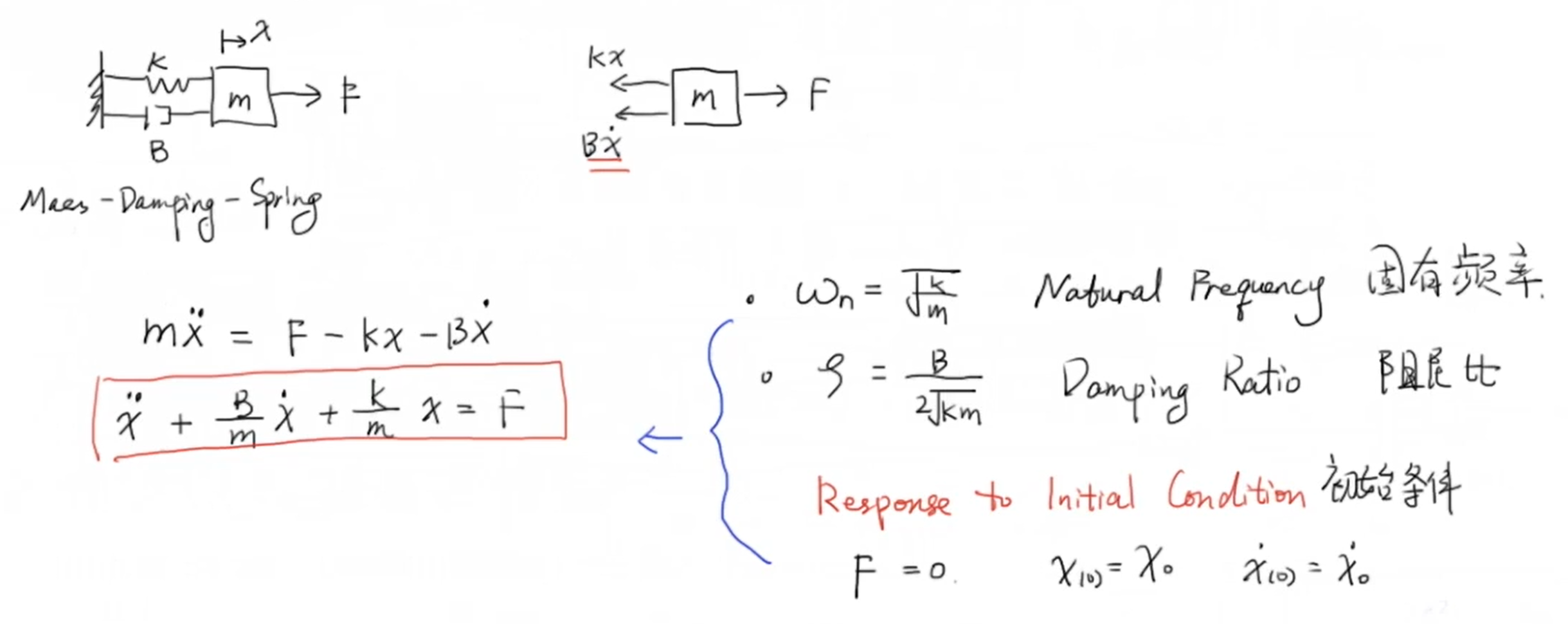
通过定义二阶系统的固有频率(omega) 和阻尼比 (zeta) ,可以将上述微分方程改写为:
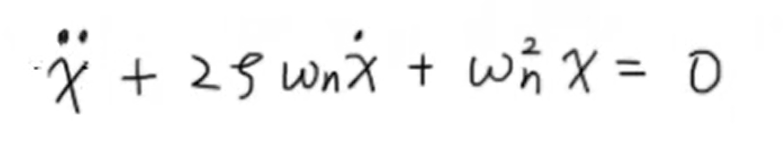
分析这个系统的动态响应实际上就是求解这个微分方程。对于线性齐次微分方程来说,它的解可以由 (x = e^{lambda t}) 这样的形式来表示,将这个形式代入微分方程中,我们可以得到一个普通的代数方程。
通过将公因式 (e^{lambda t}) 提出来,我们就可以得到一个新的形式。由于 (e^{lambda t} eq 0) ,等式两边可以同除 (e^{lambda t}) 消去它,这样一来我们就得到了这个线性齐次微分方程的特征方程,而它的解可以通过求根公式得到。
另外的,特征方程的解也就是 (lambda) 的值便是这个系统的极点,通过对微分方程进行拉普拉斯变换同样可以求得相同的结果:

根据阻尼比 (zeta) 的取值,我们可以分为三种情况:过阻尼、临界阻尼与欠阻尼。其中欠阻尼情况下引入了一个新的定义——阻尼固有频率 (omega_d = omega sqrt{1-zeta^2}) ,通过阻尼固有频率我们可以将 (x(t)) 进一步改写成更直观的形式——一个不断衰减的正弦函数:


一般来说我们常分析以上三种 (zeta>0) 的情况,也就是稳定(可以收敛)的情况。另外的,当 (zetaleq0) 时系统临界稳定或不稳定,根据 (zeta) 的取值还分为三种情况:
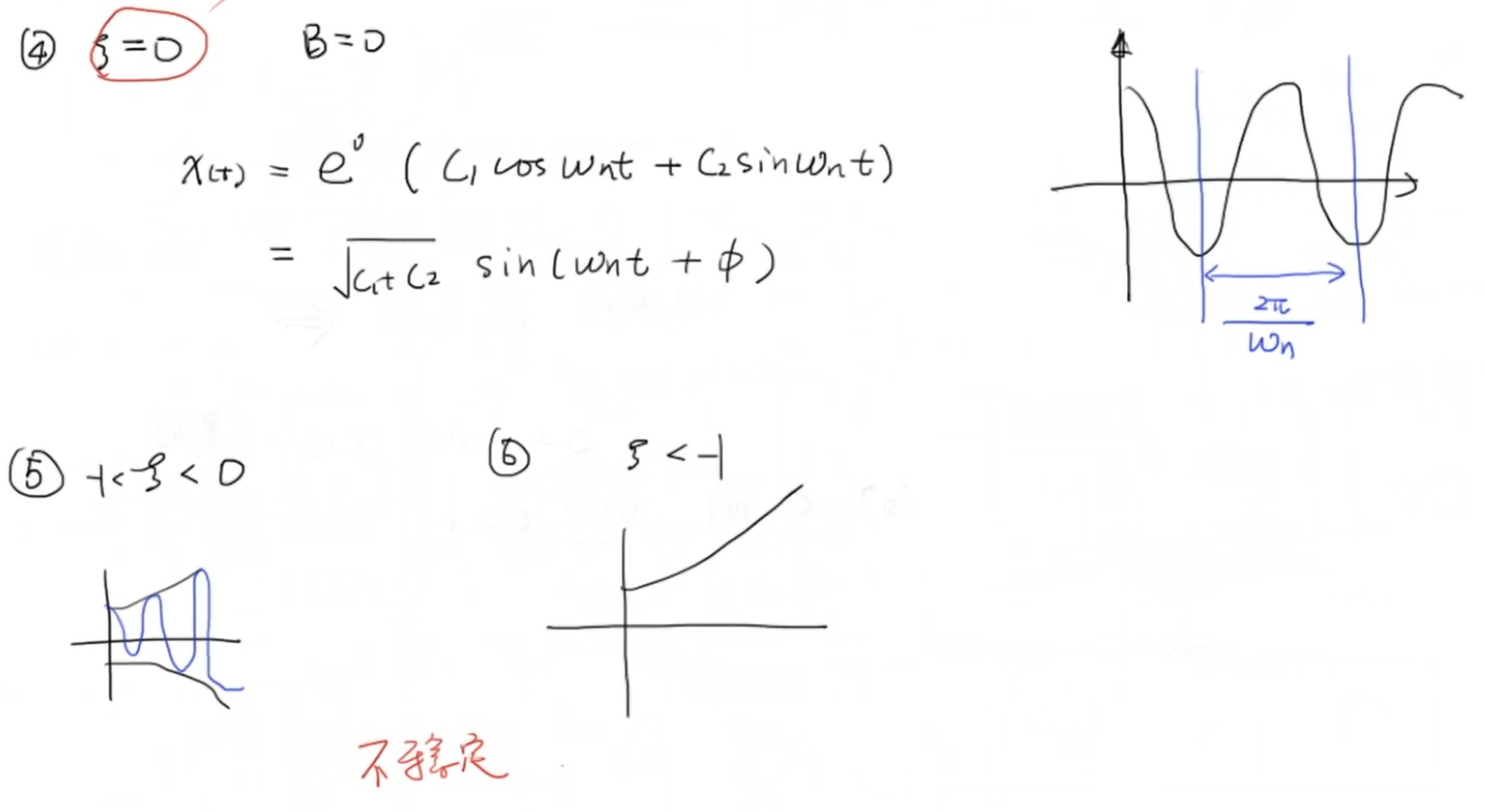
2 在Simulink中进行仿真
通过移项将微分方程表示为 (ddot x = cdotcdotcdotcdot) 的形式,我们就可以在simulink中表示这个微分方程:
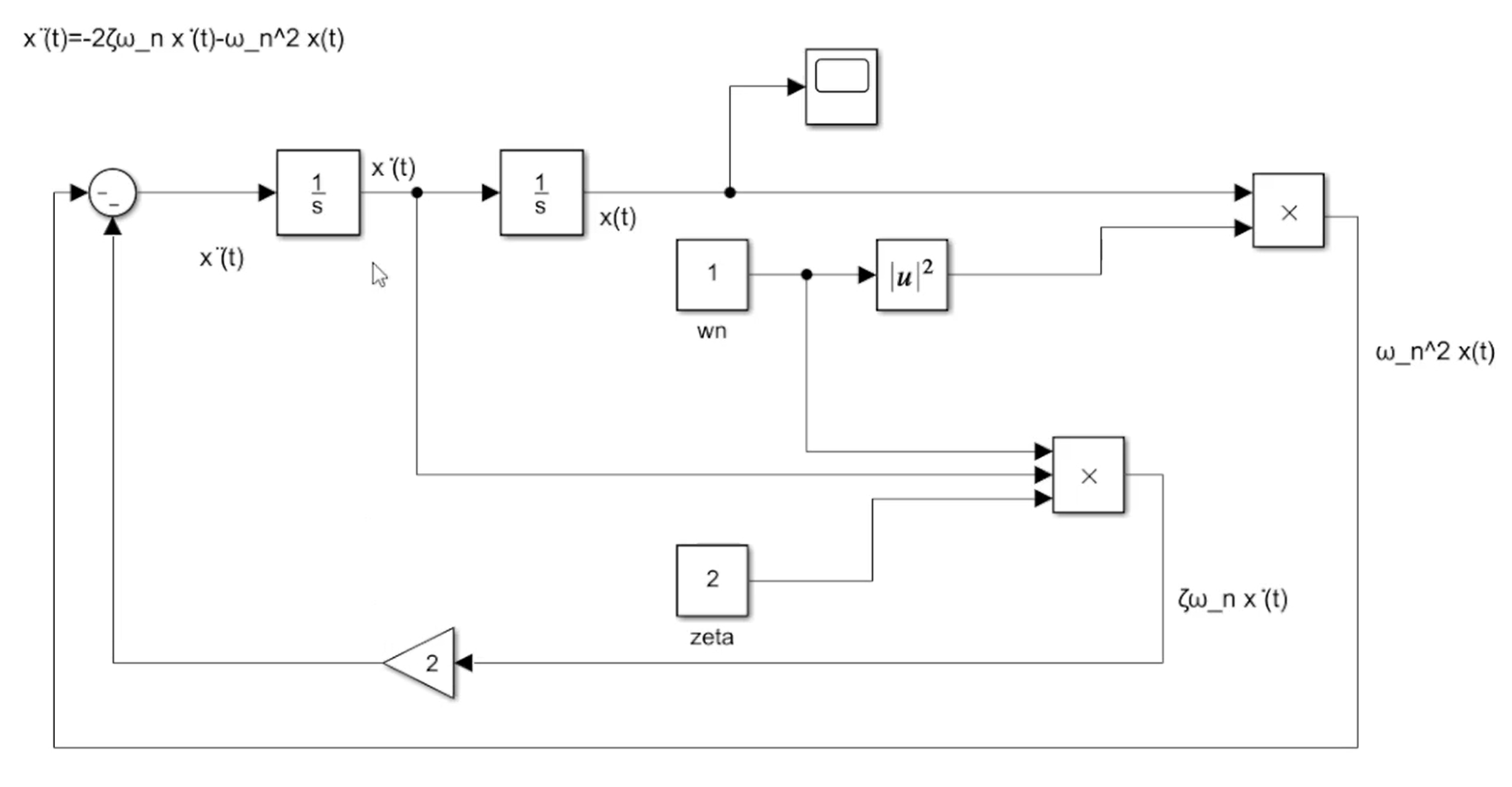
通过改变积分的初始条件以即 (omega) 和 (zeta) 的值,可以得到不同的动态响应,通过scope可以直观了解到 (zeta) 的值对系统动态响应的影响。