这道题目是经典的凸包的最优三角剖分,不过这个题目给的可能不是凸包,所以要提前判定一下是否为凸包,如果是凸包的话才能继续剖分,dp[i][j]表示已经排好序的凸包上的点i->j上被分割成一个个小三角形的最小费用,那么dp[i][j] = min(dp[i][k]+dp[k][j]+cost[i][k]+cost[k][j]),其中,(j >= i+ 3,i+1<=k<=j-1,cost[i][k]为连一条i到k的线的费用)。
上一个图,来自博客http://blog.csdn.net/woshi250hua/article/details/7824433
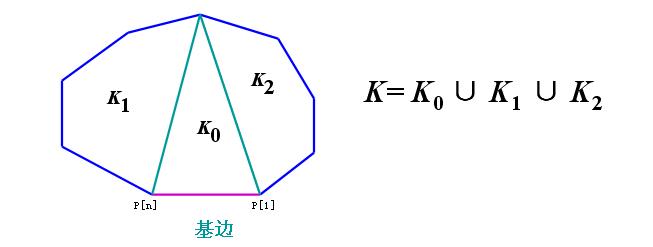
代码如下:

#include <cstdio> #include <iostream> #include <cstring> #include <cmath> #include <cstdlib> #include <algorithm> #define eps 1e-8 using namespace std; typedef long long ll; const int maxn = 500; const int inf = (1 << 30); int dp[maxn][maxn]; int cost[maxn][maxn]; struct point { int x, y; }; point p[maxn], convex[maxn]; bool cmp(const point &p1, const point &p2) { return ((p1.y == p2.y && p1.x < p2.x) || p1.y < p2.y); } int x_multi(const point &p1, const point &p2, const point &p3) { return ((p3.x - p1.x) * (p2.y - p1.y) - (p2.x - p1.x) * (p3.y - p1.y)); } int sgn(double x) { if (fabs(x) < eps) return 0; return x > 0 ? 1 : -1; } void convex_hull(point *p, point *convex, int n, int &len)//求凸包 { sort(p, p + n, cmp); int top = 1; convex[0] = p[0]; convex[1] = p[1]; for (int i = 2; i < n; i++) { while (top > 0 && x_multi(convex[top - 1], convex[top], p[i]) <= 0) top--; convex[++top] = p[i]; } int tmp = top; for (int i = n - 2; i >= 0; i--) { while (top > tmp && x_multi(convex[top - 1], convex[top], p[i]) <= 0) top--; convex[++top] = p[i]; } len = top; } int get_cost(const point &p1, const point &p2, const int &mod) { return (abs(p1.x + p2.x) * abs(p1.y + p2.y)) % mod; } int main() { int n, mod; while (~scanf("%d %d", &n, &mod)) { for (int i = 0; i < n; i++) scanf("%d %d", &p[i].x, &p[i].y); int len; convex_hull(p, convex, n, len); if (len < n)//如果不是凸包的话, puts("I can't cut."); else { memset(cost, 0, sizeof(cost)); for (int i = 0; i < n; i++) for (int j = i + 2; j < n; j++) cost[i][j] = cost[j][i] = get_cost(convex[i], convex[j], mod);//计算处各对角的费用 for (int i = 0; i < n; i++)//初始化dp { for (int j = 0; j < n; j++) dp[i][j] = inf; dp[i][i + 1] = 0; } for (int i = n - 3; i >= 0; i--)//必须逆序,因为dp[i][j] 是由dp[i][k], dp[k][j]推来的,而k是大于i的, for (int j = i + 2; j < n; j++)//同理顺序,因为k小于j for (int k = i + 1; k <= j - 1; k++) dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cost[i][k] + cost[k][j]); printf("%d ", dp[0][n - 1]); } } return 0; }
