剑指Offer_#13_机器人的运动范围

剑指Offer_#13_机器人的运动范围

剑指offer

Contents

• • 题目
  • 思路分析
  • 解答
  • 复杂度分析
  • 解答2

题目

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：
输入：m = 2, n = 3, k = 1
输出：3

示例 2：
输入：m = 3, n = 1, k = 0
输出：1

提示：
1 <= n,m <= 100
0 <= k <= 20

思路分析

这道题使用深度优先搜索（Depth First Search）解决。
具体来说，就是从（0，0）坐标开始，向上，下，左，右四个方向遍历所有可达元素，并进行计数。
特殊的一点是，通过枚举一些测试用例可以观察到，无论如何，其实仅仅需要向下和向右遍历，就可以覆盖所有可达位置。见如下图解，引用自Krahets' Blog。

图解

算法伪代码
采用递归算法，需要确定 递归终止条件 ，以及 递推过程 ，回溯返回值 三个要素。

1. 递归终止条件
   行列索引越界 或 不可达 或 已被访问过，直接返回0
2. 递推过程（dfs过程）
   • 标记当前单元格：使用一个矩阵，将当前访问过的（i，j）坐标元素标为1，避免重复访问。
   • 搜索下一单元格：向下或者向右移动，计算移动后的数位和，调用子递归函数。
3. 回溯返回值
   返回 1 + dfs(i+1,j) + dfs(i,j+1)
   1是出发点位置，也要计算在内
   dfs(i+1,j) 是向下一个单元格的所有可达位置总数
   dfs(i,j+1) 是向右一个单元格的所有可达位置总数

数位之和计算
通过枚举，观察可得道数位和的递推规律，设当前数字为x,有：

• 若 x+1 % 10 == 0,x+1的数位和比x的数位和减少8
• 否则，x+1的数位和比x的数位和增加1

利用这个规律，可以用于计算向下一个元素和向右一个元素的数位和。

解答

class Solution {
    int m,n,k;
    boolean[][] visited;
    public int movingCount(int m, int n, int k) {
        this.m = m;this.n = n;this.k = k;
        this.visited = new boolean[m][n];
        return dfs(0,0,0,0);
    }
    public int dfs(int i,int j,int si,int sj){
        //行列索引越界 或 不可达 或 已被访问过，直接返回0
        if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
        visited[i][j] = true;
        return 1 + dfs(i + 1, j, nextBitSum(si, i), sj)//向下移动
               + dfs(i, j + 1, si, nextBitSum(sj, j));//向右移动
    }

    public int nextBitSum(int curBitSum,int curNumber){//向下或者向右移动时，根据地推公式计算位和
        return (curNumber + 1) % 10 != 0 ? curBitSum + 1:curBitSum -8;//位和的递推公式
    }
}

复杂度分析

时间复杂度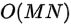
空间复杂度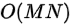

解答2

第二遍做的时候，对于数位和，我想可以直接计算而不使用递推公式，试了一下这样做一样是可以过的，但是这可能就涉及到一些重复计算了。和爬楼梯一题类似，如果你每次都重新计算位和，可能会多几步运算。
因为：

• 如果是直接采用递推公式，只需要判断一下是否是10的倍数，然后直接加一或者减8，是一次加减运算；
• 如果是直接计算，那么对于两位数来说，需要两轮循环，就是两个加减运算。由于这里的行列都限制在100内，所以影响不那么大。

所以最好还是使用第一种办法，用递推公式计算数位和，如果没有观察出来递推规律的话，直接计算也不是不行。

class Solution {
    int m,n,k;
    boolean[][] visited;//相当于把m,n,k和visited设置为全局变量，无需通过参数传递
    public int movingCount(int m, int n, int k) {
        this.m = m;this.n = n;this.k = k;
        visited = new boolean[m][n];//需要实例化
        return dfs(0,0);
    }

    public int dfs(int i,int j){//（i,j）是搜索起始点的坐标
        if(i >= m || j >= n || bitSum(i) + bitSum(j) > k || visited[i][j] == true) return 0;
        visited[i][j] = true;//这里是否需要加this.呢？加不加都可以。
        return 1 + dfs(i + 1,j) + dfs(i, j + 1);
    }

    public int bitSum(int x){
        int sum = 0;
        while(x != 0){
            sum += x % 10;//sum加上当前位数字
            x = x / 10;//移位，去除最后一位数字
        }  
        return sum;
    }
}