剑指Offer_#14-2_剪绳子

剑指Offer_#14-2_剪绳子

剑指offer

Contents

• • 题目
  • 思路分析
    • 求余运算和求模运算的区别
    • java,python中的取余和取模运算
  • 题解1
    • 复杂度分析
  • 题解2
    • 复杂度分析

题目

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m] 。请问k[0]*k[1]*...*k[m] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
 
提示：
2 <= n <= 1000

思路分析

和前一题相比，唯一的区别就是这里的输入范围变大的，所以导致最后的结果可能会超过int所表示的最大范围，所以需要考虑如何求这个大数的余数。
需要注意的是，求余和求模并不完全相同。 由于此题当中涉及到的被除数和除数都是正整数，所以求余和求模运算结果相同，但是如果除数和被除数的符号不同，那么求余和求模的结果不是相同的。
关于大数求余，其实更像一个数学问题，需要先理解数学推导，才能写出正确代码。

求余运算和求模运算的区别

通常取模运算也叫取余运算，它们返回结果都是余数 ,rem 和 mod 唯一的区别在于:

• 当 x 和 y 的正负号一样的时候，两个函数结果是等同的；
• 当 x 和 y 的符号不同时，rem 函数结果的符号和 x 的一样，而 mod 和 y 一样。

具体是因为这两个函数的实现机制不同
对于整数 a，b 来说，取模运算或者求余运算的方法要分如下两步：
1、求整数商：c=a/b
2、计算模或者余数：r=a-(c*b)
求模运算和求余运算在第一步不同
取余运算在计算商值向0方向舍弃小数位
取模运算在计算商值向负无穷方向舍弃小数位
例如：4/(-3) 约等于 -1.3
在取余运算时候商值向 0 方向舍弃小数位为 -1
在取模运算时商值向负无穷方向舍弃小数位为-2
所以
4rem(-3)=1 4mod(-3)=-2

java,python中的取余和取模运算

• 在java中，%是取余运算，英文是remainder；Math.floorMod()是取模运算。
  • 大部分编程语言中%结果与被除数同符号。都是这样，比如C,Go，C#，Java，Rust，Swift，JavaScript，PHP。
• 在python中，%是取模运算，英文是modulus；math.fmod是取余运算。
  • python中，%运算结果与除数同符号，所以与java是相反的。

题解1

这是快速幂取余算法。
理解快速幂取余算法，首先需要理解快速幂算法（参考加速幂运算 | 一瓜算法小册），快速幂取余算法是快速幂算法的一个扩展，仅仅是在迭代过程中增加了一个取余操作。
与循环求余相比，循环求余每次迭代时指数增加1，而快速幂求余每次迭代时指数变为原来的2倍，所以迭代次数变为对数级。
具体原理可参考快速幂取模算法 | 一瓜算法小册，篇幅较长，不再赘述。

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n-1;
        int b = n % 3,p = 1000000007;
        long rem = 1,x = 3;
        for(int a = n/3 - 1;a > 0;a /= 2){//a的初始值为什么是n/3-1?这是长度为3的绳子段数-1。循环过程就是计算3^(a-1)%p。
            if(a % 2 == 1) rem = (rem * x) % p;//逢奇数，需要特殊处理
            x = (x * x) % p;
        }
        if(b == 0) return (int)(rem * 3 % p);//3^a%p
        if(b == 1) return (int)(rem * 4 % p);//3^(a-1)*4%p
        return (int)(rem * 6 % p);//b==2时，3^a*2%p
    }
}

复杂度分析

由于每次指数减小一倍，时间复杂度是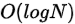

题解2

贪心算法，也就是直接分析出每一次都是剪下长度为3的绳子最好，所以直接通过循环模拟这个过程，每次绳子长度减小3，结果乘以3。
循环结束的结果分为三种：
1.n=2，等于说无限除以3，最后余下绳子长度为2，此时将res乘以2即可
2.n=3，绳子全部用完，直接所有3相乘即可
3.n=4，等于说余下绳子长度为1，因为4%3=1，但是3<2*2，也就是4本身，故最后乘4
这里的求余方式是循环求余算法，复杂度稍高，但是更加直观。
循环求余法的依据是如下公式（同余定理），其中的代表求余运算

也就是说，每一轮都进行一次求余操作，再迭代，和先迭代完成后再进行求余操作，结果相同。

class Solution {
    public int cuttingRope(int n) {
        if(n<=3) return n-1;
        long res=1;
        while(n>4){
            res*=3;
            res=res%1000000007;
            n-=3;
        }
        return (int)(res*n%1000000007);
    }
}

复杂度分析

相比二分求余法，这个方法的复杂度稍高，是