剑指Offer_#17_打印从1到最大的n位数
Contents
题目
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
示例 1:
输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]
说明:
用返回一个整数列表来代替打印
n 为正整数
思路分析
leetcode上面这一题的题意与书本上的原意不符,书中这一题的考察重点是大数问题,即如果输入的数字位数n很大,表示的n位数字可能超出int的表示范围。但leetcode上面规定的返回值类型是int数组,那么相当于直接忽略了大数问题。
所以,在解答中,分为两个思路来做,
- 第一种是直接不考虑大数问题,目标是能通过leetcode的测试;
- 第二种是按照书上题意,还得考虑大数问题的存在。
思路1很简单,不详细写了。
对于思路2,其实也还分为两种方法:
- 字符'0'~'9'进行n位的全排列,即可得到所有的数字
- 用字符串表示数字,并模拟数字相加,进位的过程
方法1:字符全排列(考虑大数问题)
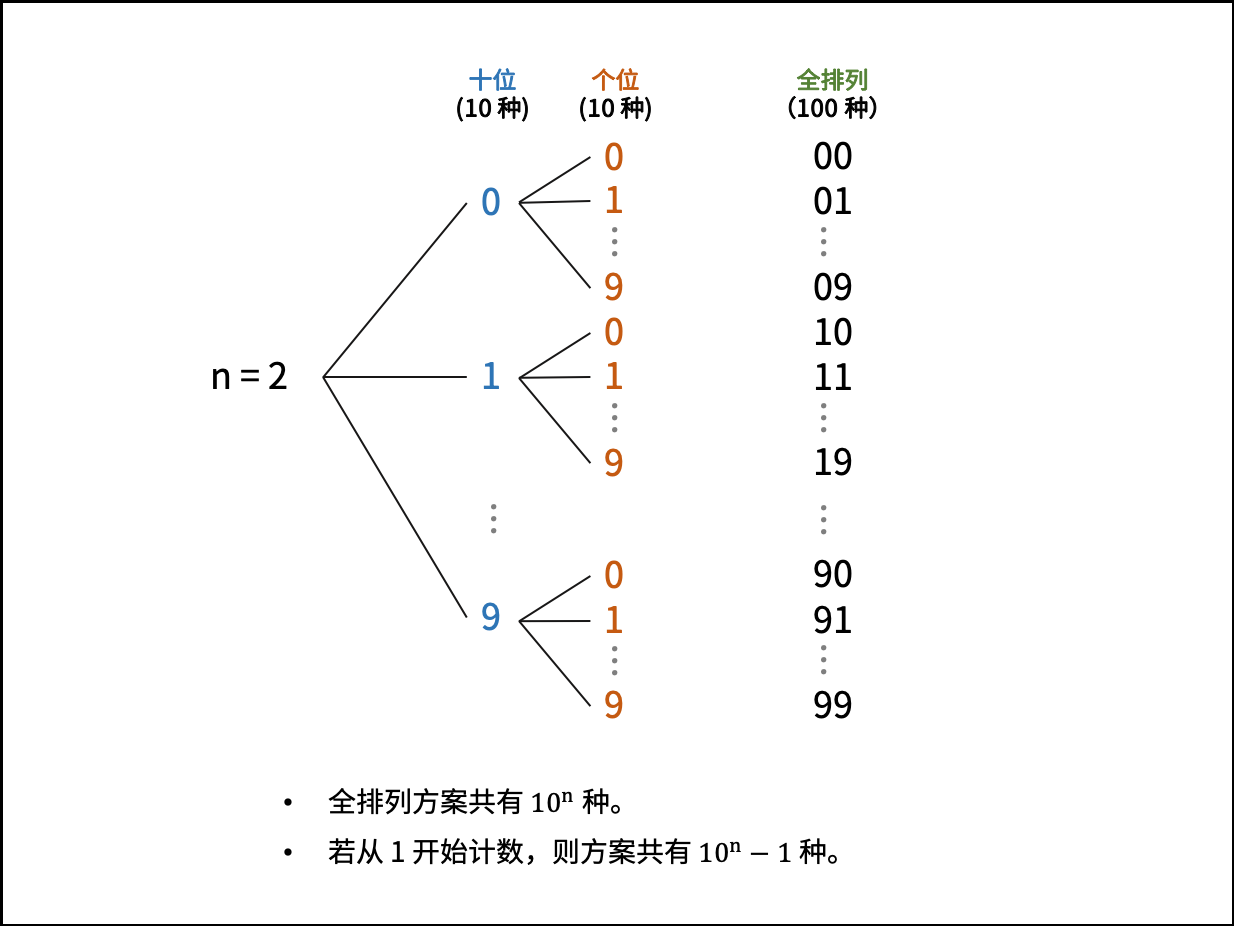
如下图所示,可以从最高位到最低位进行排列组合,将各种组合情况画成一个树的形式,那么打印所有数字的工作可以转化为对这棵树的深度优先遍历,每次遍历的路径,就是一个数字。
算法流程
- 开始时,start == 1.固定第1位数字为0,遍历第2位数字,即得到"00"-"09",去除前边的0,append进入res
- 遇到"09"时,nine更新为1,start更新为0
- "00"-"09"结束后,回溯到第一位数字,nine还原为0.固定第1位数字为1,遍历第二位数字,即得到"10"-"19",append进入res
- 遇到"19"时,nine更新为1
- "10"-"19"结束后,回溯到第一位数字,nine还原为0.固定第1位数字为2,遍历第二位数字,即得到"20"-"29",append进入res
依次类推...... - 遇到"99"时,nine更新为2。循环结束,返回从1到99的字符串
方法2:用字符串表示数字,模拟数字加法
算法流程
- 数字加1时,个位数增加1,如果个位数加1后大于10,则向更高位进位
- 依次类推,从后往前遍历表示数字的字符串,在每一位数字上判断是否会进位(如果数字末尾是连续的9,那么会发生连续进位,比如199+1=200,会连续在个位和十位上进位)
- 每次数字加1,完成所有进位操作之后,将本数字添加到res末尾
- 添加数字之前,需要数字的第一个字符开始遍历,找到第一个非'0'字符的索引,去除数字前半部分补位的'0'
- 如果最高位数字发生进位,超过10,那么说明已经到了n位数字能表示的最大值,添加数字到res的循环停止,返回res即可。
解答1:循环打印(不考虑大数问题)
class Solution {
public int[] printNumbers(int n) {
int max = (int)Math.pow(10,n);//注意这里必须进行类型转换,加上(int)
int[] res = new int[max - 1];
for(int i = 1;i <= max - 1;i++){
res[i - 1] = i;
}
return res;
}
}解答2:字符全排列(考虑大数问题)
public class Solution {
StringBuilder res;//StringBuilder支持不断对字符串进行修改,且不会产生新的对象
int nine = 0,start,n;//start是左边界
char[] num, loop = {'0','1','2','3','4','5','6','7','8','9'};
public String printNumbers(int n){
this.n = n;//设置为类变量,递归函数也可以访问
res = new StringBuilder();
num = new char[n];//数组定义必须给出长度
start = n - 1;//个位数,左边界为数字位数-1
dfs(0);
res.deleteCharAt(res.length() - 1);//删除最后一个逗号
return res.toString();
}
void dfs(int x) {
if (x == n) {
String s = String.valueOf(num).substring(start);//将num的有效位取出(舍去开始的0)
if(!s.equals("0")) res.append(s + ",");//舍去第一个“0”
if(n - start == nine) start--;//nine是遍历过程中,遇到9的个数;start--说明进位了
return;
}
for(char i:loop){
if(i == '9') nine++;
num[x] = i;//第x位数字,分别取值0~9
dfs(x + 1);//第x位数字固定位0~9中任意一个,然后继续遍历x+1位数字
}
//第x位数字全部遍历结束,回溯到第函数dfs(x-1),之前nine++是因为在第x位遇到了9。
//现在回到的x-1位,第x位遇到的9不算了,所以nine要恢复到原本的值,即nine--;
nine--;
}
}注意: 此代码无法在leetcode上通过,因为这里返回的是字符串数组,而非leetcode要求的int数组,所以只能在本地IDE自行测试。
解答3:字符串表示数字(考虑大数问题)
通过字符串表示数字,模拟数字加法。
数字加法的要点就是逢10进位,进位操作从后向前。
如果第一位数字发生进位变为1,说明达到了n位数字表示的最大值。
public class Solution{
ArrayList<String> res;
char[] number;
int n;//数字位数
public ArrayList<String> print1ToMaxOfNDigits(int n){
this.n = n;
res = new ArrayList<String>();
number = new char[n];
for(int i = 0;i <= n - 1;i++){
number[i] = '0';
}
while(!Increment()){
AppendToRes();
}
return res;
}
public boolean Increment(){
boolean isOverflow = false;
int nTakeOver = 0;
for(int i = n - 1;i >= 0;i --){//执行加一操作,分为进位和不进位分别处理
int nSum = (int)(number[i] - '0') + nTakeOver;//本位数字加上进位的和
if(i == n - 1) nSum ++;//数字加1,先加在个位数字上,其他位的变化都是进位导致的
if(nSum >= 10){//nSum >= 10,说明发生进位了
if(i == 0) isOverflow = true;//进位发生在最高位,说明已经到了最高位
else{//进位发生在其他位,则进行进位操作
nSum -= 10;//本位数字减10
nTakeOver = 1;//记录进位,下轮循环开始时会加到下一位
number[i] = (char)('0' + nSum);
}
}else{//没有发生进位,那么就可以跳出循环了
number[i] = (char)('0' + nSum);
break;
}
}
return isOverflow;
}
public void AppendToRes(){
int notBegining0Index = 0;
for(int i = 0;i <= n - 1;i ++){
if(number[i] != '0'){
notBegining0Index = i;
break;
}
}
String s = String.valueOf(number).substring(notBegining0Index);
if(!s.equals("0")) res.add(s);//将当前数字添加到末尾
}
}注意: 此代码无法在leetcode上通过,因为这里返回的是字符串数组列表,而非leetcode要求的int数组,所以只能在本地IDE自行测试。
