剑指Offer_#55

剑指Offer_#55 - I_二叉树的深度

剑指offer

Contents

• • 题目
  • 思路分析
    • 方法1：自底向上
    • 方法2：自顶向下
  • 解答
    • 解答1：自底向上
    • 解答2：自顶向下

题目

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，
    3
   / 
  9  20
    /  
   15   7
返回它的最大深度 3 。

提示：
节点总数 <= 10000

思路分析

方法1：自底向上

求整棵树的深度这个问题，可以分解为求当前节点左右子树深度的子问题，即存在递推关系：

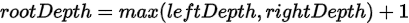
所以可以用递归解决。
终止条件：
当前访问到节点是null,深度看作0。
递推过程：

• 求左右子树深度leftDepth,rightDepth。
• 

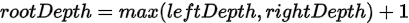
自底向上的递推是通过递归函数的返回值传递信息，即把max(leftDepth,rightDepth) + 1用返回值返回到父递归函数。

方法2：自顶向下

与自底向上的思路不同，自顶向下的思路是相反的。

• 自底向上：先得出左右子树的深度，再得出根节点的树的深度。
• 自顶向下：先得出根节点的层数，再得出根节点左右子树所在的层数。

自顶向下的递推需要通过函数参数来传递信息，即把当前节点的深度+1用参数传递给子递归函数。

解答

解答1：自底向上

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth,rightDepth) + 1;
    }
}

解答2：自顶向下

class Solution {
    private int maxDepth = 0;
    public int maxDepth(TreeNode root) {
        recur(root, 1);
        return maxDepth;
    }
    private void recur(TreeNode root,int depth){
        //如果是null,终止递归
        if(root == null) return;
        //如果root是叶子节点，更新最大值
        if(root.left == null && root.right == null)
            maxDepth = Math.max(maxDepth,depth);
        //向下递推，需要给出depth参数
        recur(root.left,depth + 1);
        recur(root.right,depth + 1);
    }
}