LeetCode Notes_#622_设计循环队列

LeetCode Notes_#622_设计循环队列

Contents

• • 题目
  • 思路分析
  • 解答
    • 复杂度分析

题目

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

提示：
所有的值都在 0 至 1000 的范围内；
操作数将在 1 至 1000 的范围内；
请不要使用内置的队列库。

思路分析

首先思考需要哪些类变量（实例字段）?

• queue:数组，用于存放队列元素
• capacity:队列最大容量
• count:队列当前元素数量
• headIndex:队头元素在数组中的位置

然后思考每个函数（对数据结构的各种操作）如何实现？

两个关键点

1. 入队之前先判断队列是否满了，出队之前判断队列是否为空
2. tailIndex的计算公式：
   
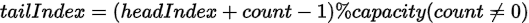
   关键就在于求余操作，求余实现了循环。

解答

class MyCircularQueue {
    int[] queue;//存储元素的数组
    int capacity;//队列长度
    int count;//表示当前元素的个数
    int headIndex;//当前的第一个元素
    
    /** Initialize your data structure here. Set the size of the queue to be k. */
    public MyCircularQueue(int k) {
        capacity = k;
        queue = new int[capacity];
        count = 0;
        headIndex = 0;
    }
    
    /** Insert an element into the circular queue. Return true if the operation is successful. */
    public boolean enQueue(int value) {
        if(count == capacity) return false;
        // int tailIndex = (headIndex + count - 1) % capacity;
        queue[(headIndex + count) % capacity] = value;
        count++;
        return true;
    }
    
    /** Delete an element from the circular queue. Return true if the operation is successful. */
    public boolean deQueue() {
        if(count == 0) return false;
        headIndex = (headIndex + 1) % capacity;
        count--;
        return true;
    }
    
    /** Get the front item from the queue. */
    public int Front() {
        if(count == 0) return -1;
        return queue[headIndex];
    }
    
    /** Get the last item from the queue. */
    public int Rear() {
        if(count == 0) return -1;
        int tailIndex = (headIndex + count - 1) % capacity;
        return queue[tailIndex];
    }
    
    /** Checks whether the circular queue is empty or not. */
    public boolean isEmpty() {
        if(count == 0) return true;
        return false;
    }
    
    /** Checks whether the circular queue is full or not. */
    public boolean isFull() {
        if(count == capacity) return true;
        return false;
    }
}

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue obj = new MyCircularQueue(k);
 * boolean param_1 = obj.enQueue(value);
 * boolean param_2 = obj.deQueue();
 * int param_3 = obj.Front();
 * int param_4 = obj.Rear();
 * boolean param_5 = obj.isEmpty();
 * boolean param_6 = obj.isFull();
 */

复杂度分析

时间复杂度：O(1)
空间复杂度：O(n),n是队列容量capacity