LeetCode Notes_#279 完全平方数
Contents
题目
给定正整数n,找到若干个完全平方数(比如1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.思路分析
本题有点像剪绳子问题,要把一个数字拆分,且拆分出来的部分,要满足一个最优化的条件。
方法比较多,包括暴力递归,记忆化递归,动态规划,BFS,数学法。
比较常见的就是中间的3种,暴力递归性能差,数学法则没有普适性,需要记下来。记忆化递归和动态规划则思路非常相似。
所以记录了比较常见的,具有普适性的两种写法,动态规划法和BFS法。
解答
方法1:动态规划
- 计算平方数的数组,下标范围是
1~(int)sqrt(n),每个位置的元素是下标的平方 - 根据状态转移方程,从dp[0]开始计算,迭代地计算出dp[n],就是结果
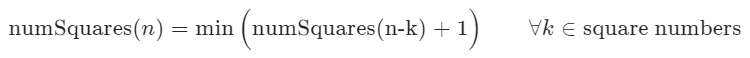
class Solution {
public int numSquares(int n) {
//[0,n]一共是n + 1个数字
int dp[] = new int[n + 1];
//因为下面用到Math.min取最小值,所以初始化为最大,否则可能不被更新
Arrays.fill(dp, Integer.MAX_VALUE);
//没有实际意义,因为输入都是正数
//设置为0可以正确计算dp[1],同时使得数组下标与numSquares(n)的结果对应起来
dp[0] = 0;
//max_square_index的数字的平方是小于n的最大数字,更大的平方数不可能组成n
int max_square_index = (int)Math.sqrt(n);
//存储所有可能组成n的平方数,下标范围是[1, max_square_index]
int[] square_nums = new int[max_square_index + 1];
for(int i = 1;i <= max_square_index;i++){
//square_nums[0]是默认值0
square_nums[i] = i * i;
}
//从dp[1]开始,迭代地计算出dp[n],就是最终结果
for(int i = 1;i <= n;i++){
for(int j = 1;j <= max_square_index;j++){
if(i >= square_nums[j])
dp[i] = Math.min(dp[i], dp[i - square_nums[j]] + 1);
}
}
return dp[n];
}
}
复杂度分析
时间复杂度: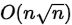
空间复杂度: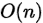
方法2:BFS
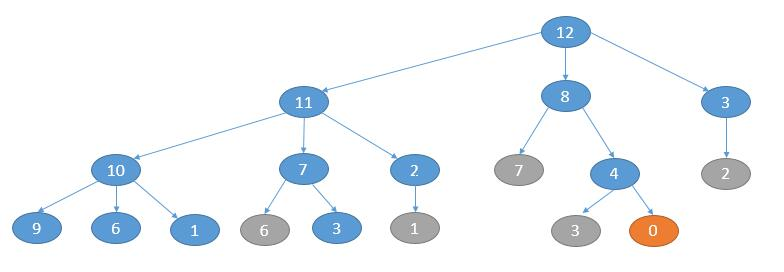
将原问题转化为一个n叉树的BFS遍历问题。
如下图,将输入的n作为根节点。
每个节点的孩子节点的值是当前节点减去一个平方数(依次减去1,4,9...)。
则值为0的节点距离根节点的最短路径就是结果。
例如下图中的橙色节点,距离根节点距离是3,可以写出分解的表达式12 = 4 + 4 + 4,每一条边代表的就是一个平方数。
代码和二叉树的层序遍历很相似,存在以下几个不同点:
- 这里的下一层节点不是通过左右指针来寻找,而是通过当前层节点减去平方数计算得到。
- 重复节点只需入队一次。
- 如果重复节点位于同一层,那么两个节点的子树结构完全相同,计算出来的最短路径一样,如果保留则造成多余的计算。
- 如果重复节点位于不同层,那么后访问到的节点必然离根节点更远,又因为两个节点的子树结构完全相同(即到0节点的距离相同),所以第二次之后访问的重复节点可以被忽略。
- 需要添加一个计数器
level,记录BFS的层数。
class Solution {
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<>();
//用于判断重复节点
HashSet<Integer> visited = new HashSet<>();
//level从0开始算起
int level = 0;
queue.offer(n);
visited.add(n);
while(!queue.isEmpty()){
//size是一层节点的数量
int size = queue.size();
for(int i = 0;i < size;i++){
int cur = queue.poll();
//遇到0节点,返回当前的level
if(cur == 0) return level;
for(int j = 1;j * j <= cur;j++){
int next = cur - j * j;//当前数字减去一个平方数,就是下一层的数字
if(!visited.contains(next)){
queue.offer(next);
visited.add(next);
}
}
}
level++;
}
//除非输入负数,不然任何数字都可以由1组成
return -1;
}
}官方题解中使用了HashSet数据结构,将其当作队列使用,还可以起到避免重复节点的作用。不过看知乎上的讨论,HashSet并不保证输出是有序的,是否有序跟jdk版本有关,所以最好别这样写。
Java遍历HashSet为什么输出是有序的? - 知乎
相比于官方题解,这个题解更加清晰,供参考。
详细通俗的思路分析,多解法
复杂度分析
不会分析...待学习
时间复杂度:O()
空间复杂度:O()

