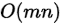LeetCode Notes_#221 最大正方形

LeetCode Notes_#221 最大正方形

Contents

• • 题目
  • 解答
    • 方法1：暴力
      • 复杂度分析
    • 方法2：动态规划
      • 复杂度分析

题目

解答

方法1：暴力

将要寻找的所有元素都是'1'的这种正方形称之为"1正方形"，那么每一个'1'位置肯定都是"1正方形"的左上角（即使'1'的周围全部是'0','1'本身就组成了一个边长为1的"1正方形"）。
我们要寻找的目标就是最大的"1正方形"的边长maxSide，由边长就可以计算出最大面积。这个边长的计算，可以看作一个逐步试探的过程，从任何一个'1'开始，朝着右下的对角线方向一格一格地延伸下去，每延伸一格就可以判断一次，当前区域的所有元素是否全部都是'1'，如果是，那么就可以得到一个更大的正方形，这时就更新最大边长maxSide。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return maxSide;
        int rows = matrix.length, columns = matrix[0].length;
        //两层循环遍历每个元素，对于所有1元素，获取以这个1作为左上角的最大正方形边长
        for(int i = 0; i < rows; i++){
            for(int j = 0; j < columns; j++){
                if(matrix[i][j] == '1'){
                    maxSide = Math.max(maxSide, 1);
                    //最大可能的边长
                    int currentMaxSide = Math.min(rows - i, columns - j);
                    //检验所有可能的边长的情况下，也就是[1...currentMaxSide]边长的正方形内，所有的格子内是否都是‘1’
                    //如果是，需要更新maxSide
                    for(int k = 1; k < currentMaxSide; k++){
                        boolean flag = true;
                        //新增的对角线上的元素如果是0，那么就不可能组成一个更大的正方形，跳出循环
                        if(matrix[i + k][j +k] == '0') break;
                        for(int m = 0; m < k; m++){
                            //matrix[i + k][j + m]表示新增的i+k行的所有元素
                            //matrix[i + m][j + k]表示新增的j+k列的所有元素
                            //这些元素必须都是1，如果是0，则直接跳出循环，且将flag置为false
                            if(matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0'){
                                flag = false;
                                break;
                            }
                        }
                        //循环结束，如果flag是true,表明没有遇到过0，所以说明从(i,j)到(i+k, j+k)坐标范围组成了1正方形,更新maxSide    
                        if(flag) maxSide = Math.max(maxSide, k + 1);
                        //否则，说明出现了0，那么（i,j）到（i+k,j+k）的坐标分为无法组成1正方形，所以就直接跳出循环
                        else break;
                    }
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}

复杂度分析

时间复杂度：
空间复杂度：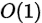
BTW,这个暴力法是可以通过的。

方法2：动态规划

动态规划三要素：

1. 状态： dp(i,j)表示以（i,j）为右下角，最大的“1正方形”的边长。
2. 状态转移方程： 分为如下两个情况：
   • （i,j）值为0：dp(i,j) = 0,因为(i,j)绝对不是“1正方形”的一部分
   • （i,j）值为1：dp(i,j) = min(dp(i - 1, j), dp(i, j - 1), dp(i - 1, j - 1)) + 1
     • 求最小值的一项，表示的是，(i,j)元素的左，上，左上元素的最大边长。取3者中最小的那个，原因是木桶理论，最小的那个边长决定了整体的边长，下图来自理解 三者取最小+1 - 最大正方形
       
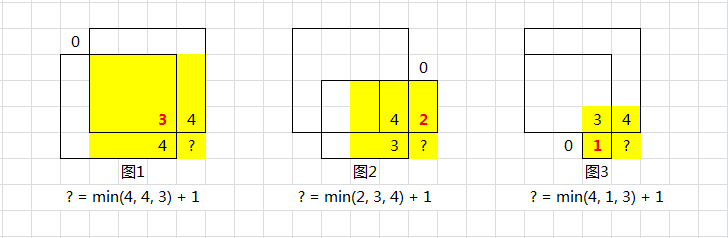
     • 最后的+1一项表示的是（i,j）元素以及他所在的行和列被加入到了之前的“1正方形”，所以边长+1

class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
        int maxSide = 0;
        int rows = matrix.length, cols = matrix[0].length;
        int[][] dp = new int[rows][cols];
        for(int i = 0; i < rows; i++){
            for(int j = 0; j < cols; j++){
                if(matrix[i][j] == '1'){
                    if(i == 0 || j == 0) dp[i][j] = 1;
                    else dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
                    maxSide = Math.max(maxSide, dp[i][j]);
                }
            }
        }
        System.out.println(maxSide);
        return maxSide * maxSide;
    }
}

复杂度分析

时间复杂度：
空间复杂度：