高数——三角函数 - 走看看

zoukankan html css js c++ java

高数——三角函数

链接：https://zhuanlan.zhihu.com/p/89073536

1 函数关系

1.1 倒数关系

$sinalpha·cscalpha=1$

$cosalpha·secalpha=1$

$analpha·cotalpha=1$

1.2 商数关系

$analpha=frac{sinalpha}{cosalpha}$

$cotalpha=frac{cosalpha}{sinalpha}$

1.3 平方关系

$sin^{2}alpha + cos^{2}alpha=1$ (1-3-1 式)

$1+ an^{2}alpha=sec^{2}alpha$

$1+cot^{2}alpha=csc^{2}alpha$

2 诱导公式

参考 $f(frac{k}{2}pipm alpha)=g(alpha),kin Z$ 奇变偶不变，符号看象限。
1）k为偶数，函数名不变。k为奇数，函数名余变正、正变余；
2）将 $alpha$ 视为锐角，观察原函数的函数值符号，将其赋给变换后的函数。

2.1 k为0，符号为负

$sin(-alpha) = -sin(alpha)$

$cos(-alpha) = cos(alpha)$

$an(-alpha) = - an(alpha)$

$cot(-alpha) = -cot(alpha)$

2.2 k为1，符号为负

$sin(frac{1}{2}pi-alpha) = cos(alpha)$

$cos(frac{1}{2}pi-alpha) = sin(alpha)$

$an(frac{1}{2}pi-alpha) = cot(alpha)$

$cot(frac{1}{2}pi-alpha) = an(alpha)$

2.3 k为2，符号为负

$sin(pi-alpha) = sin(alpha)$

$cos(pi-alpha) = -cos(alpha)$

$tan(pi-alpha) = -tan(alpha)$

$cot(pi-alpha) = -cot(alpha)$

2.4 k为2，符号为正

$sin(pi+alpha) = -sin(alpha)$

$cos(pi+alpha) = -cos(alpha)$

$an(pi+alpha) = an(alpha)$

$cot(pi+alpha) = cot(alpha)$

不再做更多举例。

3 二角和差公式

$sin(alpha + eta) = sinalpha · coseta + cosalpha · sineta$ (3-1 式)

$sin(alpha - eta) = sinalpha · coseta - cosalpha · sineta$ (3-2 式)

$cos(alpha + eta) = cosalpha · coseta - sinalpha · sineta$ (3-3 式)

$cos(alpha - eta) = cosalpha · coseta + sinalpha · sineta$ (3-4 式)

$an(alpha + eta)=frac{ analpha+ aneta}{1- analpha aneta}$ (3-5 式)

$an(alpha - eta)=frac{ analpha- aneta}{1+ analpha aneta}$ (3-6 式)

4 积化和差

4.1 公式列出

$cosalpha ·sineta=frac{1}{2}[sin(alpha + eta)-sin(alpha - eta)]$ (* 4-1 式)

$sinalpha ·coseta=frac{1}{2}[sin(alpha+ eta)+sin(alpha - eta)]$ (* 4-2 式)

$cosalpha · coseta = frac{1}{2}[cos(alpha - eta) + cos(alpha + eta)]$ (* 4-3 式)

$sinalpha · sineta = frac{1}{2}[cos(alpha - eta) - cos(alpha + eta)]$ (* 4-4 式)

4.2 记忆方法

4-1式 = 3-1式 - 3-2式

4-2式 = 3-1式 + 3-2式

4-3式 = 3-3式 + 3-4式

4-4式 = 3-3式 - 3-4式

5 和差化积

5.1 公式列出

$sinalpha + sineta=2sinfrac{alpha + eta}{2}cosfrac{alpha - eta}{2}$ (* 5-1 式)

$cosalpha + coseta=2cosfrac{alpha + eta}{2}cosfrac{alpha - eta}{2}$ (* 5-2 式)

$sinalpha - sineta=2cosfrac{alpha + eta}{2}sinfrac{alpha - eta}{2}$ (* 5-3 式)

$cosalpha - coseta=-2sinfrac{alpha + eta}{2}sinfrac{alpha - eta}{2}$ (* 5-4 式)

$analpha+ aneta=frac{sin(alpha + eta)}{cosalpha · coseta}$ (5-5 式)

5.2 记忆方法

5.2.1 口诀法

正加正，正在前，余加余，余并肩，正减正，余在前，余减余，负正弦。

5.2.2 推导法

观察 4-1式 4-2式 4-3式 4-4式，令 $u=alpha+eta$ , $v=alpha-eta$ ，有 $alpha=frac{u+v}{2}$ , $eta=frac{u-v}{2}$ 。用你 u, v 替换原式中 $alpha,eta$ 。

4-2式 ==( u, v 换元)==> 5-1式

4-3式 ==( u, v 换元)==> 5-2式

4-1式 ==( u, v 换元)==> 5-3式

4-4式 ==( u, v 换元)==> 5-4式

6 二倍角公式

6.1 公式列出

$sin2alpha=2sinalpha · cosalpha$ (* 6-1式)

$cos2alpha=cos^{2}alpha-sin^{2}alpha=2cos^{2}alpha-1=1-2sin^{2}alpha$ (* 6-2式)

$an2alpha=frac{2 analpha}{1- an^2alpha}$ (* 6-3式)

6.2 记忆方法

3-1式 ==( $eta$ 改为 $alpha$ )==> 6-1式

3-3式 ==( $eta$ 改为 $alpha$ )==(用 1-3-1式代还平方项)==> 6-2式

3-5式 ==( $eta$ 改为 $alpha$ )==> 6-3式

6.3 使用场景

6-2式常于化简时被用来降次升幂（或降幂升次）

7 半角公式（降幂公式）

7.1 公式列出

$sinfrac{alpha}{2}=pmsqrt{frac{1-cosalpha}{2}}$ (* 7-1式)

$cosfrac{alpha}{2}=pmsqrt{frac{1+cosalpha}{2}}$ (* 7-2式)

$anfrac{alpha}{2}= pmsqrt{frac{1-cosalpha}{1+cosalpha}}$ (* 7-3式)

$anfrac{alpha}{2}= frac{1-cosalpha}{sinalpha}$ (* 7-4式)

$anfrac{alpha}{2}= frac{sinalpha}{1+cosalpha}$ (* 7-5式)

7.2 记忆方法

注意到 6-2 式有 $2cos^2alpha-1$ 和 $1-2sin^2alpha$ 两种形式，通过整理后即可得到 7-1式、7-2式。

将 7-1式，7-2式相除，得到 7-3式。

7-4式和 7-5式待续。

8 万能公式

8.1 公式列出

$sinalpha=frac{2 anfrac{alpha}{2}}{1+ an^{2}frac{alpha}{2}}$ (* 8-1式)

$cosalpha=frac{1- an^{2}frac{alpha}{2}}{1+ an^{2}frac{alpha}{2}}$ (* 8-2式)

$analpha=frac{2 anfrac{alpha}{2}}{1- an^{2}frac{alpha}{2}}$ (* 8-3式)

8.2 记忆方法

8-1式和 8-2式待续。

8-3式和 6-3式是同一个公式。

9 正弦定理、余弦定理

9.1 正弦定理

$riangle ABC$ 的角 A, B, C 对应的 3 边分别为 a, b, c。其外接圆半径为R，则有

$frac{a}{sin A}=frac{b}{sin B}=frac{c}{sin C}=2R$

9.2 余弦定理

$riangle ABC$ 的角 A, B, C 对应的 3 边分别为 a, b, c。则有

$a^{2}=b^{2} + c^{2}-2bc·cos A$

$b^{2}=a^{2} + c^{2}-2ac·cos B$

$c^{2}=a^{2} + b^{2}-2ab·cos C$

10 常用反三角函数公式

10.1 $arcsinalpha+arccosalpha=frac{pi}{2}$

11 例题

11.1 求极限

1） $lim_{x ightarrow alpha}{frac{sin x-sinalpha}{x-alpha}}$ （高等数学第七版 1-9 习题 3.6）

2） $lim_{x ightarrow 0}{(1+3 an^{2}x)^{cot^{2}x}}$ （高等数学第七版 1-9 习题 4.4）

11.2 求导数

1） $y=frac{arcsin x}{arccos x}$ （高等数学第七版 2-2 习题 8.7）

2）计算摆线的参数方程

${_{y=a(1-cos t)}^{x=a(t-sin t),}$

所确定的函数 y=y(x)的二阶导数.（高等数学第七版 2-4 例9）

3）求 $y= an(x+y)$ 的二阶导数 $frac{d^2y}{dx^2}$ .（高等数学第七版 2-4 习题 3.3）

11.3 求根

1） $frac{cosxi}{1-sinxi}=frac{2}{pi-2}, xiin(0,frac{pi}{2})$ .(高等数学第七版 3-1 习题 3 倒数第二步)

11.4 求不定积分

1） $int_{}^{}sin^{3}xdx$ .(高等数学第七版 4-2 例题 11)

2） $int_{}^{}cos^{2}xdx$ .(高等数学第七版 4-2 例题 14)

3） $int_{}^{}csc xdx$ .(高等数学第七版 4-2 例题 18)

4） $int_{}^{}sec xdx$ .(高等数学第七版 4-2 例题 19)

5） $int_{}^{}cos3xcos2xdx$ .(高等数学第七版 4-2 例题 20)

6） $int_{}^{}frac{dx}{1+sqrt{1-x^2}}$ .(高等数学第七版 4-2 习题 2.41)

7） $int frac{sin x}{1+sin xcos x}dx$ .(知乎专栏数学杂谈用三角变换巧解一个不等式)

11.5

（本题1,2小问证明为定积分相关内容，想练习三角公式的同学直接使用1,2的结论求3即可）

设 $f(x)$ 是连续的周期函数，周期为T：

1）证明 $int_{a}^{a+T}fxdx=int_{0}^{T}f(x)dx$ ；

2）证明 $int_{a}^{a+nT}fxdx=nint_{0}^{T}f(x)dx（n in N）$ ；

3）计算 $int_{0}^{npi}sqrt{1+sin2x}dx$ .

(高等数学第七版 5-3 例7)

12 例题答案

11.1 求极限

1） $lim_{x ightarrow alpha}{frac{sin x-sinalpha}{x-alpha}}= lim_{x ightarrow alpha}{frac{cosfrac{x+alpha}{2}sinfrac{x-alpha}{2}}{frac{x-alpha}{2}}}= cosalpha$

2） $lim_{x ightarrow 0}{(1+3 an^{2}x)^{cot^{2}x}}= lim_{x ightarrow 0}{(1+3 an^3x)}^{frac{1}{3 an^3x}·3}= e^3$

11.2 求导数

1） $y^{'}= frac{frac{1}{sqrt{1-x^2}}·arccos x-arcsin x·(-frac{1}{sqrt{1-x^2}})}{arccos^{2}x}= frac{arcsin x+arccos x}{sqrt{1-x^2}arccos^2x}= frac{pi}{2sqrt{1-x^2}arccos^2x}$

2）

$frac{dy}{dx}= frac{frac{dy}{dt}}{frac{dx}{dt}}= frac{asin t}{a(1-cos t)}= frac{sin t}{1-cos t}= cotfrac{t}{2}spacespacespace(t e2npi,nin Z).$

$frac{d^2y}{dx^2}= frac{d}{dx}(frac{dy}{dx})= frac{d}{dt}(frac{dy}{dx})frac{1}{frac{dx}{dt}}= -frac{1}{2sin^2frac{t}{2}}·frac{1}{a(1-cos t)}= -frac{1}{a(1-cos t)^2}spacespacespace(t e2npi,nin Z)$

3）

$y'=[sec^2(x+y)]·(1+y')=[1+ an^2(x+y)]·(1+y')=(1+y^2)(1+y'),$

于是

$y'=frac{1+y^2}{1-(1+y^2)}=-frac{1}{y^2}-1$

$y''=frac{2y'}{y^3}=-frac{2(1+y^2)}{y^5}=-2csc^2(x+y)cot^3(x+y)$

11.3 求根

1） $frac{cosxi}{1-sinxi}=frac{2}{pi-2}$

$frac{frac{1- an^2frac{xi}{2}}{1+ an^2frac{xi}{2}}}{1-frac{2 anfrac{xi}{2}}{1+ an^2frac{xi}{2}}}= frac{2}{pi-2}$

$frac{1+ anfrac{xi}{2}}{1- anfrac{xi}{2}}=frac{2}{pi-2}$

$anfrac{xi}{2}=frac{4-pi}{pi}$

$xi=2arctan(frac{4-pi}{pi})$

11.4 求不定积分

1） $int_{}^{}sin^{3}xdx= int_{}^{}sin^{2}x·sin xdx= -int_{}^{}(1-cos^{2}x)·d(cos x)= -cos x+frac{1}{3}cos^{3}x+C$

2）

$int_{}^{}cos^{2}xdx= int_{}^{}frac{1+cos2x}{2}dx= int_{}^{}frac{1}{2}dx+int_{}^{}frac{cos2x}{4}d2x= frac{x}{2}+frac{sin2x}{4} + C$

3）

$int_{}^{}cscspace xdx= int_{}^{}frac{1}{sin x}dx= int_{}^{}frac{1}{2sinfrac{x}{2}·cosfrac{x}{2}}dx$

$= int_{}^{}frac{1}{ anfrac{x}{2}·cos^{2}frac{x}{2}}d(frac{x}{2})= int_{}^{}frac{1}{ anfrac{x}{2}}d( anfrac{x}{2})$

$=lnleft| anspace frac{x}{2} ight|+C$

或者因为

$anfrac{x}{2}= frac{sinfrac{x}{2}}{cosfrac{x}{2}}= frac{2sin^{2}frac{x}{2}}{sin x}= frac{1-cos x}{sin x}= csc x - cot x$

故不定积分也可表为

$int_{}^{}csc xdx= lnleft| csc x - cot x ight|+C$

$4） int_{}^{}sec xdx= int_{}^{}csc (x+frac{pi}{2})d(x+frac{pi}{2})$

应用上一题 11.4-3 结果

$= lnleft| csc(x+frac{pi}{2})-cot(x+frac{pi}{2}) ight|+C= lnleft| sec x + an x ight| + C$

5） $int_{}^{}cos3xcos2xdx$

$= int_{}^{}frac{1}{2}(cos5x + cos x)dx$

$= frac{1}{2}[int_{}^{}frac{1}{5}cos5xd5x + int_{}^{}cos xdx]$

$= frac{1}{10}sin5x + frac{1}{2}sin x + C$

6） $int_{}^{}frac{dx}{1+sqrt{1-x^2}}$

设 $x=sin t,space dx=cos tdt$

$int_{}^{}frac{dx}{1+sqrt{1-x^2}}= int_{}^{}frac{cos tdt}{1+cos t}$

$= int_{}^{}frac{(2cos^2frac{t}{2}-1)dt}{1+2cos^2frac{t}{2}-1}$

$= int dt-int sec^2frac{t}{2}dt$

$= t- anfrac{t}{2} + C$

$= t-frac{sin t}{1+cos t} + C$

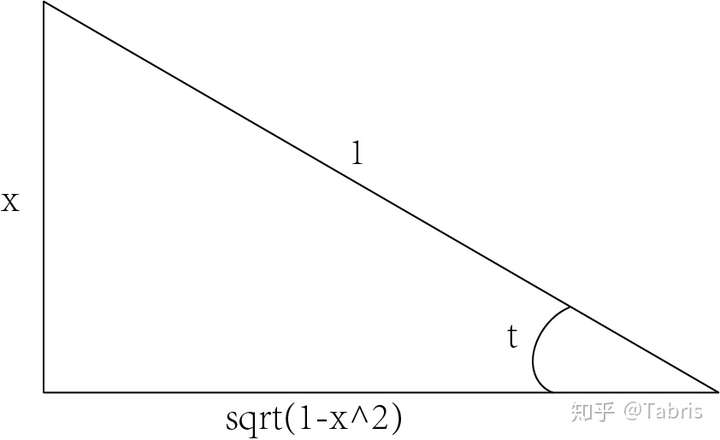t 角各边关系示意图

$= arcsin x-frac{x}{1+sqrt{1-x^2}} + C$

7） $int frac{sin x}{1+sin xcos x}dx$

$= frac{1}{2}int frac{sin x+cos x+sin x-cos x}{1+sin xcos x}dx$

$= frac{1}{2}[int frac{sin x+cos x}{1+sin xcos x}dx+int frac{sin x-cos x}{1+sin xcos x}dx]$

$= int frac{sin x+cos x}{3-(sin x-cos x)^2}dx+int frac{sin x-cos x}{1+(sin x+cos x)^2}dx$

$= int frac{d(sin x-cos x)}{3-(sin x-cos x)^2}-int frac{dx(sin x+cos x)}{1+(sin x+cos x)^2}$

$= frac{1}{2sqrt{3}}lnleft| frac{sin x - cos x + sqrt 3}{sin x - cos x - sqrt 3} ight|-arctan(sin x + cos x)+ C$

11.5

证：1）记 $phi(a)=int_{a}^{a+T}f(x)dx$ ，则

$phi'(a)=[int_{0}^{a+T}f(x)dx-int_{0}^{a}f(x)dx]'=f(a+T)-f(a)=0$ ，

知 $phi(a)$ 与 $a$ 无关，故 $phi(a)=phi(0)$ ，即

$int_{a}^{a+T}f(x)dx=int_{0}^{T}f(x)dx.$

2） $int_{a}^{a+nT}f(x)dx= sum_{k=0}^{n-1}{int_{a+kT}^{a+kT+T}f(x)dx}$ ，由1）知

$int_{a+kT}^{a+kT+T}f(x)dx= int_{0}^{T}f(x)dx$ ，

故

$int_{a}^{a+nT}f(x)dx= nint_{0}^{T}f(x)dx$

3） $int_{0}^{npi}sqrt{1+sin2x}dx$

$= nint_{0}^{pi}sqrt{1+sin2x}dx$

$= nint_{0}^{pi}left| sin x+cos x ight|dx$

$= sqrt 2nint_{0}^{pi}left| sin(x+frac{pi}{4}) ight|dx$

$= sqrt 2nint_{frac{pi}{4}}^{frac{5pi}{4}}left| sin(x) ight|dx$

$= sqrt 2nint_{0}^{pi}left| sin(x) ight|dx$

$= sqrt 2nint_{0}^{pi} sin(x)dx$

$= 2sqrt{2}n$

查看全文

相关阅读:
平衡二叉树
 二叉树的深度
 数字在升序数组中出现的次数
 美国最受雇主欢迎的十大编程语言
 重学数据结构（五、串）
重学数据结构（四、数组和广义表）
100个高频Spring面试题
 重学数据结构（三、队列）
重学数据结构（二、栈）
Java学习之jackson篇

原文地址：https://www.cnblogs.com/Hqx-curiosity/p/12252023.html

Copyright © 2011-2022 走看看