在《假设检验(Hypothesis Testing)》一文中,我们罗列了关于比较均值或方差的几种假设检验类型。除此之外,还有一种经常用到的检验类型,那就是比较比率(proportion)的假设检验。比如说,使用A方案的付费转化率为30%,使用B方案的付费转化率为34%,请问这两个转化率之间是否有显著不同?
总体比率是指总体中具体某种相同特征的个体所占的比值。通常用π表示总体比率,用p表示样本比率。比如某样本转化率为p的话,那么没有转化的人群比率就是1-p。这属于二项分布,当样本量足够大的时候,二项分布可以转换为正态分布。
比率类的假设检验有两种应用场景:比较样本比率和总体比率是否相同,比较两样本比率是否相同。
1,比较样本比率和总体比率是否相同,以此来检验样本和总体之间的差异(单样本比率检验):
当np≥5以及n(1-p)≥5时(大样本的情况下),p的抽样分布近似正态分布。因此,检验统计量可以选用z值: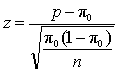 。
。
原假设: H0: π≥π0 H0: π≤π0 H0: π=π0 (样本和总体比率)
备择假设: Ha: π<π0 Ha: π>π0 Ha: π≠π0 (样本和总体比率)
(左尾) (右尾) (双尾)
拒绝法则(临界值法):如果z ≤ -zα,则拒绝原假设(左尾)
如果z ≥ zα,则拒绝原假设(右尾)
如果z ≤ -zα/2 或 z ≥ zα/2,则拒绝原假设(双尾)
拒绝法则(p值法):如果p值≤α,则拒绝原假设
2,比较两样本比率是否相同,以此来检验两总体之间的差异(两独立样本比率检验):
当np1≥5,np2≥5以及n(1-p1)≥5,n(1-p2)≥5时(大样本的情况下),p1-p2差值的抽样分布近似正态分布。因此,检验统计量可以选用z值: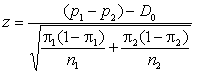 。
。
由于π1和π2未知(这不是废话嘛,要是已知的话直接就能知道这两个总体比率是否相同了),那么就需要用样本比率来对总体比率进行估计,这里分为两种情况:
一种情况是原假设π1-π2=D0(D0=0)为真,也就是两总体比率相同,那么就可以统一用p( )来估计总体比率,检验统计量就可以写成:
)来估计总体比率,检验统计量就可以写成: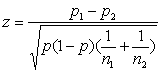 。
。
另一种情况是原假设π1-π2=D0(D0≠0)为真,也就是两总体比率不同,分别用p1和p2来估计两总体的比率,检验统计量就可以写成: 。
。
原假设: H0: π1≥π2 H0: π1≤π2 H0: π1=π2 (样本和总体比率)
备择假设: Ha: π1<π2 Ha: π1>π2 Ha: π1≠π2 (样本和总体比率)
(左尾) (右尾) (双尾)
拒绝法则(临界值法):如果z ≤ -zα,则拒绝原假设(左尾)
如果z ≥ zα,则拒绝原假设(右尾)
如果z ≤ -zα/2 或 z ≥ zα/2,则拒绝原假设(双尾)
拒绝法则(p值法):如果p值≤α,则拒绝原假设
可以用G*Power或statsmodels进行比率假设检验:
statsmodels:statsmodels.stats.proportion.proportions_ztest(count, nobs, value=None, alternative='two-sided', prop_var=False)
返回:z统计量的具体值和p值。
计算效应量:
公式:2 * (arcsin(sqrt(p1)) - arcsin(sqrt(p2))) (cohen's h)
statsmodels:statsmodels.stats.proportion.proportion_effectsize(prop1, prop2, method='normal') (两总体比率)
计算样本量&功效:
statsmodels:statsmodels.stats.power.zt_ind_solve_power(effect_size=None, nobs1=None, alpha=None, power=None, ratio=1.0, alternative='two-sided')
附:
比率类的假设检验,其最小样本量的计算公式为:(摘自:https://jeffshow.com/caculate-abtest-required-sample-size.html)
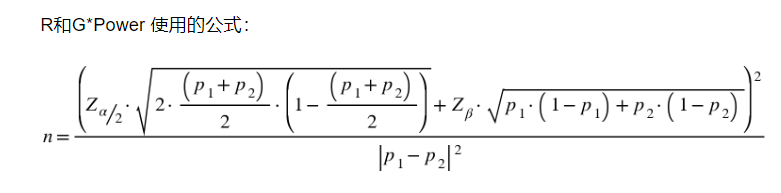
p1我们称为基础值,是实验关注的关键指标现在的数值(对照组);p2我们称为目标值,是希望通过实验将其改善至的水平;通常设定α为0.05,β为0.2