题目描述
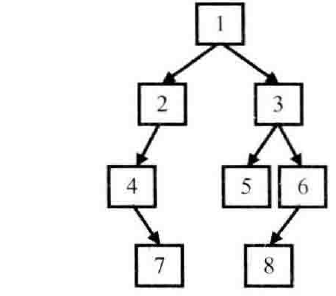
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
考点
考察对二叉树遍历方式的理解,以及如何把构建二叉树的大问题分解为构建左、右子树的两个小问题(递归)。
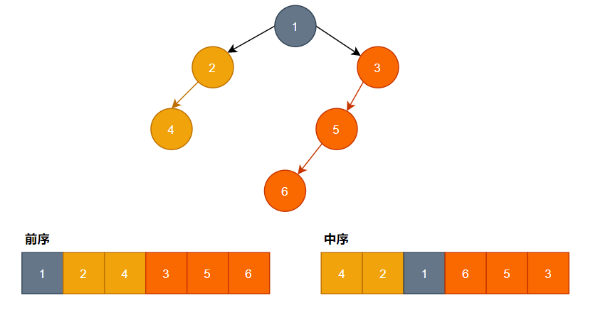
- 二叉树的前序遍历:根左右
- 二叉树的中序遍历:左根右
- 二叉树的的后序遍历:左右根
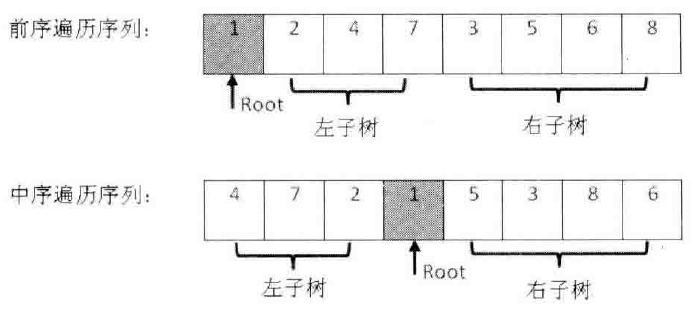
在二叉树的前序遍历序列中,第一个数字总是树的根节点的值。
在中序遍历序列中,根节点的值在序列的中间,左子树的节点的值位于根节点的值的左边,右子树的节点的值位于根节点的值的右边。
思路
根据中序遍历和前序遍历可以确定二叉树,具体过程为:
- 根据前序序列第一个结点确定根结点
- 根据根结点在中序序列中的位置分割出左右两个子序列
- 对左子树和右子树分别递归使用同样的方法继续分解
☆☆代码实现
/** * Definition for binary tree * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Solution { public TreeNode reConstructBinaryTree(int [] pre,int [] in) { TreeNode root = ConstructCore(pre,0,pre.length-1,in,0,in.length-1); return root; } public TreeNode ConstructCore(int[] pre,int startPre,int endPre,int [] in,int startIn,int endIn){ if (startPre > endPre || startIn > endIn) return null; TreeNode root = new TreeNode(pre[startPre]); for(int i = startIn; i <= endIn; i++){ if(in[i] == pre[startPre]){ root.left = ConstructCore(pre,startPre+1,startPre+i-startIn,in,startIn,i-1); root.right = ConstructCore(pre,startPre+i-startIn+1,endPre,in,i+1,endIn); break; } } return root; } }
参考: