注释:
转载请注明出处http://www.cnblogs.com/HuisClos/articles/6966036.html
在我们所讨论的三度空间(三维)中,能够出现的微分形式只有四种:
零次微分形式——函数 f
一次微分形式——线积分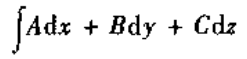 中出现的微分dx,dy,dz的一次式
中出现的微分dx,dy,dz的一次式
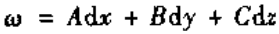
二次微分形式——面积分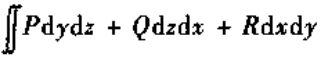 中出现的微分dx,dy,dz的二次式
中出现的微分dx,dy,dz的二次式
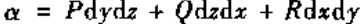
三次微分形式——体积分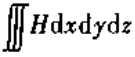 中出现的微分dx,dy,dz的三次式
中出现的微分dx,dy,dz的三次式

注意:以上微分形式中至少有两个相同的dx,dy,dz项,每一个形式中只包含具有不同的dx,dy,dz的项。
我们还知道联系这些线、面、体积分的三个基本公式:
Green公式:
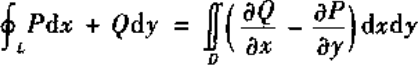
其中D为L围成的闭区域,P、Q为D上的具有一阶连续偏微商的函数。
Gauss公式:

其中V为封闭曲面∑围成的闭区域,函数P、Q、R为V上有一阶连续偏微商的函数。
Stokes公式:
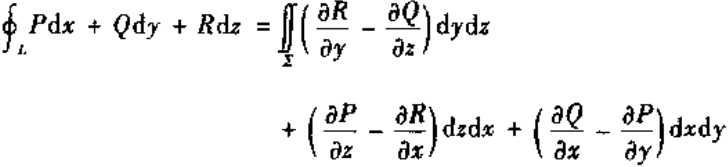
其中封闭曲线L为曲面∑的边界,P、Q、R为V上有一阶连续偏微商的函数。
那么上述三个公式之间有什么联系?
这就是本文所要关注的。
我们也很容易联想到上述三个公式的更一般形式的物理意义,即场论中的三个度——梯度、旋度、散度
设 u 为数量场,v = Pi + Qj + Rk 为矢量场。
梯度:
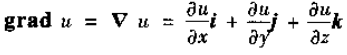
旋度:
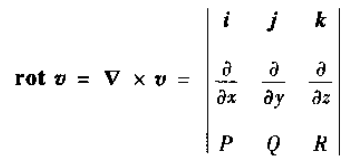
散度:

这些度都是怎样产生的?有何数学意义?
这也是本文所要关注的。
单变量微积分有Newton-Leibniz公式,即微分与积分是一对对立统一的运算
多变量微积分中微分、积分的对立统一是怎样体现的?
这又是本文所要关注的。
怀着这三种疑惑,我们开始观察这些积分。
容易发现,
第二型线、面积分的积分区域都是有方向的。
然后容易想到可以把一重积分、二重积分看作第二型线、面积分的特例:积分区域也有方向。
三重积分同理也可定向。
所以,曲线长度因方向不同被定义成正负,亦如单变量微积分中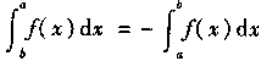 的这个性质。
的这个性质。
关于曲面,
定向是分为内外侧(看课本定义,即法线从起点连续移动直到回到起点,根据法线方向是否改变来为曲面定向)
(不可定向的曲面典型就是著名的莫比乌斯带。)
来张图吧
 莫比乌斯带——不可定向
莫比乌斯带——不可定向
那么我们在这里只能讨论可定向的曲面咯。
所以,曲面面积在面积元素定向后因方向不同被被定义成正负。
根据二重积分定义,再将面积元素进行变元变换(看课本定义,不详细写)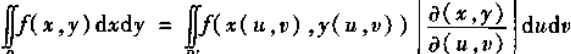
当时是为了保持面积元素始终为正,而对式中Jacobi行列式取了绝对值。
但是现在,面积元素被允许有正负了,就没必要取绝对值了,就变成了这样
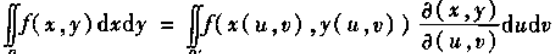
其中D已定向,D’是D经过变元逆变换得到的区域,自然是定向了的。
所以,
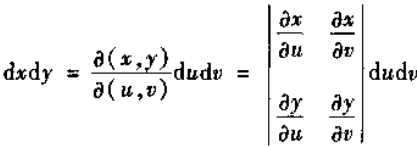
观察此式的性质
(i)如果取y = x,则有
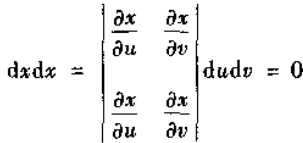
(ii)如果将y,x互换,则有


此时,dydx≠dxdy,即dx,dy在乘积中次序不能颠倒,否则就是正负的差别。
满足上述两条的微分乘积被称为微分的外乘积,记为 
即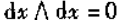 和
和 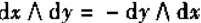 第二条和普通的微分乘积不同。
第二条和普通的微分乘积不同。
外微分形式:
由微分的外乘积乘函数组成的微分形式:
若P、Q、R、A、B、C、H为x,y,z的函数,
一次外微分形式: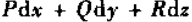
二次外微分形式:
三次外微分形式: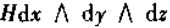
接下来易证得三个外微分形式λ,µ,ν的外乘积满足分配律、结合律,但不满足交换律。(证明比较简单但编辑起来略繁就不贴了):
如果λ,µ,ν是任意三个外微分形式
分配律:


交换律:
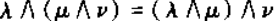
不满足结合律:
若µ为p次外微分形式,λ为q次外微分形式
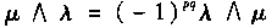
这些定律用于后期推广证明。
容易联想到
外微分可类比为:矢量外乘积
为了便于推广,我们可根据形式定义算子。
因此我们根据外微分形式ω定义外微分算子d,
零次外微分形式 函数 f 定义为
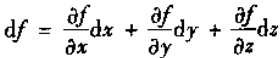 ,其实这里就是普通的全微分算子
,其实这里就是普通的全微分算子
一次外微分形式 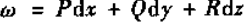 ,定义为
,定义为

由于
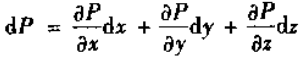


所以


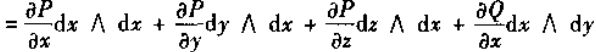
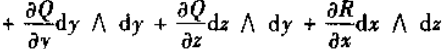
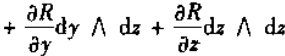
由于
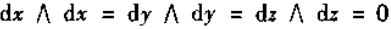



所以
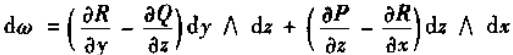
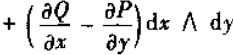
二次外微分形式 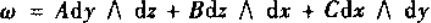 ,定义为
,定义为

同理易得

三次外微分形式 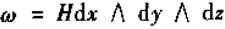 ,定义为
,定义为
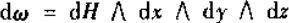
同理,由于

所以
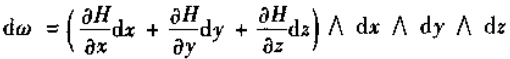


为什么等于零?因为每一项中至少有两个微分是相同的
所以,在三维空间中任意的三次外微分形式的外微分是零
外微分算子和普通微分算子运算方式相同,唯一的不同就是外微分算子运算后进行外乘积,而普通微分算子运算后进行正常的乘积。
于是我们得到了零次、一次、二次、三次外微分算子。
接下来,
设零次外微分形式ω=f,
就有
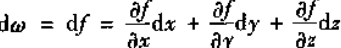
然后
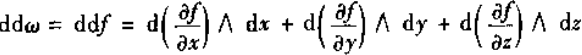
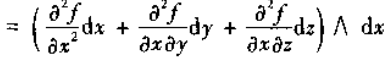
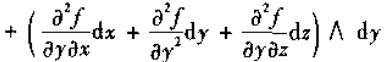

由于
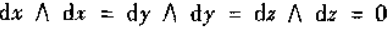


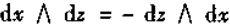
所以
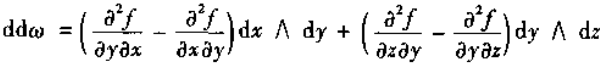

假设f具有二阶连续偏微商,则有
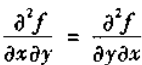
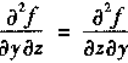
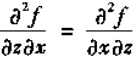
所以

一次外微分形式 

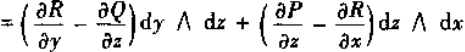

于是
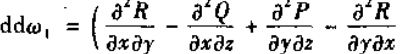

二次外微分形式

易得
三次外微分形式
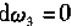
易得 
这就是Poincaré引理:
若ω为一个外微分形式,其微分形式的系数具有二阶连续偏微商,则 。
。
那么Poincaré引理的逆定理是否成立呢?成立。
先阐述Poincaré引理之逆:
若ω是一个p次外微分式且 ,则存在一个p-1次外微分形式 a,使
,则存在一个p-1次外微分形式 a,使 。
。
其实我们学习场论中的有势场、管型场时已经证明过了。
这里具体不贴了。
引入外微分后,接下来回到之前的疑惑之一——场论中的三个度究竟是什么含义,还有没更多的度?
先将三个度化成外微分形式,观察其意义。
零次外微分形式 ω = f, 零次外微分形式的外微分
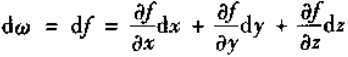
又 f 的梯度为

所以梯度与零次外微分形式的外微分相对应。
一次外微分形式 的外微分
的外微分



又矢量  的旋度为
的旋度为
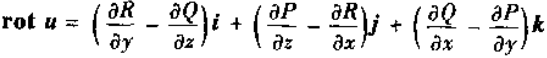
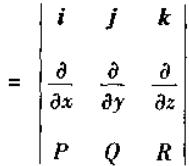
所以旋度与一次外微分形式的外微分相对应。
二次外微分形式 的外微分
的外微分

又矢量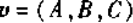 的散度
的散度

所以散度与二次外微分形式的外微分相对应。
三次外微分形式的外微分在三维空间中为零。
所以没有相对应的度。
三维空间里,也没有更多的度了。
综上,就是如下
外微分形式的次数 度
0 梯度
1 旋度
2 散度
那么,Poincaré引理与Poincaré引理之逆也有其场论意义了:
易得
Poincaré引理中
当ω为零次外微分形式ω = f,有
即 
当ω为一次外微分形式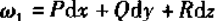 ,记
,记 ,有
,有 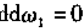
即 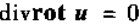
Poincaré引理之逆中
 等价于
等价于
即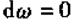 必有
必有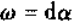
 等价于
等价于

即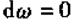 必有
必有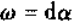
回到剩下两个疑惑——三个公式与高维空间中微分积分的关系
现将三个公式写成外微分形式。
Green公式

记 ,为一次外微分形式,于是
,为一次外微分形式,于是
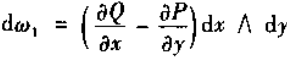
又线积分L可定向,所以该公式可写成

同理,Gauss公式


又Σ定向,所以记
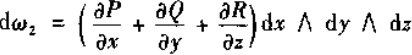
该公式可写成

同理Stokes公式
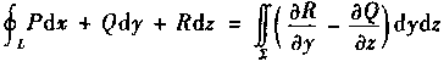
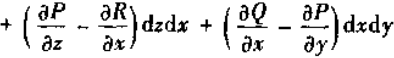
又线、面积分都为定向,将 看作一次外微分形式
看作一次外微分形式


所以该公式可写成

综上,可以看出,Green公式、Gauss公式、Stokes公式实际上是一个公式

其中ω为外微分形式,dω为ω的外微分,Σ为dω的封闭积分区域,∂Σ为Σ的边界,∫为区域有多少维数即多少重数。
含义:
高次的外微分形式dω在区域上的积分等于低一次的外微分形式ω在区域的低一维空间边界上的积分。
外微分运算和积分是相互抵消的,亦如一维空间中Newton-Leibniz公式。
由于三维空间中三次外微分形式的外微分为零,所以有了这个公式以后,区分区域和边界的公式就不再有了。
这个公式就是广义的Stokes公式
再写一遍

这个公式还可以推广到更一般的流形上(这个未来再说)
综上,在三维空间中,
外微分形式的次数 空间 公式
0 直线段 Newton-Leibniz公式
1 平面区域 Green公式
1 空间曲面 Stokes公式
2 空间中区域 Gauss公式
完