链表应用：一元多项式运算器。

链表应用：一元多项式运算器。

基本要求：

（1）输入并建立多项式，并用友好的界面显示多项式，如，8x³-6x²+8显示为8x^3-6x^2+8；

（2）计算两个多项式的加法和减法；

（3）给定x，计算多项式在x处的值

代码如下

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>

typedef struct Polynode{
    int coef;
    int exp;
    Polynode *next;
}Polynode, *Polylist;

void Initlist(Polylist *L);
Polylist Createlist(Polylist L);
void Showlist(Polylist L);
void PolyAdd(Polylist polya, Polylist polyb, Polylist polyc);
void PolySub(Polylist polya, Polylist polyb, Polylist polyc);
int evaluationAtX(Polylist L, int x);

void Initlist(Polylist *L){
    *L = (Polylist)malloc(sizeof(Polylist));
    (*L)->next = NULL;
}

/*创建存储多项式的链表，输入书系数有小变大*/ 
Polylist Createlist(Polylist L){
    Polynode *pre, *rear;
    pre = rear = L;
    rear = (Polynode *)malloc(sizeof(Polynode));
    scanf("%d %d", &rear->coef, &rear->exp);
    while(rear->coef){
        pre->next = rear;
        pre = rear;
        rear = (Polynode*)malloc(sizeof(Polynode));
        scanf("%d %d", &rear->coef, &rear->exp);
    }
    free(rear);
    pre->next = NULL;
    return L;
}

//输出多项式，注意格式，还有显示的细节 
void Showlist(Polylist L){ 
    Polynode *p = L->next;
    if(p->exp == 0){
        printf("%d", p->coef);
    }
    else{
        printf("%dx^%d", p->coef, p->exp);
    }
    
    for(p = p->next; p != NULL; p = p->next){
        if(p->exp == 0 ){
            if(p->coef < 0)
            printf("%d", p->coef);
            else
            printf("+%d", p->coef);
        }
        else{
            if(p->coef < 0){
                if(p->coef == -1 && p->exp == 1){
                    printf("-x");
                }
                else if(p->coef != -1 && p->exp == 1){
                    printf("%dx", p->coef);
                }
                else if(p->coef == -1 && p->exp != 1){
                    printf("-x^%d", p->exp);
                }
                else{
                    printf("%dx^%d", p->coef, p->exp);
                }
            }
            else{
                if(p->coef == 1 && p->exp == 1){
                    printf("+x");
                }
                else if(p->coef != 1 && p->exp == 1){
                    printf("+%dx", p->coef);
                }
                else if(p->coef == 1 && p->exp != 1){
                    printf("+x^%d", p->exp);
                }
                else{
                    printf("+%dx^%d", p->coef, p->exp);
                }
            }
        }
    }
    printf("
");
}

/*polyc链表用来保存加和得到的结果，不能利用现有链表节点，也不能销毁链表节点 ,不然操作只是一次性的
以下函数实现polyc = polya + polyb*/ 
void PolyAdd(Polylist polya, Polylist polyb, Polylist polyc){
    Polynode *p, *q, *pre, *rear;
    int sum;
    p = polya->next;
    q = polyb->next;
    pre = rear = polyc;
    while(p != NULL && q != NULL){//系数之间大小只有三种情况，分类处理 
        if(p->exp < q->exp){
            rear = (Polynode*)malloc(sizeof(Polynode));
            rear->coef = p->coef;
            rear->exp = p->exp;
            pre->next = rear;
            pre = rear;
            p = p->next;
        }
        else if(p->exp == q->exp){//只有系数相等时才进行运算 
            sum = p->coef + q->coef;
            if(sum != 0){
                rear = (Polynode*)malloc(sizeof(Polynode));
                rear->coef = sum;
                rear->exp = p->exp;
                pre->next = rear;
                pre = rear;
                p = p->next;
                q = q->next;
            }
            else{
                p = p->next;
                q = q->next;
            }
        }
        else{
            rear = (Polynode*)malloc(sizeof(Polynode));
            rear->coef = q->coef;
            rear->exp = q->exp;
            pre->next = rear;
            pre = rear;
            q = q->next;
        }
    }
    //把没有处理完的多项式进行处理 
    if(p != NULL){
        while(p != NULL){
            rear = (Polynode*)malloc(sizeof(Polynode));
            rear->coef = p->coef;
            rear->exp = p->exp;
            pre->next = rear;
            pre = rear;
            p = p->next; 
        }
    }
    if(q != NULL){
        while(q != NULL){
            rear = (Polynode*)malloc(sizeof(Polynode));
            rear->coef = q->coef;
            rear->exp = q->exp;
            pre->next = rear;
            pre = rear;
            q = q->next;
        }
    }
    rear->next = NULL;
}

/*其实也可以在加法的代码上稍加改动便可以实现减法，但是感觉这样会使代码比较长，所以我选择用： 
多项式减法其实就是多项式加法，实现polya - polyb*/
void PolySub(Polylist polya, Polylist polyb, Polylist polyc){
    Polylist t;
    Initlist(&t);
    Polynode *pre, *rear;
    pre = rear = t; 
    //找一个中间链表t，来存储 -polyb
    for(Polynode *p = polyb->next; p != NULL; p = p->next){ 
        rear = (Polynode*)malloc(sizeof(Polynode));
        rear->coef = -1 * p->coef;
        rear->exp = p->exp;
        pre->next = rear;
        pre = rear;
    }
    pre->next = NULL;
    PolyAdd(polya, t, polyc);
    pre = t;
    while(pre != NULL){//释放掉 t
        rear = pre->next;
        free(pre);
        pre = rear;
    }
}

//计算多项式在x = x时的值 
int evaluationAtX(Polylist L, int x){
    int sum = 0;
    for(Polynode *p = L->next; p != NULL; p = p->next){
        sum += p->coef * pow(x, p->exp);
    }
    return sum;
}

int main(){
    Polylist La, Lb, Lc, Ld;
    Initlist(&La);
    Initlist(&Lb);
    Initlist(&Lc);
    Initlist(&Ld);
    La = Createlist(La);
    printf("La = ");
    Showlist(La);
    Lb = Createlist(Lb);
    printf("Lb = ");
    Showlist(Lb);
    PolyAdd(La, Lb, Lc);
    printf("Lc = ");
    Showlist(Lc);
    PolySub(La, Lb, Ld);
    printf("Ld = ");
    Showlist(Ld);
    int x = 2;
    printf("lc(%d) = %d
", x, evaluationAtX(Lc, x));
    return 0;
}

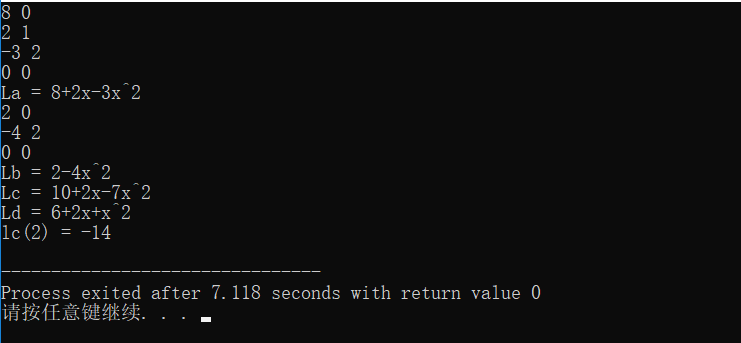
运行结果如下：