题目信息
-
时间: 2019-07-06
-
题目链接:Leetcode
-
tag: 动态规划 迭代 约瑟夫环
-
难易程度:中等
-
题目描述:
0,1,,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例1:
输入: n = 5, m = 3
输出: 3
示例2:
输入: n = 10, m = 17
输出: 2
注意
1. 1 <= n <= 10^5
2. 1 <= m <= 10^6
解题思路
本题难点
约瑟夫环
N个人围成一圈,第一个人从1开始报数,报M的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,求最后的胜利者。
具体思路
约塞夫问题就是用人来举例的,那我们也给每个人一个编号(索引值),每个人用字母代替
下面这个例子是N=8 m=3的例子
我们定义F(n,m)表示最后剩下那个人的索引号,因此我们只关系最后剩下来这个人的索引号的变化情况即可
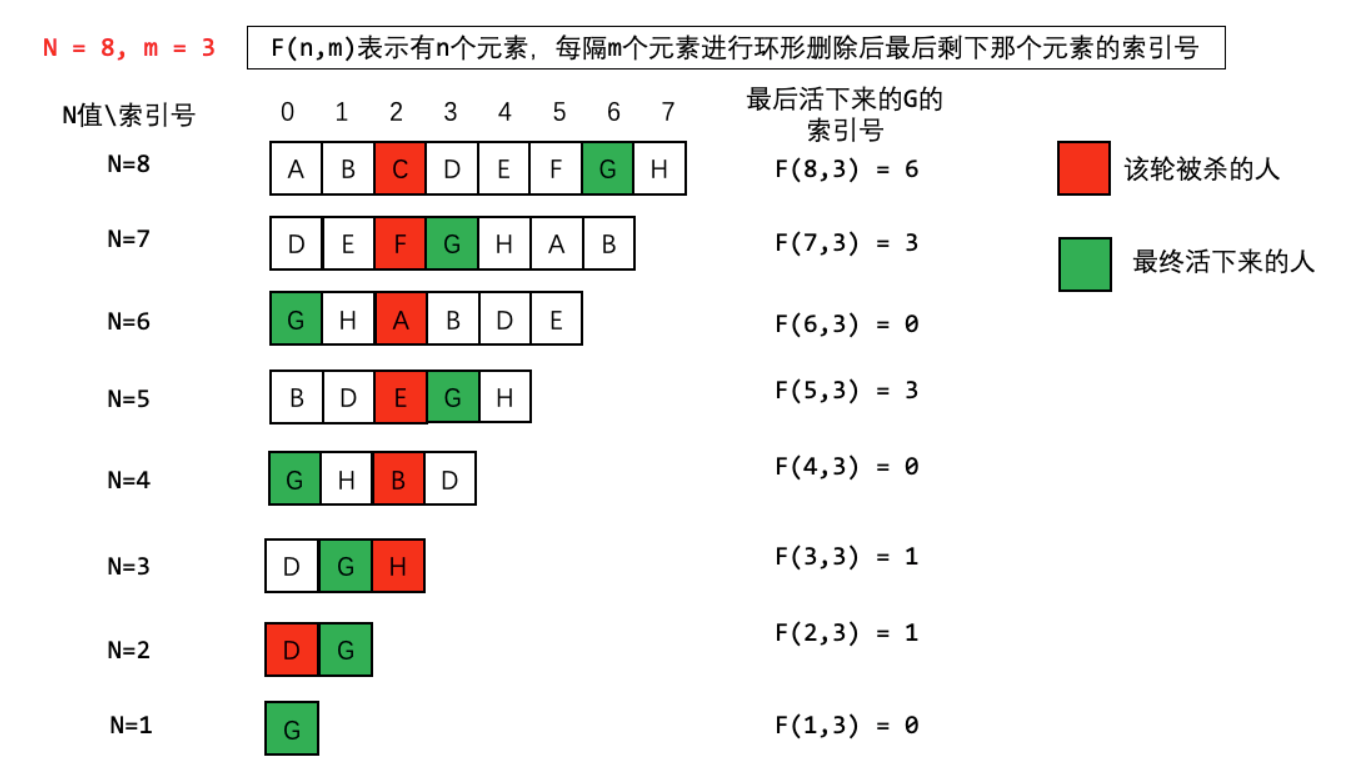
从8个人开始,每次杀掉一个人,去掉被杀的人,然后把杀掉那个人之后的第一个人作为开头重新编号
- 第一次C被杀掉,人数变成7,D作为开头,(最终活下来的G的编号从6变成3)
- 第二次F被杀掉,人数变成6,G作为开头,(最终活下来的G的编号从3变成0)
- 第三次A被杀掉,人数变成5,B作为开头,(最终活下来的G的编号从0变成3)
- 以此类推,当只剩一个人时,他的编号必定为0!(重点!)
现在我们知道了G的索引号的变化过程,那么我们反推一下
从N = 7 到N = 8 的过程
如何才能将N = 7 的排列变回到N = 8 呢?
我们先把被杀掉的C补充回来,然后右移m个人,发现溢出了,再把溢出的补充在最前面
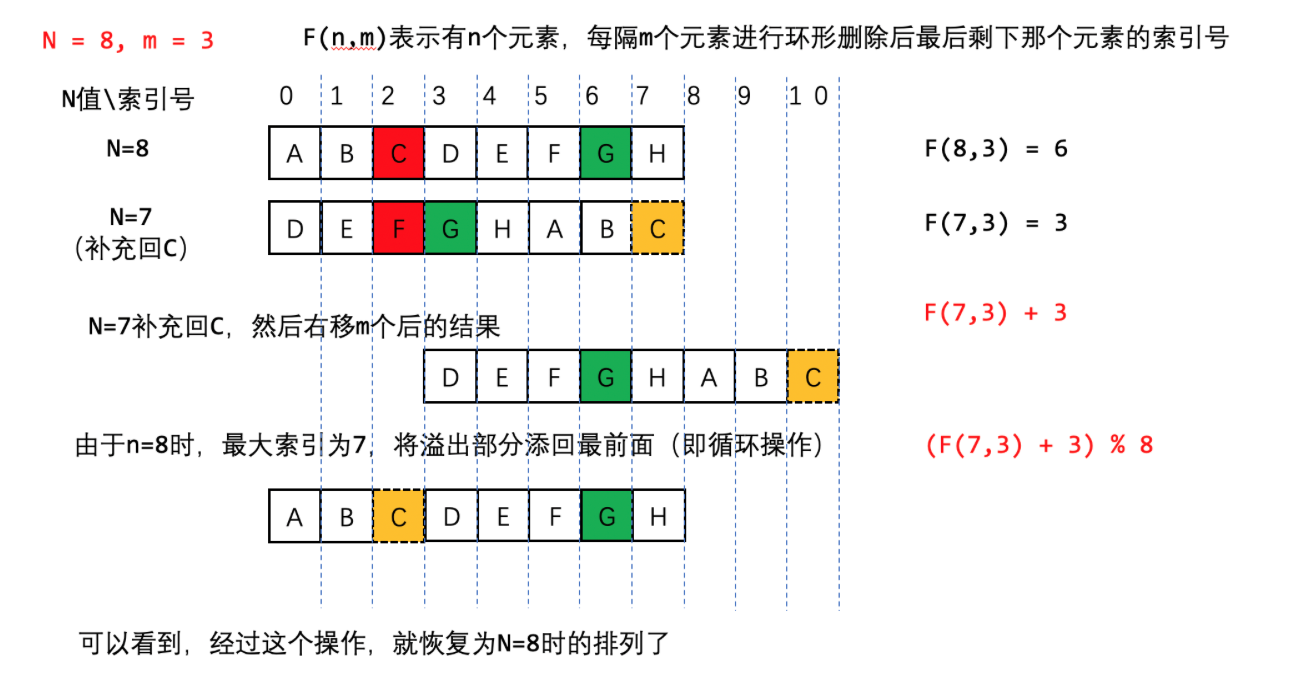
因此我们可以推出递推公式f(8,3)=[f(7,3)+3]%8
进行推广泛化,即f(n,m)=[f(n−1,m)+m]%n
- 递推公式
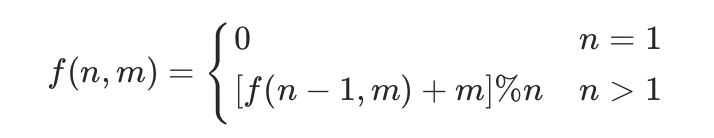
提示 : 最终剩下的数字的数组下标为0;
代码
class Solution {
public int lastRemaining(int n, int m) {
int res = 0 ;
for(int i = 2 ; i <= n; i++){
res = (res + m) % i;
}
return res;
}
}
复杂度分析:
- 时间复杂度 O(N) :其中 N为 迭代n次的长度。
- 空间复杂度 O(1) : 变量 res 使用常数大小的额外空间。
其他优秀解答
解题思路
模拟链表。纯暴力的做法,每次找到删除的那个数字,需要 O(m) 的时间复杂度,然后删除了 n−1 次。但实际上我们可以直接找到下一个要删除的位置的。假设当前删除的位置是 idx,下一个删除的数字的位置是 idx+m 。但是,由于把当前位置的数字删除了,后面的数字会前移一位,所以实际的下一个位置是 idx+m−1。由于数到末尾会从头继续数,所以最后取模一下,就是 (idx+m−1)(modn)。
代码
class Solution {
public int lastRemaining(int n, int m) {
ArrayList<Integer> list = new ArrayList<>(n);
for (int i = 0; i < n; i++) {
list.add(i);
}
int idx = 0;
while (n > 1) {
idx = (idx + m - 1) % n;
list.remove(idx);
n--;
}
return list.get(0);
}
}