第 1 章 排序
桶排序
冒泡排序
快速排序
第 2 章 栈、队列、链表
队列
栈
链表
模拟链表
第 3 章 枚举!很暴力
奥数
数的全排列
第 4 章 万能的搜索
深度优先搜索
广度优先搜索
第 5 章 图的遍历
深度和广度优先
图的深度优先遍历
图的广度优先遍历
第 6 章 最短路径
第 1节 只有五行的算法——Floyd-Warshall
第 2节 Dijkstra算法——通过边实现松弛
第 3节 Bellman-Ford——解决负权边
第 4节 Bellman-Ford的队列优化
第 5节 最短路径算法对比分析
第 7 章 神奇的树
二叉树
堆
并查集
》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》
1.1桶排序---O(N+M)
1.2冒泡排序---O(N^2)
核心:双重嵌套循环
1.3快速排序(二分法)---O(NlogN)
1)找基准数
2)先从右往左找到一个小于6的数,再从左往右找一个大于6的数,交换
1.4 去重、排序
第一种方法:桶排序、
第二种方法:先排序、后去重,冒泡排序或者快速排序
2.1 队列
线性结构,只允许在队列的首部 head 进行删除,在队列的尾部 tail 插入
例子:买票;先进先出 FIFO
结构体类型:
struct queue { int data[100];//队列的主体,用来存储内容 int head;//队首 int tail;//队尾 };
2.2 栈
例子:小桶放球;后进先出
top:指向栈顶的变量
用途:判断回文词,
2.4 链表
C语言中,可以使用 指针和函数malloc来实现。
也可以用数组模拟链表
结构体 node,两个成员,data和指针
struct node *head; head = NULL;//头指针为空 struct node *p; //动态申请一个空间,用来存放一个结点,并用临时指针p指向这个结点 p = (struct node *)malloc(sizeof(struct node)); scanf("%d",&a); p->data = a;//将数据存储到当前结点的data域中 p->next = NULL;//设置当前结点的后继指针指向空,也就是当前结点的下一个结点为空
->叫做结构体指针运算符,也是用来访问结构体内部成员的。因为此处p是一个指针,所以不能使用.号访问内部成员。
2.5 模拟链表
用数组模拟链表
两个数组,data 和 left
3.1 枚举
3.2 炸弹人
使用数组模拟地图
3.3 火柴棍模式
核心是 求方程的解,
3.4 数的全排列
4.1 深度优先搜索 (Depth First Search, DFS)
基本模型
void dfs(int step) { //判断边界 //尝试每一种可能 for(i=1;i<=n;i++) { 继续下一步 dfs(step+1); } 返回 }
数字全排列
4.2 迷宫问题
4.3 广度优先搜索(宽度优先搜索)Breadth First Search, BFS
层层递增
4.4 炸弹人 用 dps、bfs 解
4.5 宝岛探险
4.5 水管工游戏
五、图的遍历
5.1 深度和广度优先
图的邻接矩阵法
5.2 图的深度优先遍历
六、最短路径
6.1 Floyd-Warshall,
6.2 Dijikstra 算法——通过边实现松弛
曲线救国
6.3 Bellman-Fod——解决负权边
for(k=1;k<=n-1;k++) for(i=1;i<=m;i++) if(dis[v[i]] > dis[u[i]] + w[i]) dis[v[i]] = dis[u[i]] + w[i];
6.4 Bellman-Ford 的队列优化
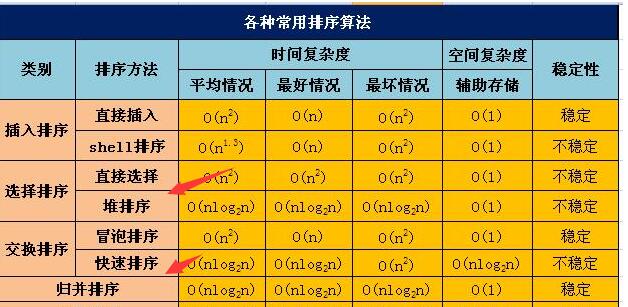
6.5 最短路径算法对比分析
七、树
7.1 树
树:不包含回路
图:包含回路
树的特点:1,树中的任意两个结点有且只有一条路径联通。2,n个结点则有n条边。3,在一棵树中加一条边将会构成一个回路。
7.2 二叉树
完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
满二叉树的任意节点,要么度为0,要么度为2.
7.3 堆
一种特殊的二叉树
最小堆:所有父节点都比子节点要小
最大堆:所有父节点都比子节点要大
应用:
优先队列:支持插入元素和寻找最大(小)值元素的数据结构
7.4 并查集