LL(1)文法:从文法的开始符,向下推导,推出句子。
对文法G的句子进行确定的自顶向下语法分析的充分必要条件是,G的任意两个具有相同左部的
产生式A—>α|β 满足下列条件:
(1)如果α、β均不能推导出ε,则 FIRST(α) ∩ FIRST(β) = ∅。
(2)α 和 β 至多有一个能推导出 ε。
(3)如果 β *═> ε,则 FIRST(α) ∩ FOLLOW(A) = ∅。
将满足上述条件的文法称为LL(1)文法。
一、消除左递归
由于自上而下的分析方法不允许文法含有左递归。
因此对于包含直接左递归和间接左递归的文法都要消除左递归。
直接消除左递归比较容易。
例如:
P->Pa | b
直接消除左递归
P->bP'
P'->aP' | ε
二、提左因子
如果不提左因子,当面临两个相同的前缀,不知道选择哪条,必然会产生回溯。为了消除回溯,我们需要提左因子。
例如
三、实验
已知算术表达式文法 G[E]:
E → T E'
E' → + T E'|ε
T → F T'
T' → * F T'|ε
F → ( E )|i
判断该文法是否为 LL(1)文法,计算 FIRST 集合和 FOLLOW 集合
SELECT(E→T E')= FIRST(T)= {(, i}
SELECT(E'→+ T E')= {+}
SELECT(E'→ε)= FOLLOW(E')= {), #}
SELECT(T→F T')= FIRST(F)= {(, i}
SELECT(T' →* F T')= {*}
SELECT(T'→ε)= FOLLOW(T')= {+, ), #}
SELECT(F → ( E ))= {(}
SELECT(F → i)= {i}
具有相同左部产生式的 SELECT 集合交集为空
SELECT(E'→+ T E')∩SELECT(E'→ε)= {+}∩{), #}=Φ
SELECT(T' →* F T')∩SELECT(T'→ε) = {*}∩{+, ), #}=Φ
SELECT(F → ( E ))∩SELECT(F → i) = {(}∩{i}=Φ
所以,转换后的文法是 LL(1)文法。
此外,我们构造LL(1)分析表
表1-1 LL(1)分析表
|
i |
+ |
* |
( |
) |
# |
|
|
E |
E->TE’ |
E->TE’ |
||||
|
E’ |
E’->+TE’ |
E’->ε |
E’->ε |
|||
|
T |
T->FT’ |
T->FT’ |
||||
|
T’ |
T’->ε |
T’->*FT’ |
T’->ε |
T’->ε |
||
|
F |
F->i |
F->(E) |
程序如下:
1 #include<bits/stdc++.h> 2 #define ROW 6 3 #define COLUMN 9 4 using namespace std; 5 string table[ROW][COLUMN]={ 6 {"","(",")","*","+","-","/","i","#"}, 7 {"E","Te","","","","","","Te",""}, 8 {"e","","ε","","+Te","-Te","","","ε"}, 9 {"T","Ft","","","","","","Ft",""}, 10 {"t","","ε","*Ft","ε","ε","/Ft","","ε"}, 11 {"F","(E)","","","","","","i",""}}; 12 string Get_table(string x,string a){ 13 string ans=""; 14 for(int i=0;i<ROW;i++){ 15 for(int j=0;j<COLUMN;j++){ 16 if(x==table[i][0]&&a==table[0][j]){ 17 ans=table[i][j]; 18 return ans; 19 } 20 } 21 } 22 return ans; 23 } 24 bool check_LL1(string input){ 25 bool flag=true; 26 stack < string > s; 27 s.push("#"); 28 s.push("E"); 29 int i=0; 30 string a=input.substr(i,1); 31 string x; 32 while(flag){ 33 string RS; 34 x=s.top(); 35 if(x==a && a=="#"){ 36 break; 37 }else if(x==a && a!="#"){ 38 s.pop(); 39 i++; 40 a=input.substr(i,1); 41 }else if((RS=Get_table(x,a))!=""){ 42 if(RS!="ε"){ 43 s.pop(); 44 for(int j=RS.length()-1;j>=0;j--){ 45 string tmp=RS.substr(j,1); 46 s.push(tmp); 47 } 48 }else{ 49 s.pop(); 50 } 51 }else{ 52 flag=false; 53 break; 54 } 55 } 56 return flag; 57 } 58 int main(){ 59 string input; 60 while(cin>>input){ 61 input=input+"#"; 62 if(check_LL1(input)){ 63 cout<<"correct"<<endl; 64 }else{ 65 cout<<"error"<<endl; 66 } 67 } 68 return 0; 69 }
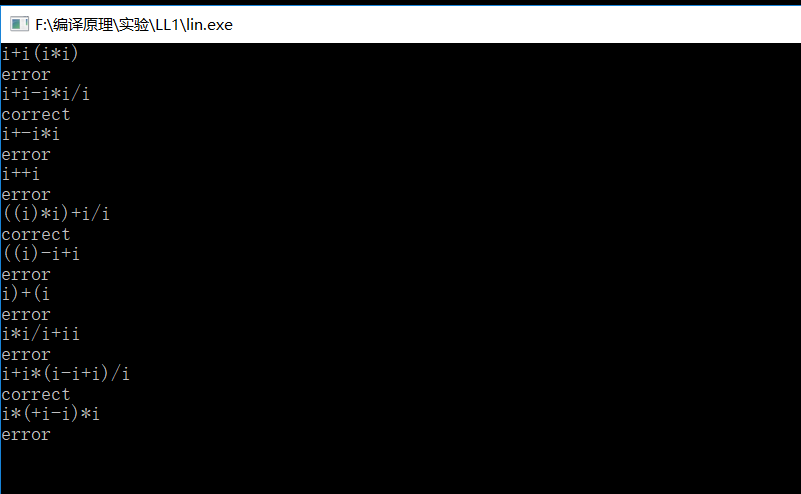
实验截图: