Logistics Regression (对数几率回归)及numpy实现

Logistics Regression

我们知道线性回归模型可以处理回归问题，但是如何处理分类问题？

对于一个二分类问题，或许我们可以认为w*x+b > 0为正类，其他情况为负类。

那么模型不就变成了：y =  f(z)  ,z = w*x+b,即 y = f(w*x+b)

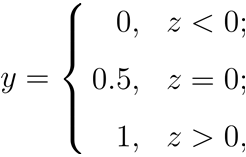
z大于零就判为正例，小于零就判为反例，z为临界值零则可任意判别 。

不难发现我们提出了一个新的函数 f ，也就是阶跃函数作为一个联系函数，把 z = w*x+b一个线性模型和 y 联系起来了。

于是我们把这种加入了联系函数的新的线性模型称之为广义线性模型。

广义线性模型的一般形式为：

 　　在这里，g 称为联系函数，因此我们刚才说的 f 是联系函数是有点区别的，f 函数应该是 g 的反函数，g 是关于y 的一个函数，也就 g(y) = w*x+b，不难发现，广义线性模型的目的是希望用线性模型w*x+b来逼近y 的衍生物 g(y)。

Why  logistic ?

　　从阶跃函数的图像上看，不难发现它是一个不是一个严格单调的函数（ps：西瓜书上说是因为连续，并未说明要求单调，但是笔者认为是因为不是严格单调所以才不能使用阶跃函数），因此不能作为 g 的反函数。于是我们想引入一个单调可微的函数，sigmoid函数。

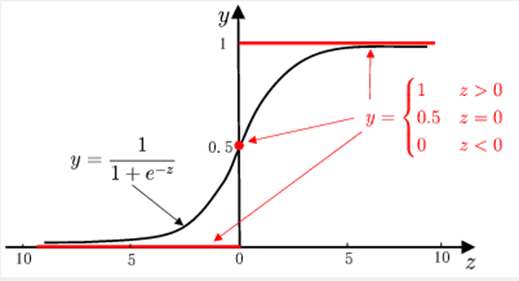
 所以 ：

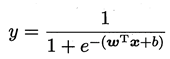
 若将 y 视为样本 x 下作为正例的可能性，则1-y 则是负例的可能性（这里其实我们使用了一个假设，在给定x的情况下y服从Bernoulli分布）。我们称

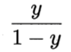
为几率（odds） ，几率反映了x作为正例的相对可能性，对几率取对数得到对数几率（log odds，也称 logit）：

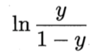
此处我们进行一番推导：

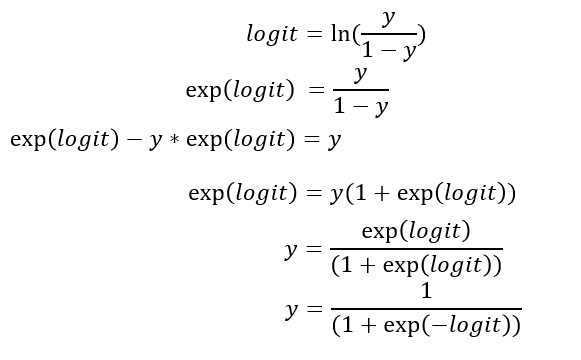
 至此，我们发现对数几率 logit 和 y 的关系是sigmoid函数关系，这也是开头为什么我们要用sigmoid函数原因。

 接着我们根据这个式子，我们提出假设： 对数几率 logit 和 x 满足线性相关，即 logit = w*x+b。

 因此呼应了我们提出的对数几率回归模型，使用sigmoid函数作为联系函数，用线性模型去逼近真实的对数几率。

 

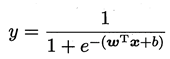
因此这就是为什么该模型称为对数几率回归模型。

当我们不知道数据分布的情况下，我们得到的模型输出不仅仅是预测的类别，而是近似的概率。

什么时候能够确定我们的输出是概率呢？

需要满足两个条件：

1.  y服从Bernoulli分布（只有分类问题0,1值，经常会选择该假设。该假设的意义在于对每一个确定的x，y仍然是一个随机变量，给出的x不同，y服从的Bernoulli分布参数也不同）

2.  对数几率 logit 和 x 满足线性相关。

 只有这两个条件满足输出的才是概率，否则输出的是一种近似概率的置信度。

代码实现：

数据集：德国信用数据集：UCI German Credit

训练集和测试集按9:1划分。

笔者没有进行特征归一化的测试结果准确率是64%，归一化后，同一个验证集上准确率达到了73%，数据归一化确实提升了模型的泛化能力。

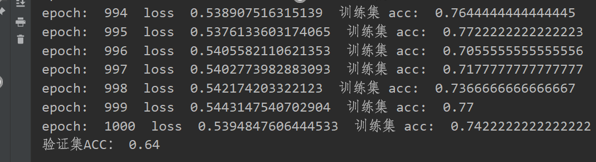
代码如下：

import numpy as np
import math

class LR(object):
    def __init__(self,nums_feature,lr = 0.001,batch = 32,epoch=1000):
        self.lr=lr
        self.nums_class = 2 # y的分类数，这里只有二分类，所以是2
        self.nums_feature = nums_feature # x 的特征数
        self.w = np.random.normal(0, 1,nums_feature).reshape(nums_feature,1)
        self.b = np.zeros(1)
        self.batch_size = batch
        self.epoch = epoch

    def sigmoid(self,x):
        return 1 / (1 + np.exp(-x))

    def delta_sigmoid(self,x): # sigmoid 导数
        s = self.sigmoid(x)
        return (1-s)*s

    def calculate_loss(self,xx,yy):
        # xx shape: nums*f
        # yy shape: nums*1
        nums = xx.shape[0]
        mat = np.matmul(xx, self.w) + self.b.repeat(nums).reshape(nums,1)
        # mat shape : nums*1
        loss = (np.log(1+np.exp(mat))-mat*yy).sum()
        return loss/nums # float

    def get_grad(self,xx,yy):
        nums = xx.shape[0]
        mat = np.matmul(xx, self.w)+self.b.repeat(nums).reshape(nums,1)
        active_mat = self.sigmoid(mat)
        delta = np.repeat(yy - active_mat,repeats= self.nums_feature).reshape(nums,self.nums_feature)
        w_grad = delta*xx
        w_grad = -1*np.sum(w_grad,axis=0)/nums
        b_grad = -1*(yy - active_mat).sum()/nums
        return w_grad.reshape(self.nums_feature,1) , b_grad

    def fit(self,X,Y):
        # 输入X，Y为numpy的格式
        samples_num = X.shape[0]
        SX = X
        SY = Y
        Y = Y.reshape(samples_num,1)
        for epoch in range(1,self.epoch+1):
            shuffle_ix = np.random.permutation(np.arange(samples_num))
            X = X[shuffle_ix] # nums*f
            Y = Y[shuffle_ix] # nums*1
            loss = 0.0
            for idx in range(0,samples_num,self.batch_size):
                xx = X[idx:idx+self.batch_size]
                yy = Y[idx:idx+self.batch_size]
                loss = loss + self.calculate_loss(xx,yy)
                w_grad,b_grad = self.get_grad(xx,yy) # 计算梯度
                self.w = self.w - self.lr*w_grad # w 权值更新
                self.b = self.b - self.lr*b_grad # b 权值更新
            acc= self.predict(SX,SY)
            print('epoch: ',epoch,' loss ',loss/(samples_num//self.batch_size),' 训练集 acc: ',acc)
        pass

    def predict(self,X,Y):
        nums = X.shape[0]
        prey = self.sigmoid(np.matmul(X, self.w) + self.b.repeat(nums).reshape(nums,1)).squeeze()
        pre_label = np.where(prey > 0.5,1,0)
        acc = np.where(pre_label==Y,1,0).sum()
        return acc/nums

np.random.seed(123)
data = np.loadtxt("german.data-numeric")
print(data)
# 数据归一化
# n, l = data.shape
# for j in range(l-1):
#     meanVal = np.mean(data[:, j])
#     stdVal = np.std(data[:, j])
#     data[:, j] = (data[:, j]-meanVal) / stdVal

shuffle_ix = np.random.permutation(np.arange(data.shape[0])) # 打乱数据集
data = data[shuffle_ix]
X = data[:900,:-1]
Y = data[:900,-1]-1 # Y label = 1 or 2 , Y = Y-1 get label = 0 or 1
print(data.shape)
print(X.shape)
print(Y.shape)
LR = LR(24)
LR.fit(X,Y)
X =data[900:,:-1]
Y =data[900:,-1] -1
print('验证集ACC：',LR.predict(X,Y))

参考资料：

1、周志华——《机器学习》

2、逻辑回归输出的值是真实的概率吗？——https://www.jianshu.com/p/a8d6b40da0cf

3、李航——《统计学习方法》

4、实战-logistic 回归二元分类——https://zhuanlan.zhihu.com/p/99473017