四元数和欧拉角，轴角对之间的相互转化

 

                                在3D图形学中，最常用的旋转表示方法便是四元数和欧拉角，比起矩阵来具有节省存储空间和方便插值的优点。本文主要归纳了两种表达方式的转换，计算公式采用3D笛卡尔坐标系：

                                                                                                          

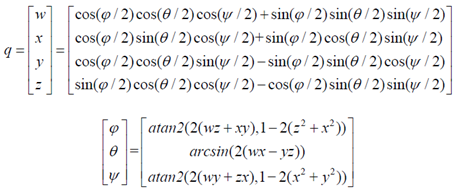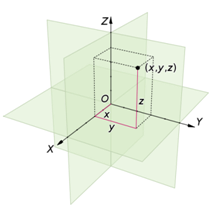
                                                                                               图1 3D Cartesian coordinate System (from wikipedia)

                                定义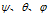分别为绕Z轴、Y轴、X轴的旋转角度，如果用Tait-Bryan angle表示，分别为Yaw、Pitch、Roll。

                                                                                                             

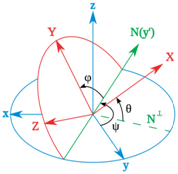
                                                                                                     图2 Tait-Bryan angles (from wikipedia)

                              一、四元数的定义

                                                                                                              

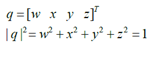
                                  通过旋转轴和绕该轴旋转的角度可以构造一个四元数       ：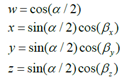

                                  其中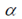是绕旋转轴旋转的角度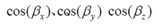，为旋转轴在x,y,z方向的分量（由此确定了旋转轴）。

                             二、欧拉角到四元数的转换

                                                                                         

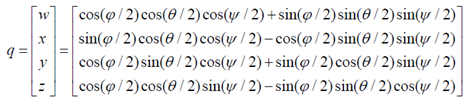
                              三、四元数到欧拉角的转换

                                                                                         

                                               arctan和arcsin的结果是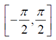，这并不能覆盖所有朝向(对于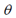角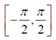的取值范围已经满足)，因此需要用atan2来代替arctan。

                                                                                  

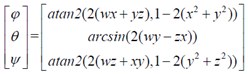
                            四、在其他坐标系下使用

                                                 在其他坐标系下，需根据坐标轴的定义，调整一下以上公式。如在Direct3D中，笛卡尔坐标系的X轴变为Z轴，Y轴变为X轴，Z轴变为Y轴（无需考虑方向）。