Nim游戏
https://www.acwing.com/problem/content/893/
分析:
谁进行最后一次,谁就赢。那么先手面对异或和为0就是必败局面(因为后手已经进行到了必胜局面,将最后的石子给那完了)
所以,异或和为0,先手必输,否则,先手必胜。
代码:

1 #include <iostream> 2 3 using namespace std; 4 5 int ans, n, x; 6 int main() 7 { 8 cin >> n; 9 while (n -- ) 10 { 11 cin >> x; 12 ans ^= x; 13 } 14 if (ans) cout << "Yes" << " "; 15 else cout << "No" << " "; 16 return 0; 17 }
台阶-Nim游戏
链接:https://www.acwing.com/problem/content/894/
分析:
我们可以在任意台阶上,拿任意颗石子放到它的下一个台阶,但拿到地面上的石子就不能再拿了。谁无法操作谁输(谁最后一个拿,谁赢)。
结论为:若奇数台阶上的石子异或和为0,则先手必败,否则,先手必胜。
证明:如果异或和不为0, 先手第一次拿石子后,将局面变为异或和为0,再那之后,先手总是将必败局面留给了后手(异或和为0,为必败局面,因为当你面对异或和为0,到了结局,队手将石子全放到了地面上)。
如果先手已经给后手造成了必败局面,那么后手如果拿偶数上的石子放到奇数层,我们将这些石子再拿到下一个偶数层。如果后手拿了奇数上的石子,有Nim游戏(上一题),使奇数层异或和为x,我们可以找到一个a[i]从中拿出(a[i] - x)个石子。
使局面再次变为必败局面留给后手。
思考:
为什么不能采用偶数层异或和呢?
现在,假设我们处于必胜局面,我们通过拿出若干个石子,试的局面变成了必败局面,也就是偶数层异或和为0,这时,后手将第一层(这是奇数层)的石子,全部拿到地面上,!!!注意,这时,局面还是必败局面,先手却面临了必败局面,因为后手将第一层放到地面上,对我们的偶数层异或和没有影响,还是异或和为0,但先手却面临着必败局面,而且还不能改变局面,因为第一层已经没有了石子了,这个时候,先手只能破坏异或和为0的局面,
代码:

1 #include <iostream> 2 3 using namespace std; 4 5 // const int N = 6 7 int main() 8 { 9 int ans = 0; 10 int n; cin >> n; 11 for (int i = 1; i <= n; i ++ ) 12 { 13 int x; scanf("%d", &x); 14 if (i & 1) ans ^= x; 15 } 16 if (ans) cout << "Yes" << " "; 17 else cout << "No" << " "; 18 19 return 0; 20 }
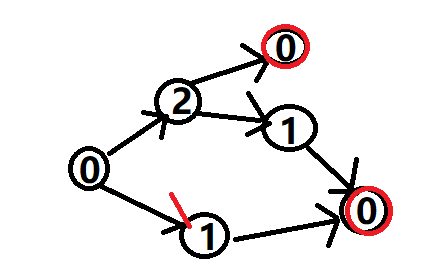
集合-Nim游戏
链接:https://www.acwing.com/problem/content/895/
分析:
用到了SG函数
如果SG(x)等与0,一定是一个必败局面,
SG(x)为0,先手必败,SG(x)不为0,先手必胜
可以以这个图为例 。
如果n副图的异或和为0的话,则是一个先手必败局面,否则就是一个先手必胜局面,这已经不需要再分析了。
终止状态定义为0,其他所有sg的值定义成当前状态不能到达的状态的最小自然数是多少。
代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const int N = 110, M = 10010; 6 7 int n, k; 8 int a[N], f[M]; 9 10 int sg(int x) 11 { 12 if (f[x] != -1) return f[x]; 13 14 unordered_set<int> st; 15 for (int i = 1; i <= k; i ++ ) 16 { 17 int sum = a[i]; 18 if (x >= sum) st.insert(sg(x - sum)); 19 } 20 21 for (int i = 0; ; i ++ ) 22 if (!st.count(i)) return f[x] = i; 23 } 24 int main() 25 { 26 cin >> k; 27 for (int i = 1; i <= k; i ++ ) 28 { 29 cin >> a[i]; 30 } 31 32 int ans = 0; 33 cin >> n; 34 memset(f, -1, sizeof f); 35 for (int i = 0; i < n; i ++ ) 36 { 37 int x; cin >> x; 38 ans ^= sg(x); 39 } 40 41 if (ans) cout << "Yes" << " "; 42 else cout << "No" << " "; 43 44 return 0; 45 }
拆分-Nim游戏
链接: https://www.acwing.com/problem/content/896/
分析:
这题目题意不清。。。
题目说是,可以从一个大的堆里面拿出若干个,可以放入两个更小的石堆里面,而且还能多放点,比如从大堆里拿了5个,可以向一堆放5个,可以给另一堆也放5个,放4个,... ,放0个。
代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const int N = 110; 6 7 int n; 8 int f[N]; 9 10 int sg(int x) 11 { 12 if (f[x] != -1) return f[x]; 13 14 unordered_set<int> st; 15 for (int i = 0; i < x; i ++ ) 16 for (int j = 0; j <= i; j ++ ) 17 st.insert(sg(i) ^ sg(j)); 18 19 for (int i = 0; ; i ++ ) 20 if (!st.count(i)) //count(x)返回x的个数 21 return f[x] = i; 22 } 23 int main() 24 { 25 cin >> n; 26 27 memset(f, -1, sizeof f); 28 int ans = 0; 29 while (n -- ) 30 { 31 int x; cin >> x; 32 ans ^= sg(x); 33 } 34 35 if (ans) cout << "Yes" << " "; 36 else cout << "No" << " "; 37 38 return 0; 39 }
移棋子游戏
链接:https://www.acwing.com/problem/content/1321/
分析:
则就是sg函数的模板题了。
只需要将每个棋子的sg函数求出来异或一下就OK了。
代码:

1 #include <iostream> 2 #include <unordered_set> 3 #include <cstring> 4 5 using namespace std; 6 7 const int N = 2010, M = 6010; 8 9 int n, m, k; 10 int h[N], e[M], ne[M], tot; 11 int f[M]; 12 13 void add(int a, int b) 14 { 15 e[++ tot] = b, ne[tot] = h[a], h[a] = tot; 16 } 17 18 int sg(int x) 19 { 20 if (f[x] != -1) return f[x]; 21 22 unordered_set<int> st; 23 for (int i = h[x]; ~i; i = ne[i]) 24 { 25 int y = e[i]; 26 st.insert(sg(y)); 27 } 28 29 for (int i = 0; ; i ++ ) 30 if (!st.count(i)) return f[x] = i; 31 } 32 33 int main() 34 { 35 cin >> n >> m >> k; 36 37 memset(h, -1, sizeof h); 38 memset(f, -1, sizeof f); 39 for (int i = 0; i < m; i ++ ) 40 { 41 int x, y; cin >> x >> y; 42 add(x, y); 43 } 44 45 int ans = 0; 46 for (int i = 0; i < k; i ++ ) 47 { 48 int x; cin >> x; 49 ans ^= sg(x); 50 } 51 52 if (ans) cout << "win" << " "; 53 else cout << "lose" << " "; 54 55 return 0; 56 }
取石子【难】
链接:https://www.acwing.com/problem/content/1323/
分析:
完全不知道该怎么想,正解是,让a表示只有一颗石子的堆数,让b表示每堆石子数大于1个的 石子数+堆数-1.
然后,必胜局面是b为奇数。
按照yxc说法,奇数状态必存在一种方式,到达偶数状态,而偶数状态只能转向奇数状态,最后,先手面对一堆一个石子,就赢了。
分为五种情况:用f[a][b]表示关系
f[a-1][b],从a中取出一个石子(a大于0)
f[a][b-1],从b中取出一个石子(b大于0)
f[a][b-1],和并b中两堆(b大于1)
f[a-2][b+3],合并a中两个(a大于1)
f[a-1][b+1],合并a中的一个和b中的一堆
代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 using namespace std; 5 6 const int N = 55, M = 50050; 7 8 int f[N][M]; 9 10 int dp(int a, int b) 11 { 12 int &x = f[a][b]; 13 if (x != -1) return x; 14 if (!a) return x = b % 2;//a等于0,只要看b是否为奇数就好了 15 if (b == 1) return dp(a + 1, 0); 16 //b只有一堆,这一堆里只有一个,所以,它可以算入一个a了 17 18 if (a && !dp(a - 1, b)) return x = 1; 19 if (b && !dp(a, b - 1)) return x = 1; 20 if (a >= 2 && !dp(a - 2, b + (b ? 3 : 2))) return x = 1; 21 if (a && b && !dp(a - 1, b + 1)) return x = 1; 22 23 return x = 0; 24 } 25 int main() 26 { 27 memset(f, -1, sizeof f); 28 29 int T; cin >> T; 30 while (T -- ) 31 { 32 int n; cin >> n; 33 int a = 0, b = 0; 34 for (int i = 0; i < n; i ++ ) 35 { 36 int x; cin >> x; 37 if (x == 1) a ++; 38 else b += b ? x + 1 : x;//第一次,一堆,x个,其他,加一个堆数,加x的个数 39 } 40 41 if (dp(a, b)) cout << "YES" << " "; 42 else cout << "NO" << " "; 43 } 44 45 return 0; 46 }
取石子游戏【超难】
链接:https://www.acwing.com/problem/content/1324/
捡石头:
链接:https://ac.nowcoder.com/acm/problem/14388
分析:
谁是最后一个,谁就赢。
如果n % (m + 1) == 0,那么先手必败,因为不管先手拿多少石头,后手都可以凑出来m + 1。这样,一直到最后。
如果n % (m + 1) != 0,那么后手必败,因为第一次先手先拿,然后后手再拿,然后先手就可以凑出来m+1,然后持续到最后。
代码:

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <algorithm> 5 #include <cmath> 6 #include <iomanip> 7 #include <limits.h> 8 #include <sstream> 9 #include <cctype> 10 #include <numeric> 11 #include <vector> 12 #include <queue> 13 #include <deque> 14 #include <stack> 15 #include <map> 16 #include <unordered_map> 17 #include <unordered_set> 18 #include <set> 19 //#pragma GCC optimize(2) 20 //#pragma GCC optimize(3, "Ofast", "inlin") 21 22 using namespace std; 23 24 #define ios ios::sync_with_stdio(false) , cin.tie(0) 25 #define x first 26 #define y second 27 28 typedef long long LL; 29 typedef unsigned long long ULL; 30 typedef pair<int, int> PII; 31 32 const int N = 100010, INF = 0x3f3f3f3f, mod = 1e9 + 7, base = 131; 33 const double eps = 1e-6, PI = acos(-1); 34 35 int n, m; 36 37 void work() 38 { 39 cin >> n >> m; 40 41 if (n <= m) puts("first"); 42 else 43 { 44 if (n % (m + 1) == 0) puts("second"); 45 else puts("first"); 46 } 47 } 48 49 int main() 50 { 51 //ios; 52 int T = 1; 53 // cin >> T; 54 while (T -- ) 55 { 56 work(); 57 } 58 59 return 0; 60 }
小牛vs小客:
https://ac.nowcoder.com/acm/problem/15065
分析:
当n小于等于2的时候,很显然,XiaoNiu一定会赢,但是当n大于2的时候,不管先手怎么办,后手都可以将剩下的石子分为偶数部分,所以后手必赢
代码:

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <algorithm> 5 #include <cmath> 6 #include <iomanip> 7 #include <limits.h> 8 #include <sstream> 9 #include <cctype> 10 #include <numeric> 11 #include <vector> 12 #include <queue> 13 #include <deque> 14 #include <stack> 15 #include <map> 16 #include <unordered_map> 17 #include <unordered_set> 18 #include <set> 19 //#pragma GCC optimize(2) 20 //#pragma GCC optimize(3, "Ofast", "inlin") 21 22 using namespace std; 23 24 #define ios ios::sync_with_stdio(false) , cin.tie(0) 25 #define x first 26 #define y second 27 28 typedef long long LL; 29 typedef unsigned long long ULL; 30 typedef pair<int, int> PII; 31 32 const int N = 100010, INF = 0x3f3f3f3f, mod = 1e9 + 7, base = 131; 33 const double eps = 1e-6, PI = acos(-1); 34 35 36 void work() 37 { 38 int n; 39 while (cin >> n) 40 { 41 if (n <= 2) cout << "XiaoNiu" << " "; 42 else cout << "XiaoKe" << " "; 43 } 44 } 45 46 int main() 47 { 48 //ios; 49 int T = 1; 50 // cin >> T; 51 while (T -- ) 52 { 53 work(); 54 } 55 56 return 0; 57 }
| 栗酱的异或和 |
分析:
NIM游戏,这里,第k堆是先要选的,也是必选的,是先手要选的。同时,谁先不能取谁就输了,也就是谁最后一个取,谁就赢了。
如果不考虑第一次要选k的话,异或和为0,先手必败(所有物品都被取光是一个必败局面,因为队友取走了最后一件物品,已经胜利了)。
那么这个时候,加上先选第k个物品的限制。
我们可以假设第一次取第k堆时,没有取,留到最后先手再取。
这样,我们将除了第k堆以外的石子异或起来,假设结果为x的话,这是就是先手所面临的局面,要将第k堆里取出若干个,将这x个石子全部消掉,消掉的话,就意味着,最后一次是先手拿完的(x=0的话,先手也要拿,因为先手必须要拿第k堆至少一个石子,不能不拿,这个时候,可以将第k堆全部拿了就可以了)。但是,如果x大于第k堆的数量,就没办法拿了,当x等于第k堆的数量的时候,
这样,我们将除了第k堆以外的石子异或起来,假设结果为x的话,我们的目的就是让异或的结果不为0,所以,如果第k堆的石子数大于x的话,那么,我们去掉a[k] - x个石子就可以了,先手拿掉(a[k]-x)个石子,让所有石子的异或和为0,将必败局面丢给了后手。
代码:

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <algorithm> 5 #include <cmath> 6 #include <iomanip> 7 #include <limits.h> 8 #include <sstream> 9 #include <cctype> 10 #include <numeric> 11 #include <vector> 12 #include <queue> 13 #include <deque> 14 #include <stack> 15 #include <map> 16 #include <unordered_map> 17 #include <unordered_set> 18 #include <set> 19 //#pragma GCC optimize(2) 20 //#pragma GCC optimize(3, "Ofast", "inlin") 21 22 using namespace std; 23 24 #define ios ios::sync_with_stdio(false) , cin.tie(0) 25 #define x first 26 #define y second 27 28 typedef long long LL; 29 typedef unsigned long long ULL; 30 typedef pair<int, int> PII; 31 32 const int N = 100010, INF = 0x3f3f3f3f, mod = 1e9 + 7, base = 131; 33 const double eps = 1e-6, PI = acos(-1); 34 35 int n, k; 36 int a[N]; 37 38 void work() 39 { 40 cin >> n >> k; 41 int ans = 0; 42 for (int i = 1; i <= n; i ++ ) 43 { 44 cin >> a[i]; 45 if (i == k) continue; 46 ans ^= a[i]; 47 } 48 // cout << ans << endl; 49 // cout << (ans ^ a[k]) << " "; 50 if (ans < a[k]) cout << "Yes" << " "; 51 else cout << "No" << " "; 52 } 53 54 int main() 55 { 56 //ios; 57 int T = 1; 58 cin >> T; 59 while (T -- ) 60 { 61 work(); 62 } 63 64 return 0; 65 }