数据结构题锦——树链

树链：

树链求最近公共祖先

最近公共祖先

题目：

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 N,M,S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 N−1 行每行包含两个正整数x,y，表示 x 结点和 y 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 M 行每行包含两个正整数a,b，表示询问 a 结点和 b 结点的最近公共祖先。

输出格式

输出包含 M 行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入 #1复制

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出 #1复制

4
4
1
4
4

说明/提示

对于 30% 的数据，N≤10，M≤10。

对于 70% 的数据，N≤10000，M≤10000。

对于 100% 的数据，N≤500000，M≤500000。

样例说明：

该树结构如下：

第一次询问：2,4 的最近公共祖先，故为 4。

第二次询问：3,2 的最近公共祖先，故为 4。

第三次询问：3,5 的最近公共祖先，故为 1。

第四次询问：1,2 的最近公共祖先，故为 4。

第五次询问：4,5 的最近公共祖先，故为 4。

故输出依次为 4, 4, 1, 4, 4。

分析：

LCA：

树上倍增法可以做，树链也可以做

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 500005, M = N << 1;
int n, m, root;
int w[N], h[N], e[M], ne[M], idx;
int dep[N], fa[N], sz[N], son[N];
int id[N], nw[N], top[N], tot;
void add(int a, int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int x, int father, int depth)
{
  dep[x] = depth, fa[x] = father, sz[x] = 1;
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == father) continue;
    dfs1(y, x, depth + 1);
    sz[x] += sz[y];
    if (sz[son[x]] < sz[y]) son[x] = y;
  }
}
void dfs2(int x, int t)
{
  id[x] = ++ tot, nw[tot] = w[x], top[x] = t;
  if (!son[x]) return;
  dfs2(son[x], t);
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == fa[x] || y == son[x]) continue;
    dfs2(y, y);
  }
}
int lca(int u, int v)
{
  while (top[u] != top[v])
  {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) swap(u, v);
  return v;
}
int main()
{
  memset(h, -1, sizeof h);
  scanf("%d%d%d", &n, &m, &root);
  for (int i = 0; i < n - 1; i ++ )
  {
    int a, b; scanf("%d%d", &a, &b);
    add(a, b); add(b, a);
  }
  dfs1(root, -1, 1);
  dfs2(root, root);
  while (m -- )
  {
    int x, y; scanf("%d%d", &x, &y);
    printf("%d
", lca(x, y));
  }
  return 0;
}

　

2568. 树链剖分

题目：

给定一棵树，树中包含 nn 个节点（编号 1∼n），其中第 ii 个节点的权值为 ai。

初始时，1 号节点为树的根节点。

现在要对该树进行 m 次操作，操作分为以下 4种类型：

• 1 u v k，修改路径上节点权值，将节点 u 和节点 v、v 之间路径上的所有节点（包括这两个节点）的权值增加 kk。
• 2 u k，修改子树上节点权值，将以节点 u 为根的子树上的所有节点的权值增加 k。
• 3 u v，询问路径，询问节点 u 和节点 v 之间路径上的所有节点（包括这两个节点）的权值和。
• 4 u，询问子树，询问以节点 u 为根的子树上的所有节点的权值和。

输入格式

第一行包含一个整数 n，表示节点个数。

第二行包含 n 个整数，其中第 i 个整数表示 ai。

接下来 n− 行，每行包含两个整数 x,y，表示节点 x 和节点 y 之间存在一条边。

再一行包含一个整数 m，表示操作次数。

接下来 m 行，每行包含一个操作，格式如题目所述。

输出格式

对于每个操作 3 和操作 4，输出一行一个整数表示答案。

数据范围

1≤n,m≤105,
0≤ai,k≤105,
1≤u,v,x,y≤n

输入样例：

5
1 3 7 4 5
1 3
1 4
1 5
2 3
5
1 3 4 3
3 5 4
1 3 5 10
2 3 5
4 1

输出样例：

16
69

　

分析：

树上任意两点之间查询和修改，对整棵子树进行查询和修改

树链+线段树

树链可以将一棵树转化成序列，使得树中任意一条路径可以分割成不超过logn段连续的序列。

如果是对一个子树求改和查询的话，就是对子树根节点维护，因为DFS在搜索的时候，就是一颗一颗子树搜索的，所以，一棵子树内的序列好是连续的

然后，问题就转化为了对连续区间的查询和修改，用线段树维护

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010, M = N << 1;
int n, m;
int w[N], h[N], e[M], ne[M], idx;
int id[N], nw[N], tot;
int dep[N], sz[N], top[N], fa[N], son[N];
struct Node{
  int l, r;
  ll add, sum;
}tr[N << 2];
void add(int a, int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int x, int father, int depth)
{
  dep[x] = depth, fa[x] = father, sz[x] = 1;
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == father) continue;
    dfs1(y, x, depth + 1);
    sz[x] += sz[y];
    if (sz[son[x]] < sz[y]) son[x] = y;
  }
}
void dfs2(int x, int t)
{
  //重链的top一定是一个轻儿子
  id[x] = ++ tot, nw[tot] = w[x], top[x] = t;
  if (!son[x]) return;
  dfs2(son[x], t);
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == fa[x] || y == son[x]) continue;
    dfs2(y, y);
  }
}
void pushup(int u)
{
  tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
  Node &c = tr[u], &a = tr[u << 1], &b = tr[u << 1 | 1];
  if (c.add)
  {
    a.sum += c.add * (a.r - a.l + 1);
    a.add += c.add;
    b.sum += c.add * (b.r - b.l + 1);
    b.add += c.add;
    c.add = 0;
  }
}
void build(int u, int l, int r){
  if (l == r)
  {
    tr[u] = {l, r, 0, nw[l]};
    return;
  }
  tr[u] = {l, r};
  int mid = l + r >> 1;
  build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
  pushup(u);
}
void update(int u, int l, int r, int c)
{
  if (tr[u].l >= l && tr[u].r <= r)
  {
    tr[u].sum += (tr[u].r - tr[u].l + 1) * c;
    tr[u].add += c;
    return;
  }
  pushdown(u);
  int mid = tr[u].l + tr[u].r >> 1;
  if (l <= mid) update(u << 1, l, r, c);
  if (r > mid) update(u << 1 | 1, l, r, c);
  pushup(u);
}
ll query(int u, int l, int r)
{
  if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
  pushdown(u);
  ll res = 0;
  int mid = tr[u].l + tr[u].r >> 1;
  if (l <= mid) res += query(u << 1, l, r);
  if (r > mid) res += query(u << 1 | 1, l, r);
  return res;
}
void update_path(int u, int v, int c)
{
  //给路径从u到v都+c，显然分为在同一重链和不在同一重链上
  //top不同，表明不在同一重链上
  while (top[u] != top[v])
  {
    //让u的重链的头结点在下面
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    //更新u的从u位置一直到top[u]，注意，DFS序前者大后者小
    update(1, id[top[u]], id[u], c);
    u = fa[top[u]];
  }
  //找到u和v更新到在同一条重链上
  if (dep[u] < dep[v]) swap(u, v);
  update(1, id[v], id[u], c);
}
ll query_path(int u, int v)
{
  ll res = 0;
  while (top[u] != top[v])
  {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    res += query(1, id[top[u]], id[u]);
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) swap(u, v);
  res += query(1, id[v], id[u]);
  return res;
}
void update_tree(int u, int c)
{
  //因为DFS是一棵子树搜完在搜其他子树，所以，一棵子树内的所有节点的DFS序是一段连续的区间
  update(1, id[u], id[u] + sz[u] - 1, c);
}
ll query_tree(int u)
{
  return query(1, id[u], id[u] + sz[u] - 1);
}
int main()
{
  scanf("%d", &n);
  for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
  memset(h, -1, sizeof h);
  for (int i = 0; i < n - 1; i ++ )
  {
    int a, b; scanf("%d%d", &a, &b);
    add(a, b); add(b, a);
  }
  dfs1(1, -1, 1);
  dfs2(1, 1);
  build(1, 1, n);
  scanf("%d", &m);
  while (m -- )
  {
    int t, u, v, k;
    scanf("%d%d", &t, &u);
    if (t == 1)
    {
      scanf("%d%d", &v, &k);
      update_path(u, v, k);
    }
    else if (t == 2)
    {
      scanf("%d", &k);
      update_tree(u, k);
    }
    else if (t == 3)
    {
      scanf("%d", &v);
      printf("%lld
", query_path(u, v));
    }
    else
    {
      printf("%lld
", query_tree(u));
    }
  }
  return 0;
}

　　

 918. 软件包管理器

P2146 [NOI2015] 软件包管理器

Linux 用户和 OSX 用户一定对软件包管理器不会陌生。

通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。

Debian/Ubuntu 使用的 apt-get，Fedora/CentOS 使用的 yum，以及 OSX 下可用的 homebrew 都是优秀的软件包管理器。

你决定设计你自己的软件包管理器。

不可避免地，你要解决软件包之间的依赖问题。

如果软件包 A 依赖软件包 B，那么安装软件包 A 以前，必须先安装软件包 B。

同时，如果想要卸载软件包 B，则必须卸载软件包 A。

现在你已经获得了所有的软件包之间的依赖关系。

而且，由于你之前的工作，除0 号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而 0 号软件包不依赖任何一个软件包。

依赖关系不存在环（若有 m(m≥2) 个软件包 A1,A2,A3,…,Am，其中 A1 依赖 A2，A2 依赖 A3，A3 依赖 A4，……，Am−1 依赖 Am，而 Am 依赖 A1，则称这 m 个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

现在你要为你的软件包管理器写一个依赖解决程序。

根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。

注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为 00。

输入格式

输入文件的第 1 行包含 1 个正整数 n，表示软件包的总数。软件包从 0 开始编号。

随后一行包含 n−1 个整数，相邻整数之间用单个空格隔开，分别表示 1,2,3,…,n−2,n−1 号软件包依赖的软件包的编号。

接下来一行包含 1 个正整数 q，表示询问的总数。

之后 q 行，每行 1 个询问。询问分为两种：

• install x：表示安装软件包 xx
• uninstall x：表示卸载软件包 xx

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

输出格式

输出文件包括 qq 行。

输出文件的第 ii 行输出 11 个整数，为第 ii 步操作中改变安装状态的软件包数。

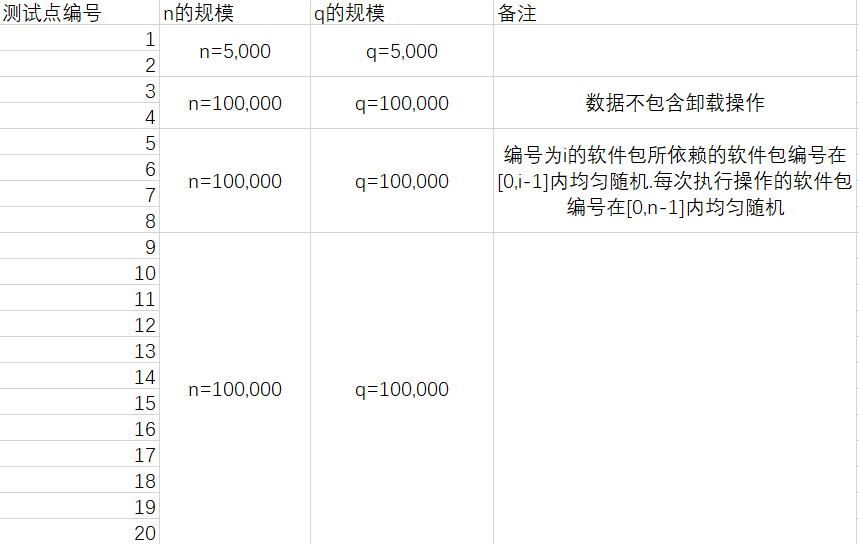
数据范围

输入样例1：

7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0

输出样例1：

3
1
3
2
3

输入样例2：

10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9

输出样例2

1
3
2
1
3
1
1
1
0
1

 

分析：

两种操作，

1：将根节点到当前节点的权值，全部变成1

2：将当前子树的权值，全部变成0

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int n, m;
int h[N], e[N], ne[N], idx;
int fa[N], son[N], sz[N], dep[N];
int id[N], top[N], tot;
struct Node{
    int l, r;
    int flag, sum;
}tr[N << 2];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int x, int depth)
{
    dep[x] = depth, sz[x] = 1;
    for (int i = h[x]; ~i; i = ne[i])
    {
        int y = e[i];
        dfs1(y, depth + 1);
        sz[x] += sz[y];
        if (sz[son[x]] < sz[y]) son[x] = y;
    }
}
void dfs2(int x, int t)
{
    id[x] = ++ tot, top[x] = t;
    if (!son[x]) return;
    dfs2(son[x], t);
    for (int i = h[x]; ~i; i = ne[i])
    {
        int y = e[i];
        if (y == son[x]) continue;
        dfs2(y, y);
    }
}
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
    Node &c = tr[u], &a = tr[u << 1], &b = tr[u << 1 | 1];
    if (c.flag != -1)
    {
        a.sum = c.flag * (a.r - a.l + 1);
        b.sum = c.flag * (b.r - b.l + 1);
        a.flag = b.flag = c.flag;
        c.flag = -1;
    }
}
void build(int u, int l, int r)
{
    if (l == r)
    {
        tr[u] = {l,r, -1, 0};
        return;
    }
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
    pushup(u);
}
void update(int u, int l, int r, int c)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].sum = c * (tr[u].r - tr[u].l + 1);
        tr[u].flag = c;
        return;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) update(u << 1, l, r, c);
    if (r > mid) update(u << 1 | 1, l, r, c);
    pushup(u);
}
int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    pushdown(u);
    int res = 0;
    int mid = tr[u].l + tr[u].l >> 1;
    if (l <= mid) res += query(u << 1, l, r);
    if (r > mid) res += query(u << 1 | 1, l, r);
    return res;
}
void update_path(int u, int v, int c)
{
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        update(1, id[top[u]], id[u], c);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) swap(u, v);
    update(1, id[v], id[u], c);
}
void update_tree(int u, int c)
{
    update(1, id[u], id[u] + sz[u] - 1, c);
}
int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 2; i <= n; i ++ )
    {
        int x; scanf("%d", &x);
        x ++;
        add(x, i);
        fa[i] = x;
    }
    dfs1(1, 1);
    dfs2(1, 1);
    build(1, 1, n);
    cin >> m;
    char op[20]; int x;
    while (m -- )
    {
        scanf("%s%d", op, &x);
        x ++;
        if (!strcmp(op, "install"))
        {
            int sum = query(1, 1, n);
            update_path(1, x, 1);
            int ans = query(1, 1, n) - sum;
            printf("%d
", ans);
        }
        else 
        {
            int sum = query(1, 1, n);
            update_tree(x, 0);
            int  ans = sum - query(1, 1, n);
            printf("%d
", ans);
        }
    }
    return 0;
}

　　

P2486 [SDOI2011]染色

题目：

题目描述

给定一棵 n 个节点的无根树，共有mm 个操作，操作分为两种：

1. 将节点 a 到节点 b 的路径上的所有点（包括 a 和 b）都染成颜色 c。
2. 询问节点 a 到节点 b 的路径上的颜色段数量。

颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成：11、222、1。

输入格式

输入的第一行是用空格隔开的两个整数，分别代表树的节点个数 n 和操作个数 m。

第二行有 n 个用空格隔开的整数，第 i 个整数wi​ 代表结点 i 的初始颜色。

第 3 到第 (n+1) 行，每行两个用空格隔开的整数 u,v，代表树上存在一条连结节点 u 和节点 v 的边。

第 (n+2) 到第 (n+m+1) 行，每行描述一个操作，其格式为：

每行首先有一个字符 op，代表本次操作的类型。

• 若 op 为 C，则代表本次操作是一次染色操作，在一个空格后有三个用空格隔开的整数 a,b,c，代表将 a 到 b 的路径上所有点都染成颜色 cc。
• 若 op 为 Q，则代表本次操作是一次查询操作，在一个空格后有两个用空格隔开的整数 a,b，表示查询 a 到 b 路径上的颜色段数量。

输出格式

对于每次查询操作，输出一行一个整数代表答案。

输入输出样例

输入 #1复制

6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

输出 #1复制

3
1
2

说明/提示

数据规模与约定

对于 100% 的数据，1≤n,m≤105，1≤wi​,c≤109，1≤a,b,u,v≤n，op 一定为 C 或 Q，保证给出的图是一棵树。

除原数据外，还存在一组不计分的 hack 数据。

分析：

树剖后，用线段树维护左端点l，右端点r，左端点颜色lc，右端点rc，区间更新颜色的标记tag，区间颜色的段树num。

现在对于维护线段树需要注意的是，在合并左子树和右子树的时候，左子树的右端点如果和右子树的左端点的颜色相同，那么，合并后的二叉线段树的num需要减一。

下面考虑树剖的问题， 如果当前树剖到的链与上一次的链在相交的边缘颜色可能相等，如果相等，答案需要减一。所以，统计答案的时候，需要记录一下上一次剖到的链的左端点的颜色（左端点指的是索引小的那头，也就是子树的树根位置），与当前树剖的右端点的颜色，比较两个颜色，如果相同则答案减一。

注意：由于u和v两个位置向上走，那么要记录ans1，ans2两个变量来存储上一次的左端点颜色。当top[u] = top[v]的时候，  已经在同一个重链上了，两边端点的颜色都要考虑与对应的ans比较颜色，相同答案要相应减一。

 代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int n, m;
int w[N],h[N], e[N << 1], ne[N << 1], idx;
int fa[N], son[N], sz[N], dep[N];
int id[N], nw[N], top[N], tot;
void add_edges(int a,int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int x, int father, int depth)
{
  dep[x] = depth, fa[x] = father, sz[x] = 1;
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == father) continue;
    dfs1(y, x, depth + 1);
    sz[x] += sz[y];
    if (sz[son[x]] < sz[y]) son[x] = y;
  }
}
void dfs2(int x, int t)
{
  id[x] = ++ tot, nw[tot] = w[x], top[x] = t;
  if (!son[x]) return;
  dfs2(son[x], t);
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == fa[x] || y == son[x]) continue;
    dfs2(y, y);
  }
}
struct Node{
  int l, r;
  int num, tag, lc, rc;
}tr[N << 2];
int Lc, Rc;
void pushup(int u)
{
  Node &c = tr[u], &a = tr[u << 1], &b = tr[u << 1 | 1];
  c.lc = a.lc, c.rc = b.rc;
  c.num = a.num + b.num;
  if (a.rc == b.lc) c.num --;
}
void pushdown(int u)
{
  Node &c = tr[u], &a = tr[u << 1], &b = tr[u << 1 | 1];
  if (c.tag)
  {
    a.num = b.num = c.num;
    a.lc = a.rc = b.lc = b.rc = c.lc;
    a.tag = b.tag = c.tag;
    c.tag = 0;
  }
}
void build(int u, int l, int r)
{
  tr[u] = {l, r, 0, 0, 0, 0};
  if (l == r) return;
  int mid = l + r >> 1;
  build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void update(int u, int l, int r, int c)
{
  if (tr[u].l == l && tr[u].r == r)
  {
    tr[u].tag = tr[u].num = 1;
    tr[u].lc = tr[u].rc = c;
    return;
  }
  pushdown(u);
  int mid = tr[u].l + tr[u].r >> 1;
  if (r <= mid) update(u << 1, l, r, c);
  else if (l > mid) update(u << 1 | 1, l, r, c);
  else update(u << 1, l, mid, c), update(u << 1 | 1, mid + 1, r, c);
  pushup(u);
}
int query(int u, int l, int r, int L, int R)
{
  if (tr[u].l == L)
    Lc = tr[u].lc;
  if (tr[u].r == R)
    Rc = tr[u].rc;
  if (tr[u].l == l && tr[u].r == r) return tr[u].num;
  pushdown(u);
  int mid = tr[u].l + tr[u].r >> 1;
  if (r <= mid) return query(u << 1, l, r, L, R);
  else if (l > mid) return query(u << 1 | 1, l, r, L, R);
  else
  {
    int ans = query(u << 1, l, mid, L, R) + query(u << 1 | 1, mid + 1, r, L, R);
    if (tr[u << 1].rc == tr[u << 1 | 1].lc) ans --;
    return ans;
  }
  pushup(u);
}
void update_path(int u, int v, int c)
{
  while (top[u] != top[v])
  {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    update(1, id[top[u]], id[u], c);
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) swap(u, v);
  update(1, id[v], id[u], c);
}
int query_path(int u, int v)
{
  int ans1 = -1, ans2 = -1;
  int ans = 0;
  while (top[u] != top[v])
  {
    if (dep[top[u]] < dep[top[v]]) swap(u, v), swap(ans1, ans2);
    ans += query(1, id[top[u]], id[u], id[top[u]], id[u]);
    //在swap后，ans1表示这颗树链下方的节点
    if (Rc == ans1) ans --;
    ans1 = Lc, u = fa[top[u]];
  }
  if (dep[u] < dep[v]) swap(u, v), swap(ans1, ans2);
  ans += query(1, id[v], id[u], id[v], id[u]);
  if (Rc == ans1) ans --;
  if (Lc == ans2) ans --;
  return ans;
}
int main()
{
  memset(h, -1, sizeof h);
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
  for (int i = 0; i < n - 1; i ++ )
  {
    int a, b; scanf("%d%d", &a, &b);
    add_edges(a, b);
    add_edges(b, a);
  }
  dfs1(1, -1, 1);
  dfs2(1, 1);
  // printf("-------------
");
  build(1, 1, n);
  for (int i = 1; i <= n; i ++ ) update(1, id[i], id[i], w[i]);
  char op[2]; int l, r, c;
  while (m -- )
  {
    scanf("%s%d%d", op, &l, &r);
    if (*op == 'C')
    {
      scanf("%d", &c);
      update_path(l, r, c);
    }
    else
    {
      printf("%d
", query_path(l, r));
    }
  }
}

　　

P2590 [ZJOI2008]树的统计

 题目：

题目描述

一棵树上有 n 个节点，编号分别为 1 到 n，每个节点都有一个权值 w。

我们将以下面的形式来要求你对这棵树完成一些操作：

I. CHANGE u t : 把结点 u 的权值改为 t。

II. QMAX u v: 询问从点 u 到点 v 的路径上的节点的最大权值。

III. QSUM u v: 询问从点 u 到点 v 的路径上的节点的权值和。

注意：从点 u 到点 v 的路径上的节点包括 u 和 v 本身。

输入格式

输入文件的第一行为一个整数 n，表示节点的个数。

接下来 n−1 行，每行 2 个整数 a 和 b，表示节点 a 和节点 b 之间有一条边相连。

接下来一行 n 个整数，第 i 个整数 wi​ 表示节点 ii 的权值。

接下来 1 行，为一个整数 q，表示操作的总数。

接下来 q 行，每行一个操作，以 CHANGE u t 或者 QMAX u v 或者 QSUM u v 的形式给出。

输出格式

对于每个 QMAX 或者 QSUM 的操作，每行输出一个整数表示要求输出的结果。

输入输出样例

输入 #1复制

4
1 2
2 3
4 1
4 2 1 3
12
QMAX 3 4
QMAX 3 3
QMAX 3 2
QMAX 2 3
QSUM 3 4
QSUM 2 1
CHANGE 1 5
QMAX 3 4
CHANGE 3 6
QMAX 3 4
QMAX 2 4
QSUM 3 4

输出 #1复制

4
1
2
2
10
6
5
6
5
16

说明/提示

对于 100% 的数据，保证 1≤n≤3×104，0≤q≤2×105。

中途操作中保证每个节点的权值 w 在 −3×104 到 3×104 之间。

分析：

这里的sum和max性质不同，还是写两个函数来求解吧

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100005;
int n, m;
int w[N], h[N], e[N], ne[N << 1], idx;
int fa[N], son[N], sz[N], dep[N];
int id[N], nw[N], top[N], tot;
void add_edges(int a, int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int x, int father, int depth)
{
  dep[x] = depth, fa[x] = father, sz[x] = 1;
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == father) continue;
    dfs1(y, x, depth + 1);
    sz[x] += sz[y];
    if (sz[son[x]] < sz[y]) son[x] = y;
  }
}
void dfs2(int x, int t)
{
  id[x] = ++ tot, nw[tot] = w[x], top[x] = t;
  if (!son[x]) return;
  dfs2(son[x], t);
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == fa[x] || y == son[x]) continue;
    dfs2(y, y);
  }
}
struct Node{
  int l, r;
  ll mx, sum;
}tr[N << 2];
void pushup(Node &c, Node a, Node b)
{
  c.mx = max(a.mx, b.mx);
  c.sum = a.sum + b.sum;
}
void pushup(int u)
{
  pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r)
{
  if (l == r)
  {
    tr[u] = {l, l, nw[l], nw[l]};
    return;
  }
  tr[u] = {l, r};
  int mid = l + r >> 1;
  build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
  pushup(u);
}
void update(int u, int x, int c)
{
  if (tr[u].l == x && tr[u].r == x)
  {
    tr[u] = {x, x, c, c};
    return;
  }
  int mid = tr[u].l + tr[u].r >> 1;
  if (x <= mid) update(u << 1, x, c);
  else update(u << 1 | 1, x, c);
  pushup(u);
}
int qmax(int u, int l, int r)
{
  if (tr[u].l == l && tr[u].r == r) return tr[u].mx;
  int mx = -2e9;
  int mid = tr[u].l + tr[u].r >> 1;
  if (r <= mid) mx = max(mx, qmax(u << 1, l, r));
  else if (l > mid) mx = max(mx, qmax(u << 1 | 1, l, r));
  else
  {
    mx = max(mx, max(qmax(u << 1, l, mid), qmax(u << 1 | 1, mid + 1, r)));
  }
  return mx;
}
int qsum(int u, int l, int r)
{
  if (tr[u].l == l && tr[u].r == r) return tr[u].sum;
  int ans = 0;
  int mid = tr[u].l + tr[u].r >> 1;
  if (r <= mid) ans += qsum(u << 1, l, r);
  else if (l > mid) ans +=qsum(u << 1 | 1, l, r);
  else
  {
    ans += qsum(u << 1, l, mid) + qsum(u << 1 | 1, mid + 1, r);
  }
  return ans;
}
void update_path(int x, int c)
{
  update(1, id[x], c);
}
int Qmax(int u, int v)
{
  int mx = -2e9;
  while (top[u] != top[v])
  {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    mx = max(mx, qmax(1, id[top[u]], id[u]));
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) swap(u, v);
  mx = max(mx, qmax(1, id[v], id[u]));
  return mx;
}
int Qsum(int u, int v)
{
  int ans = 0;
  while (top[u] != top[v])
  {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    ans += qsum(1, id[top[u]], id[u]);
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) swap(u, v);
  ans += qsum(1, id[v], id[u]);
  return ans;
}
int main()
{
  memset(h, -1, sizeof h);
  cin >> n;
  for (int i = 1; i < n; i ++ )
  {
    int a, b; scanf("%d%d", &a, &b);
    add_edges(a, b);
    add_edges(b, a);
  }
  for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
  dfs1(1, -1, 1);
  dfs2(1, 1);
  build(1, 1, n);
  cin >> m;
  char op[20];
  while (m -- )
  {
    scanf("%s", op);
    if (!strcmp(op, "CHANGE"))
    {
      int x, c; scanf("%d%d", &x, &c);
      update_path(x, c);
    }
    else if (!strcmp(op, "QMAX"))
    {
      int u, v; scanf("%d%d", &u, &v);
      printf("%d
", Qmax(u, v));
    }
    else
    {
      int u, v; scanf("%d%d", &u, &v);
      printf("%d
", Qsum(u, v));
    }
    // cout << "----------" << endl;
  }
  return 0;
}

　　

P3178 [HAOI2015]树上操作

题目：

题目描述

有一棵点数为 N 的树，以点 1 为根，且树点有边权。然后有 M 个操作，分为三种：

• 操作 1 ：把某个节点 x 的点权增加 a 。
• 操作 2 ：把某个节点 x 为根的子树中所有点的点权都增加 a 。
• 操作 3 ：询问某个节点 x 到根的路径中所有点的点权和。

输入格式

第一行包含两个整数 N, M 。表示点数和操作数。
接下来一行 N 个整数，表示树中节点的初始权值。
接下来 N-1 行每行两个正整数 from, to ， 表示该树中存在一条边 (from, to) 。
再接下来 M 行，每行分别表示一次操作。其中第一个数表示该操作的种类（ 1-3 ） ，之后接这个操作的参数（ x 或者 x a ） 。

输出格式

对于每个询问操作，输出该询问的答案。答案之间用换行隔开。

输入输出样例

输入 #1复制

5 5
1 2 3 4 5
1 2
1 4
2 3
2 5
3 3
1 2 1
3 5
2 1 2
3 3

输出 #1复制

6
9
13

说明/提示

对于 100% 的数据， N,M<=100000 ，且所有输入数据的绝对值都不会超过 10^6 。

分析：

这题也很好写啊，真心不知道为啥全部改成long long就可以过，而部分为long long就WA

代码：

#include <bits/stdc++.h>
using namespace std;
// typedef long long ll;
#define int long long 
const int N = 100005;
int n, m;
int w[N], h[N], e[N << 1], ne[N << 1], idx;
int fa[N], son[N], sz[N], dep[N];
int id[N], nw[N], top[N], tot;
void add_edges(int a, int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int x, int father, int depth)
{
  dep[x] = depth, fa[x] = father, sz[x] = 1;
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == father) continue;
    dfs1(y, x, depth + 1);
    sz[x] += sz[y];
    if (sz[son[x]] < sz[y]) son[x] = y;
  }
}
void dfs2(int x, int t)
{
  id[x] = ++ tot, nw[tot] = w[x], top[x] = t;
  if (!son[x]) return;
  dfs2(son[x], t);
  for (int i = h[x]; ~i; i = ne[i])
  {
    int y = e[i];
    if (y == fa[x] || y == son[x]) continue;
    dfs2(y, y);
  }
}
struct Node{
  int l, r;
  int tag, sum;
}tr[N << 2];
void pushup(int u)
{
  tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
  Node &c = tr[u], &a = tr[u << 1], &b = tr[u << 1 | 1];
  if (c.tag)
  {
    a.sum += c.tag * (a.r - a.l + 1);
    b.sum += c.tag * (b.r - b.l + 1);
    a.tag += c.tag;
    b.tag += c.tag;
    c.tag = 0;
  }
}
void build(int u, int l, int r)
{
  if (l == r)
  {
    tr[u] = {l, l, 0, nw[l]};
    return;
  }
  tr[u] = {l, r};
  int mid = l + r >> 1;
  build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
  pushup(u);
}
void update(int u, int l, int r, int c)
{
  if (tr[u].l >= l && tr[u].r <= r)
  {
    tr[u].sum += (tr[u].r - tr[u].l + 1) * c;
    tr[u].tag += c;
    return;
  }
  pushdown(u);
  int mid = tr[u].l + tr[u].r >> 1;
  if (l <= mid) update(u << 1, l, r, c);
  if (r > mid) update(u << 1 | 1, l, r, c);
  pushup(u);
}
int query(int u, int l, int r)
{
  if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
  pushdown(u);
  int res = 0;
  int mid = tr[u].l + tr[u].r >> 1;
  if (l <= mid) res += query(u << 1, l, r);
  if (r > mid) res += query(u << 1 | 1, l, r);
  return res;
}
void update_path(int u, int c, int tag)
{
  if (tag == 2)
  {
    update(1, id[u], id[u] + sz[u] - 1, c);
  }
  else
  {
    update(1, id[u], id[u], c);
  }
}
int query_path(int u, int v)
{
  int ans = 0;
  while (top[u] != top[v])
  {
    // if (dep[top[u]] < dep[top[v]]) swap(u, v);
    ans += query(1, id[top[u]], id[u]);
    u = fa[top[u]];
  }
  // if (dep[u] < dep[v]) swap(u, v);
  ans += query(1, id[v], id[u]);
  return ans;
}
signed main()
{
  memset(h, -1, sizeof h);
  cin >> n >> m;
  for (int i = 1; i <= n; i ++ ) scanf("%lld", &w[i]);
  for (int i = 1; i < n; i ++ )
  {
    int a, b; scanf("%lld%lld", &a, &b);
    add_edges(a, b);
    add_edges(b, a);
  }
  dfs1(1, 1, 1);
  dfs2(1, 1);
  build(1, 1, n);
  while (m -- )
  {
    int p; scanf("%lld", &p);
    if (p == 1)
    {
      // printf("operation 1 :
");
      // for (int i = 1; i <= n * 2 - 1; i ++ ) cout << tr[i].sum << " "; cout << endl;
      int x, c; scanf("%lld%lld", &x, &c);
      update_path(x, c, 1);
      // for (int i = 1; i <= n * 2 - 1; i ++ ) cout << tr[i].sum << " "; cout << endl;
    }
    else if (p == 2)
    {
      // printf("operation 2 :
");
      // for (int i = 1; i <= n * 2 - 1; i ++ ) cout << tr[i].sum << " "; cout << endl;
      int x, c; scanf("%lld%lld", &x, &c);
      update_path(x, c, 2);
      // for (int i = 1; i <= n * 2 - 1; i ++ ) cout << tr[i].sum << " "; cout << endl;
    }
    else
    {
      int x; scanf("%lld", &x);
      printf("%lld
", query_path(x, 1));
    }
  }
  return 0;
}