首先题面是这样的:
给定一个正整数 k(3≤k≤15) ,把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列,例如,当 k=3 时,这个序列是:
1,3,4,9,10,12,13,…
因为所有的底数k都是相同的,所以自然要想到把他们的指数分离出来~~。
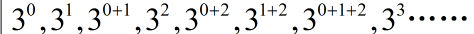 例如这样
例如这样
然后把指数分离出来:
0,1,0+1,2,0+2,1+2,0+1+2,3....
这时候看可能没什么头绪,但是再看一遍题目,你会发现题目中强调了两个字qwq——————— 递增。也就是说我们在确定第n项时,要从之前确定的n-1项中选出一项:
大于第n-1项但是小于目前能生成的任意一项,所以很容易想到:每确立一个数,就从数列的第一项开始逐个加上这一项,就造成了递增的效果。
但是这样做还有很大的缺陷,因为在前n-1项中,难免会有重复的项,举个最简单的例子:
0,1,0+1,2,0+2,1+2;
如果确立了第三项(0+1)的时候,对前面2项进行加法操作,明显会造成重复,并且不符合题目要求(递增和互不相等的方幂)。
那么这个算法就要进行改进。
在这里定义一下:
单独数:就是不是由加法操作得到的数(k的n次方那种qwq)
合成数:由单独数+合成数或由合成数+合成数组成的数
所以对于每一个合成数都有单独数的参与,我们想,可不可以先预处理出k的1-n次方,显然一个快速幂就可以了,那么再想想,如果每读入到一个单独数,就可以用这个单独数按照刚才的方式来得到后面的n-1项。
经过验证显然是可以的。
如样例:k=3,n=100时:
用f[i]代表第i项,有:
令v=每一个单独数f[i]
f[++i]=k(1 to n) v+f[k]
至此这个题目的分析就好了.....
下面是代码~
#include<bits/stdc++.h>
#define re register
#define ull unsigned long long
using namespace std;
int k,n,p;
ull a[1000],f[2000000];
inline int read() //读入优化
{
int k=1;
int sum=0;
char c=getchar();
for(;'0'>c || c>'9';c=getchar())
if(c == '-') k = -1;
for(; '0' <= c && c <= '9'; c = getchar())
sum = sum * 10 + c - '0';
return sum * k;
}
inline void out(int x) //输出优化
{
if(x < 0) { putchar('-'); x *= -1; }
if(x > 9) out(x / 10);
putchar(x % 10 + '0');
}
inline ull quick_pow(int r,int k) //快速幂
{
ull base=r,ans=1;
while(k!=0)
{
if(k&1) ans=ans*base;
base=base*base;
k/=2;
}
return ans;
}
int main()
{
//freopen("sequence.in","r",stdin);
//freopen("sequence.out","w",stdout);
k=read();n=read();
a[0]=1;a[1]=k;
for(re int i=2;i<=n;i++) a[i]=quick_pow(k,i); //预处理k的1-n(保险) 次幂
for(re int i=1;i<=n;i++)
{
f[i]=a[p];p++; //对于每一个单独数的赋值
ull tmp=f[i]; //记录v值(单独数)
int h=i; //确立i-1项(避免后来i的更新)
if(i>1)
{
for(re int j=1;j<h;j++)
{
f[++i]=tmp+f[j];
if(i>=n)
{
cout<<f[n]; //输出
return 0;
}
}
}
}
out(f[n]);
return 0;
}