Perface
- 莫队算法是一种用于处理一类支持离线的区间查询问题(基本上都和颜色有关)的
暴力算法。
- 它的主要思想是暴力查询,每次以尽量少的步数移动答案区间位置,从而达到一个可以接受的时间复杂度。
普通莫队
- 例题:给定一个长度为(N(Nin[1,10^5]))的数列,有(M(Min[1,10^5]))个询问,每次询问区间([a_i,b_i])中有多少种不同的数字。
- 考虑离线。我们可以把整个序列分为若干个大小为(k)块,预处理出每个点属于哪个块。将询问([a,b])以(a)所在块为第一关键字、(b)为第二关键字排序,每次算完当前询问答案则暴力跳到下一个询问的区间。
- 分析一下时间复杂度:对于左端点(l),它每次移动最多移(2k-1)步(从一个块的块首移到下一个块的块尾),而总共移(m)次;对于右端点(r),若(l)在一个块中,(r)最多移(n-1)步,而(l)总共可能在(frac nk)个块中。故为(O(mk+n^2k^{-1}))。
- 这是一个对勾函数,当(k=sqrt{frac{n^2}m}=nm^{-frac 12})时有最小值(O(nm^{frac 12}))。当然,在(n)、(m)相近时,也可近似取(k=n^{frac 12})。
- 这个的排序有个小优化:对于询问区间([a,b]),如果(a)在奇数块,按(b)升序排序;否则降序排序。这样就不会每次(l)进入新块时,(r)要从序列末尾跳回来。
struct query
{
int l,r,i;
inline bool operator<(const query a)const
{return bel[l]^bel[a.l]?bel[l]<bel[a.l]:bel[l]&1?r<a.r:r>a.r;}
}q[N];
带修莫队
- 例题:上面的例题加个操作——修改某个位置的数字,然后(n)、(m)范围降为(5*10^4)。
- 这看似不能离线了,也不好(CDQ)分治,但我们可以转换思路:记录操作的时间戳(t)。我们可以修改排序方式:将询问([a,b,t])以(a)所在块为第一关键字、(b)所在块为第二关键字、(t)为第三关键字排序。然后,同样是每次算完当前询问答案暴力跳到下一个询问的区间,同时计算在这段时间范围内的操作对该询问的影响。
- 那么结构体就改成这样:
struct query
{
int l,r,t,i;
inline bool operator<(const query a)const
{return bel[l]^bel[a.l]?bel[l]<bel[a.l]:bel[r]^bel[a.r]?bel[r]<bel[a.r]:bel[r]&1?t<a.t:t>a.t;}
}q[N];
尝试企图分析时间复杂度。左右两端点的移动步数不变;而对于时间端点(t),若(l)、(r)在一定的块中,(t)最多移最大时间(T)步。故为(O(mk+n^2k^{-1}+Tn^2k^{-2}))。- 这个怎么破?
我们对它求导:((mk+n^2k^{-1}+Tn^2k^{-2})'=m-n^2k^{-2}-2Tn^2k^{-3})。当它为(0)时,即为一个极值。假设(m)、(n)、(T)为同一数量级,我们给它乘一个(frac{k^3}n)变成(k^3-nk-2n^2=0)。那么直接套卡尔丹公式可得实根(k=sqrt[3]{n^2+sqrt{n^4-frac{n^3}{27}}}+sqrt[3]{n^2-sqrt{n^4-frac{n^3}{27}}})。是不是很妙?
- 我们可以大略地令(k=n^{frac 23}),那么时间复杂度即为(O(mn^{frac 23}))。这已经很优秀了,不必再苛求了。
(我不会告诉你我不会化简上面那个式子)
树上莫队
- 这是一个很
骚妙的东西。
- 先说一下欧拉序。我看别人的博客得知欧拉序大致有两种:第一种是括号序,即(dfs)时进/出某个点都将其入队;第二种,则是第一种+某个子节点结束时也将该点入队。这里采用第一种。
- 我们先求出树的欧拉序,记录每个点进/出时的时间戳(in_x)、(out_x)。对于一个询问((x,y)),记(z=lca(x,y)),若(x=z),则(x)到(y)的链对应欧拉序中的区间([in_x,in_y]);否则对应区间([out_x,int_y])。
- 这样会有一些点的左右括号都在里面,那些点是不在(x)到(y)的链中的,所以我们可以用一个类似异或的东西除去它们;还有,如果(x≠z),对应区间([out_x,int_y])中是没有(z)的,所以我们还要额外算(z)的贡献。
- 时间复杂度就同普通莫队了。
- 当然,这个也可以带修,当然是修改点权,复杂度同上。如果它敢修改树的形态,就可以考虑打
一个ETT之类的维护一下欧拉序暴力撵标算。
- 有一道例题:【GMOJ3360】【NOI2013模拟】苹果树,题意大概是:给定一颗大小为(N(Nin[1,50 000])的树,树的每个点有一种颜色;有(M(Min[1,10^5]))个询问,每次询问将颜色(a_i)视为颜色(b_i)的前提下(u_i)到(v_i)的链上的颜色种数。
Code
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
using namespace std;
const int N=21e4;
int i,j,n,m,col[N],x,y,tot,tov[N],nex[N],las[N],ti,ord[N],in[N],out[N],dep[N],anc[N][17],sz,bs,bel[N],now,s[N],cnt[N],ans[N];
struct query
{
int l,r,lca,a,b,i;
inline bool operator<(const query a)const
{return bel[l]^bel[a.l]?bel[l]<bel[a.l]:bel[l]&1?r<a.r:r>a.r;}
}q[N];
void read(int&x)
{
char c=getchar(); x=0;
for(;!isdigit(c);c=getchar());
for(;isdigit(c);c=getchar()) x=x*10+(c^48);
}
void dfs(int x)
{
ord[in[x]=++ti]=x;
for(int i=las[x],y;y=tov[i];i=nex[i])
if(y!=anc[x][0])
{
int j=1,f=anc[y][0]=x;
while(f) f=anc[y][j]=anc[f][j-1], j++;
dep[y]=dep[x]+1, dfs(y);
}
ord[out[x]=++ti]=x;
}
int LCA(int x,int y)
{
int i,fx,fy;
if(dep[x]<dep[y]) swap(x,y);
fd(i,15,0) if((fx=anc[x][i])&&dep[fx]>=dep[y]) x=fx;
fd(i,15,0) if((fx=anc[x][i])^(fy=anc[y][i])) x=fx, y=fy;
return x==y?x:anc[x][0];
}
inline void work(int p)
{
now+=s[p]*(~s[p]?!cnt[col[p]]++:!--cnt[col[p]]);
s[p]*=-1;
}
int main()
{
read(n), read(m);
fo(i,1,n) read(col[i]);
fo(i,1,n)
{
read(x), read(y);
if(!x|!y) continue;
tov[++tot]=y, nex[tot]=las[x], las[x]=tot;
tov[++tot]=x, nex[tot]=las[y], las[y]=tot;
}
dfs(1);
sz=round(ti/sqrt(m)), bs=ceil((double)ti/sz);
fo(i,1,bs) fo(j,(i-1)*sz+1,i*sz) bel[j]=i;
fo(i,1,m)
{
read(x), read(y), read(q[i].a), read(q[i].b);
if(in[x]>in[y]) swap(x,y);
int lca=LCA(x,y);
if(x==lca)
q[i].l=in[x], q[i].r=in[y];
else q[i].l=out[x], q[i].r=in[y], q[i].lca=lca;
q[i].i=i;
}
sort(q+1,q+m+1);
fo(i,1,ti) s[i]=1;
int l=1,r=0;
fo(i,1,m)
{
int ql=q[i].l, qr=q[i].r, lca=q[i].lca;
while(l<ql) work(ord[l++]);
while(l>ql) work(ord[--l]);
while(r<qr) work(ord[++r]);
while(r>qr) work(ord[r--]);
if(lca) work(lca);
ans[q[i].i]=now-(q[i].a^q[i].b&&cnt[q[i].a]&&cnt[q[i].b]);
if(lca) work(lca);
}
fo(i,1,m) printf("%d
",ans[i]);
}
回滚莫队(只增莫队)
- 这个是普通莫队的升级版,它支持求一些更为奇怪的东西。
- 比如有道例题: AT1219 [JOI2013]歴史の研究,这题加点容易删点难,而我们每次移动(l)、(r)指针又不得不删点。怎么破?
- 那么我们可以不删点。我们扫一遍每个块,先暴力处理左右端点在一个块的特殊询问(每个(O(k))),然后每次移右端点照样移(反正左端点同块右端点单增,只会加点),仍是(O(n^2k^{-1}));而左端点先以当前块尾+1为起点,先记录一波答案,左移左端点(这样也只会加点),然后下一波询问的时候将左端点变回起点并将答案变回来(当然,也要把左移左端点对桶的影响弄回来),于是这类似删点的操作复杂度也是(O(mk))。那么和普通莫队一眼,取(k=n^{frac 12})即可。
- 其他的以此类推吧。
与曼哈顿距离最小生成树有机结合♂♂
- 如果你觉得分块太玄,太容易T,那么我们可以考虑直接算出移动左/右端点的最小步数和方案。
- 具体地说,对于一个询问(i[a_i,b_i]),我们定义一个平面直角坐标系上的点(P_i(a_i,b_i)),那么询问(i)移到询问(j)的代价就是(P_i)和(P_j)的曼哈顿距离嘛。
- 那么就做最小生成树嘛,做出来之后按最小生成树的边走,绝对最优,撵爆分块。所以随便上个(Kruskal)或者(Prim)什么的就可以T了。等等,为什么会T?这是完全图啊!!!
- 但是,真正有用的边是远远小于(O(n^2))的。
- 有一个结论:以一个点为原点建立直角坐标系,在每45度内只会向距离该点最近的一个点连边。
- 这个分类讨论一下,随便证明。
- 这样一来,有用边数就是(O(n))级别的了。
- 考虑一个点(A(x0,y0))。它可以把平面分为8个部分:
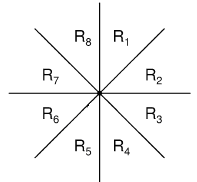
- 我们只需考虑在一块区域内的点,其他区域内的点可以通过坐标变换“移动”到这个区域内。为了方便处理,我们考虑图中的(R1)区域。在(R1)区域内的点(B(x1,y1))满足(x1≥x0∧y1-x1>y0-x0)。那么(|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0))。在(R1)的区域内距离(A)最近的点也即满足条件的点中(x+y)最小的点。因此我们可以将所有点按(x)坐标排序,再按(y-x)离散,用线段树或者树状数组维护大于当前点的(y-x)的最小的(x+y)对应的点。时间复杂度(O(Nlog_2N))。
- 至于坐标变换,一个比较好处理的方法是第一次直接做;第二次沿直线(y=x)翻转,即交换(x)和(y)坐标;第三次沿直线(x=0)翻转,即将(x)坐标取相反数;第四次再沿直线(y=x)翻转。注意只需要做4次,因为边是双向的。
- 求出所有有用边后,我们再做一波(Kruskal),即可在(O(Nlog_2N))的复杂度内快乐解决。