codeforces 1244D Paint the Tree 题解

updated 2019.11.10 之前笔误了

首先这题的条件就在于 一棵树上任意两个距离(leq2)的点颜色不同 并且只有三种颜色

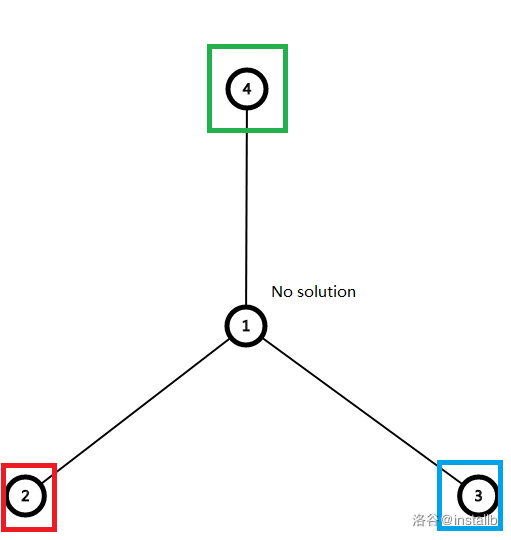
那么如果存一个点(u) 有三个点与(u)相连 这三个点颜色就必须两两不同
然后这三个点就把三种颜色取完了
然后(u)就没办法取颜色了 这样就无解

于是 只要存在任意一个节点的度数(geq3)就无解

然后我们发现这棵树是条链

再看这个链 任意三个相连的节点都需要两两颜色不同
所以任意三个相连的节点只要确定了两个 第三个就确定了 就可以一步一步推下去了
一开始就随便找一条边 与这条边相连的两个点分别枚举选什么颜色(这两个点颜色不能相同) 然后一步一步往外推 记录下六种情况下答案最小的情况 就可以了

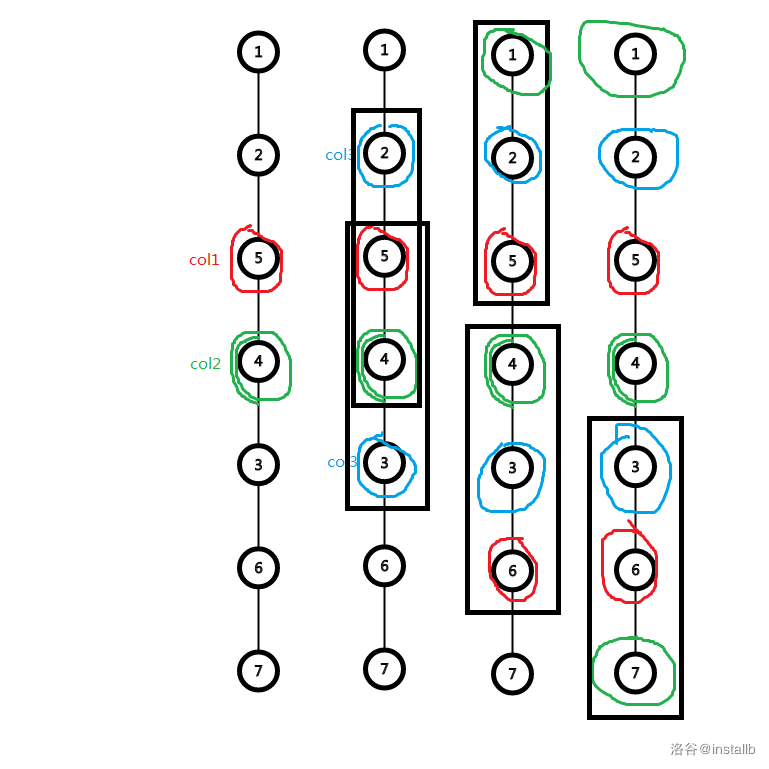
放个图吧 好理解

确定过程(枚举(col1)和(col2) 这里随便找一条边都行 我找了((4,5))这条边)

下面是无解情况

记录下每个点在这种情况下(枚举6种情况)标记成什么颜色 然后直接全部加起来 统计答案

这是考场代码 我都是直接dfs的 其实不用 但反正复杂度对的 无所谓

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
using namespace std;
typedef long long LL;
 
LL n,m,k;
LL c[4][800005] = {0};
LL ans = 0;
string s;
 
LL ec = 0,to[800005],nxt[800005],hed[200005] = {0};
LL deg[400005] = {0};
void add_edge(LL f,LL t){
	++ ec; to[ec] = t; nxt[ec] = hed[f]; hed[f] = ec;
	deg[t] ++;
}
 
LL col[200005] = {0};
LL rec[200005] = {0};
 
LL chg(LL x,LL y){
	return 6 - x - y; // 小技巧 根据另外两点颜色确定该点颜色
}
 
void dfs(LL u,LL f,LL uc,LL fc){ // 标记颜色
	for(LL i = hed[u];i;i = nxt[i]){
		LL v = to[i];
		if(v == f) continue;
		col[v] = chg(uc,fc);
		dfs(v,u,col[v],uc);
	}
}
 
int main(){
	LL a,b;
	ios::sync_with_stdio(false);
	cin >> n;
	for(LL i = 1;i <= n;i ++) cin >> c[1][i];
	for(LL i = 1;i <= n;i ++) cin >> c[2][i];
	for(LL i = 1;i <= n;i ++) cin >> c[3][i];
	
	for(LL i = 1;i < n;i ++){
		cin >> a >> b;
		add_edge(a,b);
		add_edge(b,a);
	}
	
	for(LL i = 1;i <= n;i ++){
		if(deg[i] >= 3){
			cout << -1 << endl;
			return 0;
		}
	}
	LL ans = 0x3f3f3f3f3f3f3f3f;
	for(LL c1 = 1;c1 <= 3;c1 ++){
		for(LL c2 = 1;c2 <= 3;c2 ++){
			if(c1 == c2) continue;
			col[a] = c1; col[b] = c2; // 随便找一条边 枚举
         // 我在这里直接用了最后输入的那条边
			dfs(a,b,c1,c2);
			dfs(b,a,c2,c1);
        // 注意要从两个点两个方向 都要dfs 
			LL cnt = 0;
			for(LL i = 1;i <= n;i ++) cnt += c[col[i]][i];
			if(cnt < ans){
				ans = cnt;
				for(LL i = 1;i <= n;i ++) rec[i] = col[i]; // 记录答案
			}
		}
	}
	cout << ans << endl;
	for(LL i = 1;i <= n;i ++) cout << rec[i] << (i == n ? '
' : ' '); 
	return 0;
}

顺带一提 这场CF的D比C还简单