0-1背包之C语言
01背包问题应该算是一个很经典的问题了,接下来实现一下
问题:
现给出一个容量为V的背包和N件物品,每件物品的体积为v[i],价值为c[i],将几件物品装入背包内,使得物品总体积不超过背包体积,并且使总价值最大,求这个最大值?
给出一组数据:
V = 8,N = 4;
i 1 2 3 4
v 2 3 4 5
c 3 4 5 6
解题思路:
用 f[i][j] 表示前 i 种物品,背包容量为 j 时的最大价值
首先初始化数组 f[][]
当 i=1 时,如果背包可以放下第一个物品,则放入,更新最大价值
基于第一行的结果和背包容量,可以选择选或者不选第二件,取最大价值
…
不断更新,直到最后一个值的时候就知道最大价值了
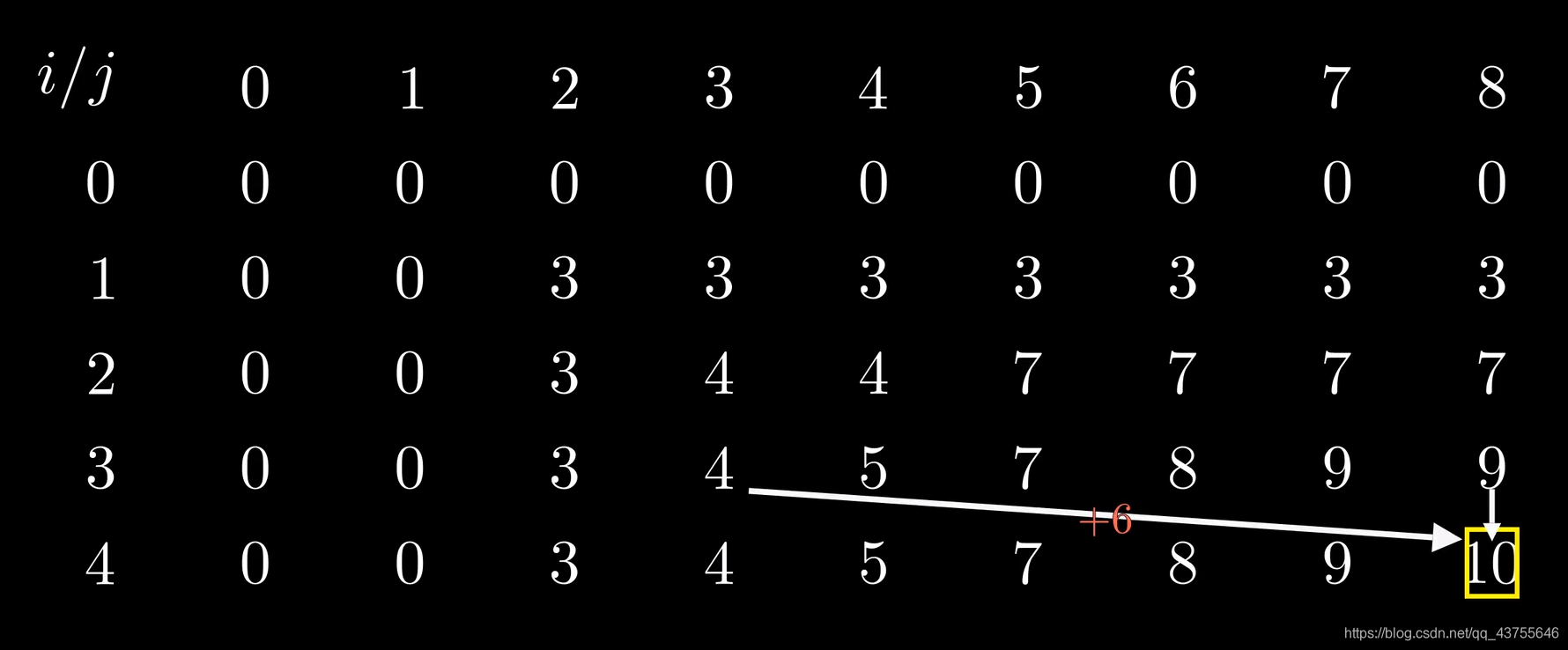
看下面的图:
f[i][j] 表示前 i 种物品,背包容量为 j 时的最大价值
这样就可以明显的看出来了
状态转移方程
f[i][j] = max(f[i-1][j],f[i-1][j-v[i]] + c[i])
代码部分
#include <stdio.h> #include <stdlib.h> #define maxn 10 #define maxv 10int max(int a,int b)
{
if(a>b){
return a;
}
else{
return b;
}
}int main()
{
int N,V,f[maxn][maxv],c[maxn],v[maxn];
printf("请输入背包总量和物品数量: ");
scanf("%d %d",&V,&N);
printf("请依次输入物品体积和价格: ");
for(int i=1;i <= N;++i)
scanf("%d %d",&v[i],&c[i]);
for(int i=1;i <= N;++i)
for(int j=1;j <= V;++j){
f[i][j] = f[i-1][j];
if(j >= v[i])
f[i][j] = max(f[i-1][j],f[i-1][j-v[i]] + c[i]);
}
printf("最大价值:%d ",f[N][V]);
return 0;
}
附件一个讲的不错的视频演示:
01背包视频演示