Tarjan算法初步

一、前置知识：
　　　强连通分量：有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大（看清是极大，不是最大）强连通子图，称为强连通分量(strongly connected components)。一个点x，若没有点与它强连通，则它自己也是一个强连通分量。

二、算法简述

　　　Tarjan算法是一个主要用于求有向图的强连通分量或无向图的环的算法。（当然也有很多扩展，与其他一些神奇的算法搭配可能会碰撞出奇妙的火花）

　　　（无向图的极大连通子图就不叫强连通分量了，叫连通分量。实际上求无向图的连通分量用bfs就行了（毕竟无向图没有方向，只要能到达，就是连通，也没有强连通这一说））

三、原理：　

　　　想象一个情景：从一个点u出发，一直向下遍历，然后忽得找到一个点，那个点x竟然有条指回点u的边！

　　　那么想必这个点u能够从自身出发再回到自身

　　　想必这个点u和其他向下遍历的该路径上的所有点构成了一个环，

　　　想必这个环上的所有点都是强联通的。

 

　　　但只是强联通啊，我们需要求的可是强连通分量啊......怎么在退回到这个点的时候，知道所有和这个点u构成强连通分量的点呢？

　　　开个栈记录就行了。我们建一个栈，保证回溯到u时栈中u及u上面的点组成一个强连通分量，然后把它们弹出、记录就好了。

　　　似乎做法已经明了了，用程序应该怎么实现呢？

四、程序实现：

　　　　首先需要介绍一些辅助数组

(1)、dfn[ ]，表示这个点在dfs时是第几个被搜到的。
(2)、low[ ]，表示这个点以及其子孙节点连的这个点及其祖先中dfn最小的值
(3)、stack[ ]，表示当前所有可能能构成强连通分量的点。
(4)、vis[ ]，表示一个点是否在stack[ ]数组中。

　　　　那么按照之上的思路，我们来考虑这几个数组的用处以及算法的具体过程。

　　　　假设现在开始遍历点u：

1. 首先初始化dfn[u]=low[u]=第几个被dfs到
   dfn可以理解，但为什么low也要这么做呢？
   因为low的定义如上，也就是说如果没有子孙与u的祖先相连的话，dfn[u]一定是它和它的所有子孙中dfn最小的（因为它的所有子孙一定比他后搜到）。

2. 将u存入stack[ ]中，并将vis[u]设为true
   stack[ ]有什么用？
   如果u在stack中，u之后的所有点在u被回溯到时u和栈中所有在它之后的点都构成强连通分量。(也就是上文中所说的开个栈记录)

3. 遍历u的每一个能到的点，如果这个点dfn[ ]为0，即仍未访问过，那么就对点v进行dfs，然后low[u]=min{low[u],low[v]}        
   low[ ]有什么用？        应该能看出来吧，就是记录一个点它最大能连通到哪个祖先节点（当然包括自己）
   如果从u遍历这个点之前这个点就被遍历到了，那么看它当前有没有在stack[ ]里，如果有（要么这个点是u的祖先，要么这个点与u的某个祖先强连通，反正这个点能到达u），说明这个点肯定能到达u，同样u能到达他，他俩强联通，那么low[u]=min{low[u],low[v]}
   如果已经被弹掉了，说明无论如何这个点也不能与u构成强连通分量，因为它不能到达u（当处理强连通分量时才将元素弹出栈。处理包含这个点的强连通分量时没有处理掉u，就说明u不在它的强连通分量里）

4. 假设我们已经dfs完了u的所有的子树，那么之后无论我们再怎么dfs，u点的low值已经不会再变了。 
   那么如果dfn[u]=low[u]这说明了什么呢？
   再结合一下dfn和low的定义来看看吧
   dfn表示u点被dfs到的时间，low表示u和u所有的子树所能到达的u的祖先中dfn最小的。
   这说明了u点及u点之下的所有子节点没有边是指向u的祖先的了，即我们之前说的u点与它的还在栈中的子孙节点构成了一个最大的强连通图即强连通分量
   此时我们得到了一个强连通分量，把所有的u点以后压入栈中的点和u点一并弹出，将它们的vis[ ]置为false，如有需要也可以给它们染上相同颜色（后面会用到，用于缩点等等）

　　　　　　代码大概长成这样

　　　　　　

 　　

　　　　　　对了，tarjan一遍不能搜完所有的点，因为存在孤立点或者其他

　　　　　　所以我们要对一趟跑下来还没有被访问到的点继续跑tarjan

　　　　　　怎么知道这个点有没有被访问呢？

　　　　　　看看它的dfn是否为0！

　　　　　　

　　　　

　　　　　　非常简短的tarjan复杂度证明：

　　　　　　　　思考每个点最多被dfs一次，所以均摊下来复杂度是O(n)的

　　　　　　　　证毕

五、扩展：

　　tarjan缩点：

　　　　1.什么时候要用缩点

　　　　众所周知，有向无环图总是有着一些蜜汁优越性，因为没有环，你可以放心的在上面跑dfs，搞DP，但如果是一张有向有环图，事情就会变得尴尬起来了

　　　　思考一下会发现如果不打vis标记就会t飞（一直在环里绕啊绕），但是如果打了，又不一定能保证最优解

　　　　而你一看题目却发现显然根据一些贪心的原则，这个环上每个点的最大贡献都是整个环的总贡献

　　　　这个时候缩点就显得很有必要了，因为单个点的贡献和整个环相同，为什么不去把整个环缩成一个超级点呢？

　　　　这个环只是为了好理解，事实上他应该是一个强连通分量，显然如果只缩掉一个强连通图，图中仍然有环存在

　　　　缩点的一个栗子

　　　　 -----------> 

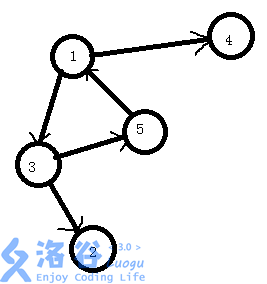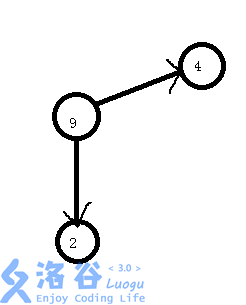
　　　　2.怎么缩点

　　　　还记得之前tarjan里的染色吗？

　　　　我们只需要把同一颜色的点权加到一块，然后把该颜色指向不同颜色的边建好就可以了

　　　　代码就不贴了，因为不同的题有不同的处理方法

　　无向图tarjan求环：

　　　　每次tarjan递归时记录父亲节点到儿子节点走的边的对应相反边（因为无向图对于一条边用前向星存的话要插入2次），若儿子在不走这条边的情况下仍能得到小于dfn的low，即可走另一条路径到达父亲节点的祖先，说明有一个环。并且若干个相交的环会以一个强连通分量的形式呈现出来。

　　无向图tarjan求割点：www.cnblogs.com/collectionne/p/6847240.html

　　　　　　该博客有一处low的维护操作与普通tarjan不同：low[u] = min(low[u], dfn[v]);

　　　　　　这里解释一下：若v已经被遍历过了，这时遍历到u发现u与v有连边。这说明什么？v还没有被回溯。因为这时无向图，既然u能到v，那v也能到u，当回溯到v时，v所能到的点必然都已经被遍历完了。这里刚遍历到u，不就说明v还没有被回溯到嘛。这样，v不就是u的祖先了嘛。

大量摘自洛谷博客：初探tarjan算法（求强连通分量），略有修改。在此对作者：Styx  表示真挚的感谢。