原文传送:https://www.luogu.com.cn/blog/1239004072Angel/post-shuo-xue-qiu-xie-yi-lei-fang-cheng-di-fang-fa
不推荐只看原文进行学习。
裴蜀定理 (ax+by的最小正值还能整除a,b, 该最小正值为gcd(a,b))。
方程ax+by=c (a,b,c为整数)有整数解的充要条件为gcd(a,b) | c 原博客只证明了充分性,这里证明必要性:
若方程有整数解x1,y1,则c=ax1+by1。因为ax1+by1能被 gcd(a,b)整除,则c必然能被gcd(a,b)整除,否则方程无解。(一个方程变形罢了)
扩展欧几里得算法:
总的来说,扩展欧几里得用来求不定方程ax+by=c的整数解或线性同余方程ax≡c mod b。利用欧几里得算法框架递归到b=0后返回得到答案。
推到a′x+b′y=b′x'+(a′modb′)y' ① 时(注意等号两边的a'是同一个数(b'同理),但x和x'不是同一个数(y和y'同理),原博客没有体现出来),可令a''=b',b''=a′modb′,那么方程能像这样再一直等于下去,直到 某个b'...' (这里省略号是若干'的意思)为0 (a,b的变化就是欧几里得算法的过程),那么此时方程为a'...' x = gcd(a'...',0)=a'...',得到x'...'=1,y'...'=任意整数 的解。为了方便,可以取y'...'=0。加上 下文已知, 后面的方程的解可推出前面方程的解,那么一开始的方程就解出来了。
一个更清楚的口胡解释:方程a′x+b′y=gcd(a',b')和b′x'+(a′modb′)y'=gcd(b′,a′modb′) 都有解(裴蜀定理)(也许用表示联立的大括号表示更直白),同时 gcd(a',b')=gcd(b′,a′modb′) 。解出方程b′x'+(a′modb′)y'=gcd(b′,a′modb′) 后,方程a′x+b′y=gcd(a',b')=gcd(b′,a′modb′)=b′x'+(a′modb′)y' (此时x' 、y‘ 确定,b′x'+(a′modb′)y'为一个定值),这时方程最右边可变形为:a′y’+b′(x‘−b′/a′ * y’),即a′x+b′y=a′y’+b′(x‘−b′/a′ * y’),这里面a',b',x',y'都已知,那么取x=y',y=x‘− b′/a′ * y’就是原方程的一个解。这时可以知道,要求当前不定方程ax+by=gcd(a,b)的解,可看它对应的下一个方程bx'+(a%b)y'=gcd(b,a%b)的解,而这”下一个方程“的解,又可以看它的下一个方程即“下下个方程‘’…直到最后看的方程的第二个系数为零,得解,再按顺序返回到第一个方程,就得到了答案。(递归的依据就是gcd(a,b)=gcd(b,a%b),故叫扩展欧几里得,还能顺便求出最大公因数)
对于方程ax+by=c (gcd(a,b)|c) 设k=c/gcd(a,b) 求出ax+by=gcd(a,b)的解x,y后将x,y都*k 即为ax+by=c 的一组特解。
代码:
1 int exgcd(int a,int b,int &x,int &y) 2 //调用函数完成后传址&x,&y的变量的值就为关于当前函数a,b的值的ax+by=gcd(a,b)的解(x,y) 3 { 4 if(!b) 5 { 6 x=1;y=0; 7 return a; 8 } 9 int g=exgcd(b,a%b,y,x);//反着传址,省去后文交换x,y的值 10 y-=a/b*x; 11 return g; 12 } 13 14 int main()//求解不定方程ax+by=c 15 { 16 int a=read(),b=read(),c=read(),x,y; 17 int g=exgcd(a,b,x,y),e=c%g;//按址传递形参。 18 //不写按址传递形参的话,可以写结构体或全局变量 19 if(e)//无解 20 { 21 cout<<"NONE"; 22 return 0; 23 } 24 x*=c/g;y*=c/g;//不要忘了c不一定是gcd(a,b) 25 cout<<x<<endl<<y; 26 return 0; 27 }
上面讨论的情况只是a,b,c都大于0的情况。当a,b,c有小于0的情况时,特判一下:若是a或b小于0,则完全可以把负号去掉,最后再给x或y变下号就好;若是c小于0,那么c/g小于0,并不需要做什么多余操作;若a,b小于0,可等号两边都提出一个-1来,转化成c小于0的情况;若a,b,c都小于0,则可等号两边都提出一个-1来,转化成a,b,c大于0都情况。第一种情况相当于换元,故x或y最后要额外处理,后两种情况是方程的变形,不会改变解。
也可以不用这么麻烦。若会小于0,算法向下递归的正确性不变,只是递归到b=0时,a可能为负值,此时2种处理:
1、算法返回a的绝对值,满足exgcd返回值仍为gcd(a,b),令x= a<0 ?-1 :1 (因为gcd一定是非负的)
2、令x=1,算法返回a,exgcd返回值(设为g)的绝对值才是gcd,且此时x,y是满足ax+by=g的一组解(ax+by=-gcd一样有解,那么也可凭此递归下去,因为能递归下一层的依据就是构造了两个等号右边一样(不管是gcd还是-gcd),左边系数有关系、可变形为同样形式的方程,这样求出一个方程的解,另一个就可根据形式写出解)。
求出不定方程ax+by=c (a,b>0)的一组特解x0,y0后,他的所有解都可以表示为:x=x0+k*(b/gcd(a,b)),y=y0-k*(a/gcd(a,b)),k为整数。对于a,b有小于0的情况,根据上文来转化为a,b大于0的情况,最后决定是否对x,y变号。
简单证明:不定方程ax+by=c (a,b>0)的解相对于x0,y0都可以表示成x=x0+u,y=y0+v的形式,且u和v异号(因为a,b>0)。设d=a,b的最小公倍数,则d=a*b / gcd(a,b) 。
考虑x0缓慢增加(减少同理)以找到新的解,发现只有ax增加的量w为d的倍数时,by才能没有在b、y都为整数的情况下抵消ax的增加量(w一定为a的倍数,否则x不为整数,w若不为b的倍数,则y不为整数。故若要求解为整数(不定方程的要求),w必为a,b的公倍数,即为d的倍数,w=kd,同时也说明相对于x0,y0的ax的变化量不为a,b的公倍数的解x,y是不存在的)ax变化了kd(增加还是减少要看k的符号)=k* a*b / gcd(a,b),则x变化了k* b/gcd(a,b),by要向反方向变化kd ,得y变化了 -k * a/gcd(a,b) 。得证x=x0+k*(b/gcd(a,b)),y=y0-k*(a/gcd(a,b))一定还是原方程的解
时间复杂度:与欧几里得算法同级,上限都为logn,随机数据下会更快。
简单证明:考虑a,b,a%b,b%(a%b)。a%b一定<b,猜想复杂度logn的话,考虑b%(a%b)与b/2的大小关系,而这又与a%b有关(因为b%(a%b) < a%b)。因为关键节点就是b/2,想到分两种情况:
a%b> b/2,则b%(a%b)=b- a%b < b/2;
a%b< b/2,则b%(a%b)<a%b< b/2;
发现gcd或exgcd函数每递归两层,函数的第二参数的规模就减少至少一半,故复杂度上限级别为log b。
例题:洛谷P2421 [NOI2002] 荒岛野人 https://www.luogu.com.cn/problem/P2421
注意当ax+by=c的(a,b)=1时,通解x=x0+k*b的形式才成立,否则(a,b)不一定为1时通解应为标准形式x=x0+k*b/gcd(a,b),不要忘了一般情况下的通解公式的后部是有除以gcd的(要找全解,ax就要不断变化a,b最小公倍数的量(a,b才是常数),x就变化b/gcd(a,b)的量)。y同理。
还是容易在做完exgcd后忘记给解乘c/gcd(a,b),别忘了做完exgcd求出的是方程ax+by=gcd(a,b)的解,是不是ax+by=c的解还要再详看(有可能还无解呢)。
所谓的“想当然”最好自证一下再用。相似的概念并行思考时容易混淆,注意区分。
注意:若想防止溢出,exgcd中不能简单地对x,y模b/d,a/d。通解公式中x,y一个变化了,另一个也会变化。
上文‘%’号未经特殊说明的话都指取余运算(毕竟我的语言环境是c++)。
中国剩余定理CRT(本文该模块中bi是同余号右边的数,ai是模数,ti是mi在模ai下的逆元):
总的来说,用于求解模数互质系数为1的线性同余方程组。利用各模数与相应逆元构造了一个某模数下对应项结果为bi,其他项全是0的可行解。
原文的“数学归纳”原来也是假设最后的解有多个再相减证明公倍数整除差值。
证明及详解(更清楚明确,还有个明确的性质):孙子定理 https://baike.baidu.com/item/%E5%AD%99%E5%AD%90%E5%AE%9A%E7%90%86/2841597?fromtitle=%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86&fromid=11200132&fr=aladdin
对于: 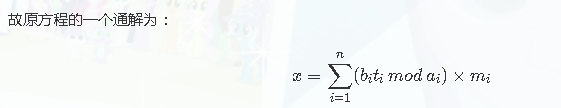
能在biti处模ai的原因:不管怎样,mi必须要是除了自己(ai)的其他所有模数的乘积,以保证在被其他模数取模时结果为0,只剩下那个模数对应的项,才能保证正确性。而biti在模ai时才会看到,在最后答案中模ai的话,不会影响正确性,同时减少数值范围(但不能对mi取模)
代码很简朴,先求出模数积(O(n)),依次求出所有mi (O(n)),ti (O(nlogn)),最后求出答案。总时间复杂度:O(nlogn)
若方程组其中的同余方程的x前有系数,可用扩展欧几里得解出该方程,转化为系数为1的形式,最后总时间复杂度不变。
扩展中国剩余定理(模数不一定两两互质时求解同余方程组):
用于求解模数不一定互质的线性同余方程组。通过联立逐步合并方程组至一个方程。
为方便理解中国剩余定理,有一个引理:对于两个互质的正整数模数 n, m,给出两个整数 a,b满足 0≤a<n,0≤b<m,则在[0,nm)中存在且仅存在一个 同余方程组{ x modn =a,x mod m=b }的解 。
证明很容易理解,n,m互质时同余方程组一定有多个解(由中国剩余定理百度百科可知)。对于同余方程组的两个解x1,x2。作差得y ,y可同时被n 、m整除,即y为n,m的公倍数,那么在x1,x2他们的差距一定是n,m最小公倍数的倍数,x1,x2不相等的情况下最少也差lcm(n,m)(n,m互质的情况下lcm(n,m)即为nm),此时引理结论可得证。
若模数不一定互质(对应扩展中国剩余定理),在方程组有解时(有解的条件下文再讨论),也是会有多个解,对于这时的解 x1,x2,差y可同时被n 、m整除,仍为n,m的公倍数,x1,x2不相等的情况下最小差距还是n,m的最小公倍数。最后可知模数不一定互质时,若有解,则[0,lcm(n,m))中只会存在一个解 。
由于 ai 之间可能不互质,故我们可能找不到某个 mi 在模 ai 意义下的逆元,就无法用CRT的公式求解。
算法核心:变形等式,合并方程:

两个方程组是等价的,对第二个方程组找条件性质/变形 求解,即为原方程组的解。
又等价于: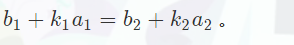

方程通解可由上文引理印证,也知lcm是通解的最小变化量。其实上图第一行变形的等号右边应该是b2-b1,代码中写的也是b2-b1。exgcd中的参数可以直接传a1和a2(不用传-a2),这样得到的k1,k2乘上(b2-b1)/exgcd 后,k1是正确值,k2是正确值的相反数,但要求出x,只需求出k1和k2中的一个正确值就好。
故对于 n 个方程,我们顺次合并两个方程即可。在合并过程中发现一处无解,那么方程组就无解。
时间复杂度:nlogn
启发思路:
对于有很多个方程的方程组,可以划分部分,在各个部分里求出满足当前部分的所有方程的解,最后再求同时满足各部分的解的解,即为总方程组的解(分治再合并);
以后在整数意义下有两个未知数的方程都可解了。
杂想:扩展CRT会取代中国剩余定理吗?在OI中,扩展CRT更泛用,运算时的数值范围大头在求lcm上,比普通CRT不需要实现判断模数两两互质、更不易溢出数据类型。但要明白,能逐个合并方程的前提是我们用计算机写代码,让计算机做这些重复的活,而中国剩余定理直接给出一个最后答案的表达式,适合人工计算,这也是日常中现阶段数学和信息的一个区别吧。
例题:P4777 【模板】扩展中国剩余定理(EXCRT)https://www.luogu.com.cn/problem/P4777
AC代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 6 #define ll long long 7 #define ull unsigned long long 8 #define min(a,b) ((a)>(b)?(b):(a)) 9 #define max(a,b) ((a)>(b)>(a):(b)) 10 #define swap(a,b) ((a)^=(b),(b)^=(a),(a)^=(b)) 11 12 using namespace std; 13 14 const int N=1e5+5; 15 16 ll n,ai[N],bi[N],a1,b1,m,k1,k2; 17 18 inline ll read()//int N+ 19 { 20 ll x=0; 21 char ch=getchar(); 22 while(!isdigit(ch)) ch=getchar(); 23 while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar(); 24 return x; 25 } 26 27 ll exgcd(ll a,ll b,ll &x,ll &y) 28 { 29 if(!b) 30 { 31 x=1;y=0;//此题a,b都非负 32 return a; 33 } 34 ll d=exgcd(b,a%b,y,x); 35 y-=a/b*x; 36 return d; 37 } 38 39 inline ll mul(ll a,ll b,ll mod)//快速乘,防溢出 40 { 41 ll ret=0; 42 bool f=0; 43 if(b<0) 44 { 45 f=1; 46 b=-b; 47 } 48 while(b) 49 { 50 if(b&1) 51 ret=(ret+a)%mod; 52 b>>=1; 53 a=(a+a)%mod; 54 } 55 return f?-ret:ret; 56 } 57 58 int main() 59 { 60 n=read(); 61 for(int i=1;i<=n;++i) 62 ai[i]=read(),bi[i]=read(); 63 m=a1=ai[1],b1=bi[1]; 64 ll c,d; 65 for(int i=2;i<=n;++i)//EXCRT算法核心过程 66 { 67 c=bi[i]-b1; 68 d=exgcd(a1,ai[i],k1,k2); 69 m*=ai[i]/d; 70 b1=(mul(mul(k1,c/d,m),a1,m)+b1)%m;//(k1*(c/d)*a1+b1)%m 71 a1=m; 72 } 73 if(b1<0) 74 b1+=m;//答案要>=0 75 printf("%lld",b1); 76 return 0; 77 }
思路很简单,对溢出的处理废了点思考时间。说实话该代码没有对exgcd中做防溢出处理,luogu的数据还是弱了。除了高精度(极限情况下数值范围是个2*18*log2 1018 =2176位数,)有正确性更优的算法:https://www.luogu.com.cn/blog/user31435/solution-p4777
思考过程想到的性质:
lcm(a,b) >=lcm(b,a%b) 当a<b时等号成立
若想防止溢出,exgcd中不能简单地对x,y模b/d,a/d。通解公式中x,y一个变化了,另一个也会变化。
杂项:
两算法都不要忘判断无解的情况。扩展欧几里得初步求出的解的是ax+by=gcd(a,b)的解,不代表ax+by=c一定有解。
做数据范围很大的乘法时可能要注意模不同数时不同的应用环境,例如在CRT解的公式的最终结果是对M取模,除了前文提到的,计算时不能随便对某个模数处处取模。很多式子后面没有注明“模的意义下”,不要一看到大数计算就想当然要取模,会碍到/误导 思考分析。
为什么在取模意义下的乘法式子中无论以任意顺序取模,结果都是正确且唯一的:设模数为m,一个数/式子的结果都能分解成km+r的形式,由分配律拆开后,km的那部分无论乘什么,结果在模意义下都是0,那么原式的结果就等于给那个数/式子取模后的新式子的结果。
同余与等式常常转换。