皇后问题（BFS解法）

Description

在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。

Input

输入的第一个为测试样例的个数T，接下来有T个测试样例。每个测试样例的只有一行一个数n （ n < 15 ），表示棋盘的大小。

Output

对应每个测试样例输出一行结果：可行方案数。

Sample Input

2 3 4

Sample Output

0 2

 

记录一下用BFS来解皇后问题

DFS解法跳转

问题分析：

不同于DFS，BFS主要是用队列来实现，遍历行，在当前棋盘状态下将下一行所有可能性入队。

这就需要在每一个节点存储当前棋盘状态

无优化代码

#include<iostream>
#include<queue>
using namespace std;
#define MAX_DATA 15
struct point
{
    int x;
    int y;
    int m[MAX_DATA][MAX_DATA];
    int length;
};
int n;
queue<point> q;
int ans;
void init(point& p)
{
    for(int i=0;i<n;++i){
        for(int j=0;j<n;++j){
            p.m[i][j]=0;
        }
    }
}
void doFlag(point& p)
{
    for(int i=0;i<n;++i){
        p.m[p.x][i]=1;
        p.m[i][p.y]=1;
    }
    int i=1,x1=p.x,y1=p.y;
    while(x1-i>=0||y1-i>=0||x1+i<n||y1+i<n){
        if (x1-i>=0&&y1-i>=0){
            p.m[x1-i][y1-i]=1;
        }
        if (x1-i>=0&&y1+i<n){
            p.m[x1-i][y1+i]=1;
        }
        if (x1+i<n&&y1-i>=0){
            p.m[x1+i][y1-i]=1;
        }
        if (x1+i<n&&y1+i<n){
            p.m[x1+i][y1+i]=1;
        }
        i++;
    }
}
void bfs()
{
    for(int i=0;i<n;++i){
        point p;
        p.x=0;
        p.y=i;
        p.length=1;
        init(p);
        doFlag(p);
        q.push(p);
    }
    while(q.size()){
        point fp=q.front();
        int len=fp.length;
        if(len==n){
            ans++;
        }
        q.pop();
        for(int i=0;i<n&&len!=n;++i){
            if(!fp.m[len][i]){
                point p=fp;
                p.x++;
                p.y=i;
                p.length++;
                doFlag(p);
                q.push(p);
            }
        }
    }
}
int main()
{
    int T;
    cin>>T;
    while(T--){
        cin>>n;
        ans=0;
        bfs();
        cout<<ans<<endl;
    }
    return 0;
}

但是这样子实现太费空间了

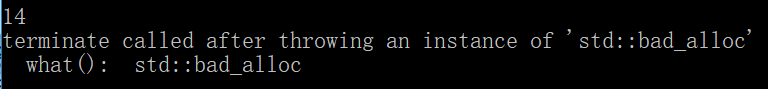
 当n==14时，会报错提示已占用内存过大

 queue的大小时比较难简化了，就简化节点试试

 第一步优化代码

#include<iostream>
#include<queue>
using namespace std;
#define MAX_DATA 15
struct point
{
    int m[MAX_DATA];///m[i]表示第i行m[i]有皇后
    int length;
};
queue<point>que;
int n;
int ans;
bool ok(point nowsta,int len)
{
    for(int i=1;i<len;i++){
        if(abs(nowsta.m[len]-nowsta.m[i])==abs(i-len)|| nowsta.m[len] == nowsta.m[i])
            return false;
    }
    return true;
}
void bfs()
{
    for(int i=1;i<=n;i++){///初始n个点加进去
        point p;
        for(int j=1;j<=n;j++) p.m[j]=0;
        p.m[1]=i;
        p.length=2;
        que.push(p);
    }
    while(!que.empty()){
        point p=que.front(); que.pop();
        if(p.length>n){
            ans++;
            continue;
        }
        int nowrow=p.length;
        p.length++;
        for(int i=1;i<=n;i++){///枚举列
            p.m[nowrow]=i;
            if(ok(p,p.length-1)) que.push(p);
        }
    }
}
int main(){
    int T;
    cin>>T;
    while(T--){
        ans=0;
        while(!que.empty()){
            que.pop();
        }
        cin>>n;
        bfs();
        cout<<ans<<endl;
    }
    return 0;
}

用一维数组来存储棋盘状态，简化到原先1/15的空间

 

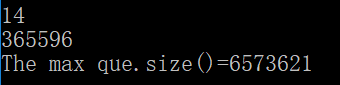
 这样就在n==14时就可以跑出结果了，可以看到队列最大的时候有六百多万个节点

不过提交还是MLE，节点还得进一步简化

ac代码

#include<iostream>
using namespace std;
#include<queue>
int n;
int ans;
struct node
{
    int step;
    int left;
    int right;
    int up;
};
queue<node> q;
void bfs()
{
    node h;
    h.step=0;
    h.left=0;
    h.right=0;
    h.up=0;
    q.push(h);
    while(!q.empty()){
        node t=q.front();
        q.pop();
        int left=t.left;
        int right=t.right;
        int up=t.up;
        left>>=1;//棋盘上左移一列
        right<<=1;
        for(int i=1;i<=n;i++){
            int now=(1<<(i-1));//当前列
            if(!(now&left)&&!(now&right)&&!(now&up)){
                h.step=t.step+1;
                h.left=(now|left);
                h.right=(now|right);
                h.up=(now|up);
                if(h.step==n){
                    ans++;
                }
                else{
                    q.push(h);
                }
            }
        }
    }
}
int main()
{
    int T;
    cin>>T;
    while(T--){
        cin>>n;
        ans=0;
        while(!q.empty()){
            q.pop();
        }
        bfs();
        if(n==1){
            ans+=1;
        }
        cout<<ans<<endl;
    }
    return 0;
}

代码分析

这里每个节点只有4个整形变量，空间上可以符合要求

step代表当前行

使用二进制来标记棋盘

int now=(1<<(i-1));

这里的now表示当前列，1、2、3...列分别用2^0、2^1、2^2...来表示

对应的

left>>=1;
right<<=1;

也分别表示在棋盘上左移一列和右移一列

而判断条件

!(now&left)&&!(now&right)&&!(now&up)

now&left、now&right、now&up全为0，结合上面left和right的操作可知，是判断当前列的左上方、正上方、右上方是否都没有皇后，若有，则条件不成立

若条件成立，则在当前位置放置皇后，即

h.step=t.step+1;
h.left=(now|left);
h.right=(now|right);
h.up=(now|up);

left>>=1;
right<<=1;