ACM/ICPC 之 最长公共子序列计数及其回溯算法(51Nod-1006(最长公共子序列))

　　这道题被51Nod定为基础题（这要求有点高啊），我感觉应该可以算作一级或者二级题目，主要原因不是动态规划的状态转移方程的问题，而是需要理解最后的回溯算法。

　　

　　题目大意：找到两个字符串中最长的子序列，子序列的要求满足其中字符的顺序和字母在两个序列中都必须相同，任意输出一个符合题意的子序列

　　首先是最基本的最长公共子序列的状态转移问题：

　　

　　这里的maxLen[i][j]数组的意思就是保存s1的前 i 个字符和s2的前 j 个字符匹配的状态。

　　举个例子：maxLen[3][6]即表明在s1的前3个字符和s2的前6个字符中匹配到的最长公共子序列的长度。

　　　　如果能够理解这里，那么动态规划的“无后效性”这一关键性质也就理解了，动态规划的关键就在于找到一个合理的最优状态使得其在后续的状态转移中不会被影响，而其状态就是题设最优问题的子优化问题，这样的状态就得以让我们逐步向父优化问题递进。

　　基于此可以将maxLen[i-1][j-1]作为maxLen[i][j]的子问题

　　　　当s1的第 i 字符和s2的第 j 字符匹配时有状态转移方程：maxLen[i][j] = maxLen[i-1][j-1] + 1

　　而maxLen[i-1][j]和maxLen[i][j-1]则是在i和j不匹配时将前一个状态的最优解传递给下一状态

　　　　即不匹配时有状态转移方程：maxLen[i][j] = max(maxLen[i-1][j], maxLen[i][]j-1)

　　以下给出基于此状态转移方程的计数代码

//两字符串中找出一个最长字符串
//ps:其字符在两字符串中存在且顺序相同-记录字符个数

#define max(x,y) ((x)>(y)?(x):(y))

int maxlen[MAX][MAX];    //s1前i个字符和s2前i个字符最长匹配

int Matching(char s1[],char s2[])
{
    memset(maxlen, 0, sizeof(maxlen));
    int len1 = strlen(s1);
    int len2 = strlen(s2);
    for (i = 1; i <= len1; i++)
        for (j = 1; j <= len2; j++)
            if (s1[i - 1] == s2[j - 1])    //s1前i与s2前j字符串尾字符匹配
                maxlen[i][j] = maxlen[i - 1][j - 1] + 1;
            else            //不匹配
                maxlen[i][j] = max(maxlen[i][j - 1], maxlen[i - 1][j]);
    return maxlen[len1][len2];
}e

---

　　接着是该题最重要的回溯算法，这一步是输出子序列的关键：

　　　　借用一张图描述该算法思路如下：

　　　　

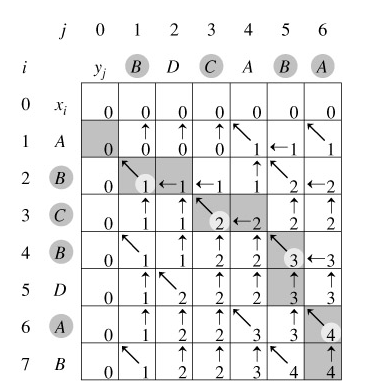
　　　　要从标明了各状态的二维数组中找出子序列的方法可以作如下描述：

　　　　　　当父状态maxLen[i][j]和最相近的两个子状态maxLen[i-1][j]和maxLen[i][j-1]都不相同的时候

　　　　　　　　说明此时maxLen[i][j]做了该运算：maxLen[i][j] = maxLen[i-1][j-1] + 1

　　　　　　当父状态maxLen[i][j]和最相近的两个子状态中任一个相同的时候

　　　　　　　　说明此时maxLen[i][j]做了该运算：maxLen[i][j] = max(maxLen[i-1][j], maxLen[i][]j-1)　　

　　　　

　　　　需要注意的是在父状态和最近子状态都相同时将衍生平移的两个方向，由此可以得出所有最长公共子序列的集合。

　　　　由于该题只需要输出任一个，因此指定一个方向回溯即可。

---

　　因此合并上述的两个算法可以得出该题的最终算法：

　　

//求出最长公共子序列并输出任一子序列
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

#define MAX 1001
#define max(x,y) ((x)>(y)?(x):(y))

char s1[MAX], s2[MAX];
int maxLen[MAX][MAX];
char ans[MAX];

int main()
{
    int k = 0;
    scanf("%s%s", s1,s2);
    int len1 = strlen(s1);  
    int len2 = strlen(s2);
    
    for (int i = 1; i <= len1; i++)
    {
        for (int j = 1; j <= len2; j++)
        {
            if (s1[i-1] == s2[j-1])
                maxLen[i][j] = maxLen[i - 1][j - 1] + 1;
            else maxLen[i][j] = max(maxLen[i][j - 1], maxLen[i-1][j]);
        }
    }
    
    int i = len1;
    int j = len2;
    while(i)
    {
        if (maxLen[i][j] > maxLen[i - 1][j])
        {
            if (maxLen[i][j] > maxLen[i][j - 1])
                ans[maxLen[i][j] - 1] = s1[i - 1];
            else i++;    //左平移
            j--;    //减小一个规模
        }
        i--;    //上平移
    }
    
    printf("%s
", ans);
    return 0;
}