时刻要记住正难则反,可以知道总数是 (26^m),我们可以减掉不合法的。
AC自动机上面dp,不合法的显然就是没有出现任意的一个串,根据rainy的教导
单词 (b,bce,abcd) 的 ACAM

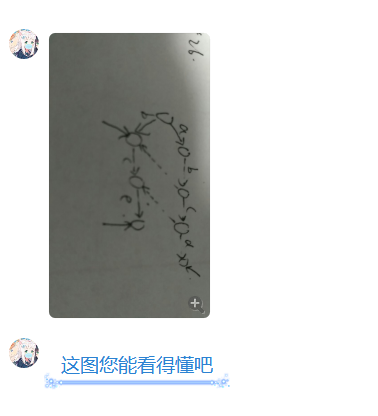

然后 (dp) 就好了,由于点数不超过 (n*m leq 6000),然后你每一位枚举复杂度是 (m^2n) 的
可以通过本题
// powered by c++11
// by Isaunoya
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); ++i)
#define Rep(i, x, y) for (register int i = (x); i >= (y); --i)
using namespace std;
using db = double;
using ll = long long;
using uint = unsigned int;
#define Tp template
using pii = pair<int, int>;
#define fir first
#define sec second
Tp<class T> void cmax(T& x, const T& y) {if (x < y) x = y;} Tp<class T> void cmin(T& x, const T& y) {if (x > y) x = y;}
#define all(v) v.begin(), v.end()
#define sz(v) ((int)v.size())
#define pb emplace_back
Tp<class T> void sort(vector<T>& v) { sort(all(v)); } Tp<class T> void reverse(vector<T>& v) { reverse(all(v)); }
Tp<class T> void unique(vector<T>& v) { sort(all(v)), v.erase(unique(all(v)), v.end()); }
const int SZ = 1 << 23 | 233;
struct FILEIN { char qwq[SZ], *S = qwq, *T = qwq, ch;
#ifdef __WIN64
#define GETC getchar
#else
char GETC() { return (S == T) && (T = (S = qwq) + fread(qwq, 1, SZ, stdin), S == T) ? EOF : *S++; }
#endif
FILEIN& operator>>(char& c) {while (isspace(c = GETC()));return *this;}
FILEIN& operator>>(string& s) {while (isspace(ch = GETC())); s = ch;while (!isspace(ch = GETC())) s += ch;return *this;}
Tp<class T> void read(T& x) { bool sign = 0;while ((ch = GETC()) < 48) sign ^= (ch == 45); x = (ch ^ 48);
while ((ch = GETC()) > 47) x = (x << 1) + (x << 3) + (ch ^ 48); x = sign ? -x : x;
}FILEIN& operator>>(int& x) { return read(x), *this; } FILEIN& operator>>(ll& x) { return read(x), *this; }
} in;
struct FILEOUT {const static int LIMIT = 1 << 22 ;char quq[SZ], ST[233];int sz, O;
~FILEOUT() { flush() ; }void flush() {fwrite(quq, 1, O, stdout); fflush(stdout);O = 0;}
FILEOUT& operator<<(char c) {return quq[O++] = c, *this;}
FILEOUT& operator<<(string str) {if (O > LIMIT) flush();for (char c : str) quq[O++] = c;return *this;}
Tp<class T> void write(T x) {if (O > LIMIT) flush();if (x < 0) {quq[O++] = 45;x = -x;}
do {ST[++sz] = x % 10 ^ 48;x /= 10;} while (x);while (sz) quq[O++] = ST[sz--];
}FILEOUT& operator<<(int x) { return write(x), *this; } FILEOUT& operator<<(ll x) { return write(x), *this; }
} out;
#define int long long
int n , m ;
const int maxn = 66 ;
const int maxm = 111 ;
int dp[maxm][maxn * maxm] ;
const int mod = 10007 ;
int qpow(int x , int y) {
int ans = 1 ;
for( ; y ; y >>= 1 , x = x * x % mod)
if(y & 1)
ans = ans * x % mod ;
return ans ;
}
struct ACAM {
int ch[maxn * maxm][26] , fail[maxn * maxm] , ed[maxn * maxm] , cnt = 1 ;
void ins(string s) {
int p = 1 ;
for(char x : s) {
int c = x - 'A' ;
if(! ch[p][c]) ch[p][c] = ++ cnt ;
p = ch[p][c] ;
}
ed[p] |= 1 ;
}
void build() {
queue < int > q ;
for(int i = 0 ; i < 26 ; i ++)
if(ch[1][i])
fail[ch[1][i]] = 1 , q.push(ch[1][i]) ;
else
ch[1][i] = 1 ;
while(! q.empty()) {
int u = q.front() ;
q.pop() ;
for(int i = 0 ; i < 26 ; i ++)
if(ch[u][i])
fail[ch[u][i]] = ch[fail[u]][i] , ed[ch[u][i]] |= ed[fail[ch[u][i]]] , q.push(ch[u][i]) ;
else
ch[u][i] = ch[fail[u]][i] ;
}
}
int solve() {
memset(dp , 0 , sizeof(dp)) ;
dp[0][1] = 1 ;
rep(i , 0 , m - 1)
rep(j , 1 , cnt)
rep(k , 0 , 25)
if(! ed[ch[j][k]])
(dp[i + 1][ch[j][k]] += dp[i][j]) %= mod ;
int qwq = 0 ;
rep(i , 1 , cnt) (qwq += dp[m][i]) %= mod ;
return qwq ;
}
} acam ;
signed main() {
// code begin.
in >> n >> m ;
rep(i , 1 , n) {
string s ;
in >> s ;
acam.ins(s) ;
}
acam.build() ;
int ans = qpow(26 , m) ;
(ans += mod - acam.solve()) %= mod ;
out << ans << '
' ;
return 0;
// code end.
}