题目描述:
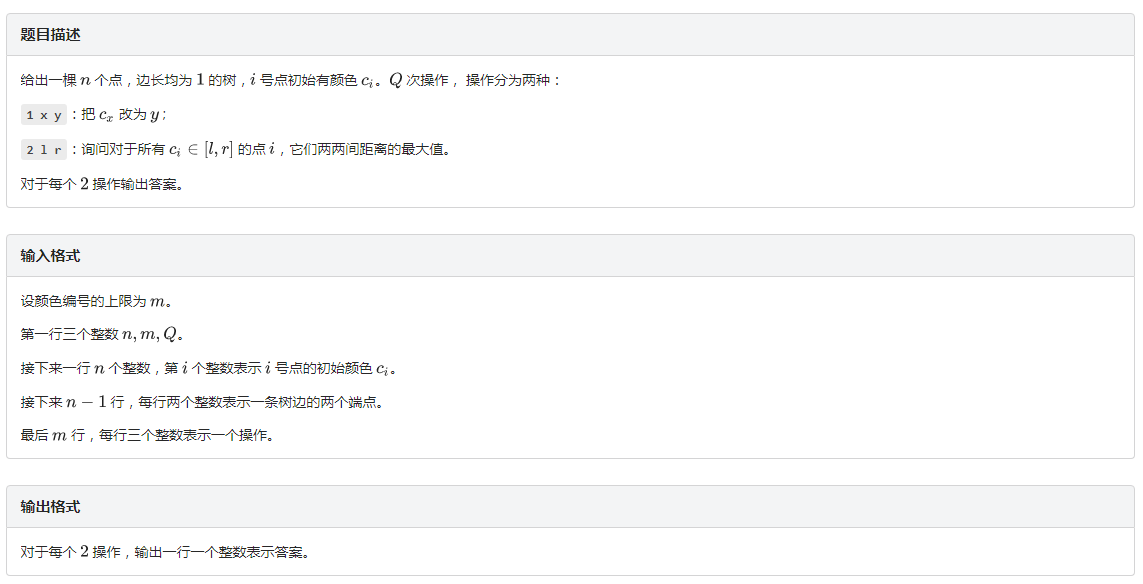

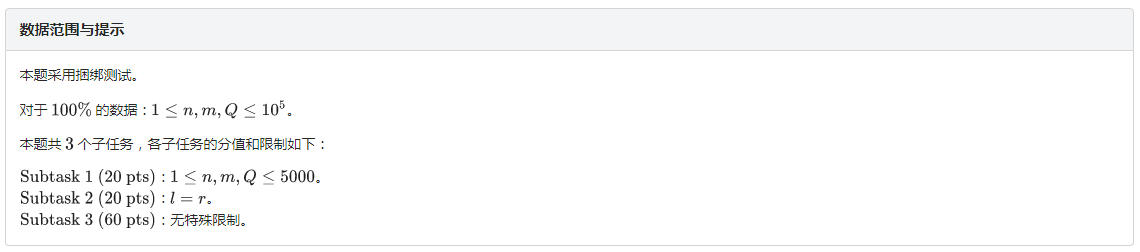
分析:
签到题想半天,人没了
将两个点集合并维护直径,两个点集分别的直径一共四个端点两两距离最大即为直径
区间点集合并,联想到线段树,每个区间两个值表示这个区间点集合并出的端点,简单维护
考虑颜色变化导致的点集内部插入删除
加入很好维护,删除不行
每种颜色动态开点线段树,依葫芦画瓢维护
巨佬们说可以直接一发平衡树,按颜色排序,支持插入删除,维护区间直径
好像Splay和非旋Treap都可以维护
也是可以做的,只不过我平衡树太菜了,写的动态开点
我的复杂度是\(O(nlog^2n)\),写了\(O(1)\)求LCA深度之后就可以减到\(O(nlogn)\)
(怎么我\(O(nlog^2n)\)比写\(O(nlogn)\)的平衡树快啊2333
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<string>
#define maxn 200005
#define INF 0x3f3f3f3f
using namespace std;
inline int getint()
{
int num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n,m,Q;
int fir[maxn],nxt[maxn<<1],to[maxn<<1],cnt;
int sz[maxn],fa[maxn],dpt[maxn],son[maxn],tp[maxn];
int C[maxn],rt[maxn],tot;
int lc[maxn<<6],rc[maxn<<6];
inline void newnode(int u,int v)
{to[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;}
inline void dfs1(int u)
{
sz[u]=1;
for(int i=fir[u];i;i=nxt[i])if(to[i]!=fa[u])
{
fa[to[i]]=u,dpt[to[i]]=dpt[u]+1;
dfs1(to[i]),sz[u]+=sz[to[i]];
if(sz[son[u]]<sz[to[i]])son[u]=to[i];
}
}
inline void dfs2(int u,int ac)
{
tp[u]=ac;if(son[u])dfs2(son[u],ac);
for(int i=fir[u];i;i=nxt[i])if(to[i]!=fa[u]&&to[i]!=son[u])dfs2(to[i],to[i]);
}
inline int LCA(int u,int v)
{
while(tp[u]!=tp[v])
{
if(dpt[tp[u]]<dpt[tp[v]])swap(u,v);
u=fa[tp[u]];
}
return dpt[u]<dpt[v]?u:v;
}
inline int getdis(int u,int v)
{return dpt[u]+dpt[v]-2*dpt[LCA(u,v)];}
struct node{
int A,B;
inline void pushup(node x,node y)
{
if(!x.A||!y.A){A=x.A|y.A,B=x.B|y.B;return;}
int mx=-1,tmp;
if((tmp=getdis(x.A,x.B))>mx)mx=tmp,A=x.A,B=x.B;
if((tmp=getdis(y.A,y.B))>mx)mx=tmp,A=y.A,B=y.B;
if((tmp=getdis(x.A,y.A))>mx)mx=tmp,A=x.A,B=y.A;
if((tmp=getdis(x.A,y.B))>mx)mx=tmp,A=x.A,B=y.B;
if((tmp=getdis(x.B,y.A))>mx)mx=tmp,A=x.B,B=y.A;
if((tmp=getdis(x.B,y.B))>mx)mx=tmp,A=x.B,B=y.B;
}
}t[maxn<<2],p[maxn<<6],Ans;
inline void insert(int &i,int l,int r,int x,int num)
{
if(!i)i=++tot;
if(l==r){p[i].A=p[i].B=num;return;}
int mid=(l+r)>>1;
if(x<=mid)insert(lc[i],l,mid,x,num);
else insert(rc[i],mid+1,r,x,num);
p[i].pushup(p[lc[i]],p[rc[i]]);
}
inline void build(int i,int l,int r)
{
if(l==r){t[i]=p[rt[l]];return;}
int mid=(l+r)>>1;
build(i<<1,l,mid),build(i<<1|1,mid+1,r);
t[i].pushup(t[i<<1],t[i<<1|1]);
}
inline void update(int i,int l,int r,int x)
{
if(l==r){t[i]=p[rt[x]];return;}
int mid=(l+r)>>1;
if(x<=mid)update(i<<1,l,mid,x);
else update(i<<1|1,mid+1,r,x);
t[i].pushup(t[i<<1],t[i<<1|1]);
}
inline void query(int i,int l,int r,int ql,int qr)
{
if(qr<l||r<ql)return;
if(ql<=l&&r<=qr){Ans.pushup(Ans,t[i]);return;}
int mid=(l+r)>>1;
query(i<<1,l,mid,ql,qr),query(i<<1|1,mid+1,r,ql,qr);
}
int main()
{
n=getint(),m=getint(),Q=getint();
for(int i=1;i<=n;i++)C[i]=getint();
for(int i=1;i<n;i++)
{
int u=getint(),v=getint();
newnode(u,v),newnode(v,u);
}
dfs1(1),dfs2(1,1);
for(int i=1;i<=n;i++)insert(rt[C[i]],1,n,i,i);
build(1,1,m);
while(Q--)
{
int op=getint(),x=getint(),y=getint();
if(op==1)
{
insert(rt[C[x]],1,n,x,0);
update(1,1,m,C[x]);
C[x]=y;
insert(rt[C[x]],1,n,x,x);
update(1,1,m,C[x]);
}
else
{
Ans.A=Ans.B=0;
query(1,1,m,x,y);
printf("%d\n",Ans.A?getdis(Ans.A,Ans.B):0);
}
}
}
