背包问题是程序设计与算法以及竞赛中的一类重要问题。其种类繁多,也是极其经典的考点
例题:0-1背包
有N件物品以及一个容量为V的背包。放入第i件物体的代价是C(i),得到的价值是W(i)。求在不超过容量的情况下获得的最大价值。
数据范围: 1≤N≤100,1≤V≤10^6,1≤C(i)≤10000,1≤W(i)≤10000。
输入格式:
第1行两个正整数,分别表示N,V。
接下来N行分别有2个正整数C(i),W(i)。
输出格式:
一行一个正整数,为最大价值总和。
样例
#in:
4 20
8 5
9 6
5 7
2 3
#out:
16
解析:
动态规划解这类最优值问题,首先 定义状态 F{i,v}为前i件物品放入容量为V的背包中所可以取得的最大值 。那么很容易得到状态转移方程F{ i,v }=max( F { i,v },F{ i-1,v-C(i) } )
可以这样理解:
对于第i件物品,要么放,要么不放。那么可以把这个问题推到 只和前面i-1件物品放不放 有关系的问题,放即为F{ i-1,v },不放就F{ i-1,v-C(i)}加上放入i物品得到的价值W(i)。
于是,时间复杂度 O( NV ),空间复杂度 O( NV )
但是
这里开二维数组极其容易爆炸 (第一次就RE了嘤嘤嘤
并且我们可以利用滚动数组(即反复更新一个一维数组,由动态规划问题的无后效性可知状态只与上一个状态有关) 来稍微优化一下。
最终程序:
#include<bits/stdc++.h>
using namespace std;
int ci[4000],wi[4000];
int f[138800]//下标要>=c;
int main()
{
int n,c;
cin>>n>>c;
int i,j;
for(i=1;i<=n;i++)
{
cin>>ci[i]>>wi[i];
}
for(i=1;i<=n;i++)
{
for(j=c;j>=ci[i];j--)
{
f[j]=max(f[j],f[j-ci[i]]+wi[i]);
}
}
cout<<f[c];
return 0;
}
对于j循环条件,这里表示一个元素至多只取一次。
若改成:
for(j=ci[i];j<=c;j++)
则是一个元素可以无限取。(即完全背包写法)
原理: 从一维数组上区别0-1背包和完全背包差别就在循环顺序上,0-1背包必须逆序,因为这样保证了不会重复选择已经选择的物品,而完全背包是顺序,顺序会覆盖以前的状态,所以存在选择多次的情况,也符合完全背包的题意。状态转移方程为\(F[i] = max(F[i],dp[F-c[i]]+v[i])\)。
0-1背包:
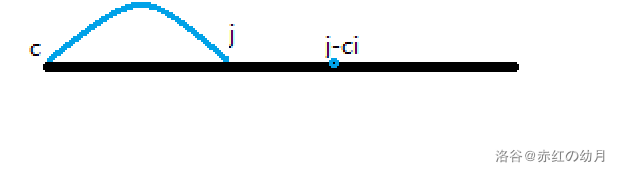
完全背包:
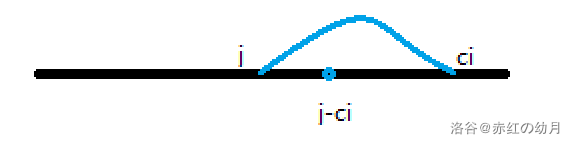
优化到这里,初等的题就完全不是问题了desu ~
另一个简单有效的优化
:若两件物品i、j满足\(c[i]=w[j]\),则将物品j去掉,不用考虑。这个优化的正确性显然:任何情况下都可将价值小费用高得j换成物美价廉的i,得到至少不会更差的方案。对于随机生成的数据,这个方法往往会大大减少物品的件数,从而加快速度。然而这个并不能改善最坏情况的复杂度,因为有可能特别设计的数据可以一件物品也去不掉。
这个优化可以简单的O(N^2)地实现,一般都可以承受。另外,针对背包问题而言,比较不错的一种方法是:首先将费用大于V的物品去掉,然后使用类似计数排序的做法,计算出费用相同的物品中价值最高的是哪个,可以O(V+N)地完成这个优化。
详情--->背包九讲
加个条件:不超过载重M(多维背包)
其实不难,只需要将循环动一下手脚,数组增一维即可。
for(int i=1;i<=n;i++)
{
for(int j=m;j>=k[i];j--)//每个元素最多只取一次
{
for(int o=x;o>=z[i];o--)
f[j][o]=max(f[j][o],f[j-k[i]][o-z[i]]+p[i]);
}
}
再来,每个物品有个数限制(即多重背包)
这个时候再加个循环枚举就是了
但是,很多时候(特别是物品多的时候)
这样会超时(如P1833樱花
所以,有一种优化方式叫做二进制优化。
基本思想:
将物品的数量以二进制拆分,分成1,2,4,8,16,32,64 ....... 再把花费和价值乘以次数即可。
例如一个物品可使用20次,则可拆为:1 , 2 , 4 , 8 , 5。
//c[i]为代价,w[i]为价值,p[i]为使用次数
for(int j=1;j<=p[i];j<<=1)/*二进制分堆,此时j相当于权重(应该是这样的 */
{
for(int k=v;k>=j*c[i];k--)
{
f[k]=max(f[k],f[k-c[i]*j]+w[i]*j);
}
p[i]-=j;//算了的就减去了;
}
if(p[i]>0)//若c还有剩余,再来次背包
{
for(int k=v;k>=c[i]*p[i];k--)
{
f[k]=max(f[k],f[k-c[i]*p[i]]+w[i]*p[i]);
}
}
这样优化后求解单个状态时间能降到O(log(C/w[i]))
分组背包
这类问题也会非常普遍,例题洛谷P1757
一般题目会告诉你,许许多多物品被分成几组,每组物品相互冲突。然后求最大价值。
这个时候,就需要将同组别物品看做一个整体,第一层循环先遍历组别。然后在第三层循环遍历组内的每组物品,且保证每组物品都只取一次。
例题AC代码:
#include <bits/stdc++.h>
using namespace std;
int v,n,t;
int w[1010],c[1010];
int a[110][1010]/*记录组别所对应的i,a[p][0]为当前组别总数*/,f[1010];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>v>>n;
for(int i=1;i<=n;i++)
{
int p;
cin>>c[i]>>w[i]>>p;
a[p][++a[p][0]]=i;//记录组别
t=p>t?p:t;//最大组号
}
for(int k=1;k<=t;k++)//遍历组别
{
for(int j=v;j>=0;j--)//01背包写法,保证只取一个
{
for(int i=1;i<=a[k][0];i++)//遍历组内每个物品
{
if(j>=c[a[k][i]])//相当于01pack中j循环的 j>=c[i],因为在上面无法判断所以移下来了
{
f[j]=max(f[j],f[j-c[a[k][i]]]+w[a[k][i]]);
}
}
}
}
cout<<f[v];
return 0;
}
这玩意卡了我一个上午 (抱头蹲防)
暂时就先总结到这里
(会时不时更新的)