GitHub地址
https://github.com/wujunjie1008/031702537.git
P2P表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30min | 15min |
| Estimate | 估计这个任务需要多少时间 | 24h | 26h |
| Development | 开发 | 5h | 2h |
| Analysis | 需求分析 (包括学习新技术) | 2h | 2h |
| Design Spec | 生成设计文档 | 15min | 30min |
| Design Review | 设计复审 | 1h | 30min |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 10min | 15min |
| Design | 具体设计 | 1h | 2h |
| Coding | 具体编码 | 4h | 6h |
| Code Review | 代码复审 | 2h | 4h |
| Test | 测试(自我测试,修改代码,提交修改) | 3h | 4h |
| Reporting | 报告 | 3h | 3h |
| Test Repor | 测试报告 | 30min | 1h |
| Size Measurement | 计算工作量 | 15min | 15min |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 30min | 15min |
| 总计 | 23.16h | 26h |
需求
实现一个多阶数独解题工具。
数独
数独盘面是个九宫,每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次,所以又称“九宫格”。
初期准备——磨刀不误砍柴工
由于这次代码的要求是要cmd命令传入参数并且需要文件输入输出的格式,因此我就去百度,没想到竟然顺便解决了我之前一直有的疑问
int main(int argc, char* argv[])
原来main()函数里的第一个参数argc正是对应用cmd命令输入参数的个数,而第二个参数argv[]对应的则是这些参数的字符串形式
参考了规定的cmd输入后,我写出了一下导入参数的代码
char* i;
char* o;
int m, n, h, l;
m = atoi(argv[2]);
n = atoi(argv[4]);
i = argv[6];
ifstream fin(i);
if (!fin.is_open())
{
cout << "输入文件不存在";
return 0;
}
o = argv[8];
ofstream fout(o);
文件输入:
h = 0;
while (!fin.eof()) { //文件输入
getline(fin, list);
if (list.length() != 2 * m && list.length() != 2 * m - 1) { //表格输入不规范,与阶数m不相符则退出
cout << "表格大小不符合";
return 0;
}
for (l = 0; l < m; l++) {
num_list[h][l] = list[l * 2] - 48;
if (num_list[h][l] < 0 || num_list[h][l]>9) { //表格输入不规范,出现非数字字符则退出
cout << "九宫格中出现不是0-9的数字";
return 0;
}
}
h++;
文件输出:
for (h = 0; h < m; h++) { //文件输出
for (l = 0; l < m; l++) {
fout << num_list[h][l];
if (l != m - 1)
fout << ' ';
else
fout << '
';
}
}
fout << '
';
解题思路——山重水复疑无路
对于我个人来说,如果让我来做数独,我比较喜欢用唯余法,及通过该格子的同一行,同一列,同一宫的数来推断出该空格可以填什么数字,而对于难度较低的数独来说,一定会有一个空格只能填一个数字,当这个数字被填入后,就会出现另一个只能填一个数字的格子,因此,我觉得可以将其应用到低阶还有难度较低的9宫格数独中。具体代码如下:
int weiyu(int m) {
cout << "使用唯余法" << endl;
int h, l;
int may_count;
int count = 0;
for (h = 0; h < m; h++) {
for (l = 0; l < m; l++) {
if (num_list[h][l] == 0)
count++;
}
}
for (h = 0; h < m; h++) {
for (l = 0; l < m; l++) {
if (num_list[h][l] == 0) {
int may_num[10] = { 0 };
may_count = m;
for (int bh = 0; bh < m; bh++) { //遍历行
if (num_list[bh][l] != 0) {
if (may_num[num_list[bh][l]] == 0)
may_count--;
may_num[num_list[bh][l]] = 1;
}
}
for (int bl = 0; bl < m; bl++) { //遍历列
if (num_list[h][bl] != 0) {
if (may_num[num_list[h][bl]] == 0)
may_count--;
may_num[num_list[h][bl]] = 1;
}
}
if (m == 4 || m == 6 || m == 8 || m == 9) { //遍历宫格
int max_h = 0, max_l = 0;
int gong_h = 0, gong_l = 0;
//定位当前格在属于第几宫格
if (m == 4 || m == 8 || m == 9) {
gong_l = (int)sqrt(m);
gong_h = (int)(m / gong_l);
}
else if (m == 6) {
gong_h = (int)sqrt(m);
gong_l = (int)(m / gong_h);
}
for (int i = 1; i < m; i++) {
max_h = i * gong_h;
if (max_h > h) {
break;
}
}
for (int i = 1; i < m; i++) {
max_l = i * gong_l;
if (max_l > l) {
break;
}
}
//开始遍历
for (int i = max_h - gong_h; i < max_h; i++) {
for (int j = max_l - gong_l; j < max_l; j++) {
if (i > 9) //消除vs编译器的警告,删去不影响代码
i = 9;
if (i < 0)
i = 0;
if (j > 9)
j = 9;
if (j < 0)
j = 0;
if (num_list[i][j] != 0) {
if (may_num[num_list[i][j]] == 0)
may_count--;
may_num[num_list[i][j]] = 1;
}
}
}
}
if (may_count == 1) { //填写数字
for (int i = 1; i <= m; i++) {
if (may_num[i] == 0) {
num_list[h][l] = i;
h = 0;
l = -1;
count--; //填写成功,未填数减一
if (count == 0) {
printf("成功
");
return 0; //完成数独,返回0
}
break;
}
}
}
}
}
}
return 1; //未完成数独,返回1
}
本以为已经大功告成的我却因为输入一道更高难度的数独题目之后,心情又跌落到了谷底。(附上原题)
0 0 8 0 9 0 0 0 0
0 7 0 0 0 0 2 8 0
0 6 4 1 0 0 3 0 9
0 0 0 8 0 5 9 0 0
5 0 0 0 0 0 0 0 1
0 0 9 3 0 4 0 0 0
8 0 2 0 0 7 5 6 0
0 9 7 0 0 0 0 1 0
0 0 0 0 6 0 7 0 0
唯余法是可以用,但是一旦出现解不唯一,或者没有格子是填唯一一个数的时候唯余法根本无法解出答案。仅仅只是做出简单数独,那和咸鱼有什么区别,于是我又开始寻找新的方法。
解题思路——柳暗花明又一村
自闭是想新方法时候的主旋律,脑子在想的是总不能一格一格的试过去吧。后来无意间听到周围的人都在说DFS(深度优先算法),当时还很困惑,DFS和数独有什么关系。再后来发现DFS不正是把每一种可能都试过去嘛。但是我对于DFS的运行时间还是有着一丝担忧。抱着试试看的心态,我开始写DFS的函数。
——首先是检查函数,我在原来唯余法的基础上进行改变,就得出现在的check()函数:
int check(int h, int l, int m) {
int num[10] = { 0 };
for (int bh = 0; bh < m; bh++) { //遍历行,寻找重复的数字
if (num_list[bh][l] != 0) {
num[num_list[bh][l]]++;
if (num[num_list[bh][l]] > 1)
return 0;
}
}
for (int i = 0; i < 10; i++) {
num[i] = 0;
}
for (int bl = 0; bl < m; bl++) { //遍历列,寻找重复的数字
if (num_list[h][bl] != 0) {
num[num_list[h][bl]]++;
if (num[num_list[h][bl]] > 1)
return 0;
}
}
for (int i = 0; i < 10; i++) {
num[i] = 0;
}
if (m == 4 || m == 8 || m == 9 || m == 6) { //检验九宫格,寻找重复的数字
//定位该单元格所属的宫格
int max_h = 0, max_l = 0;
int gong_h = 0, gong_l = 0;
if (m == 4 || m == 8 || m == 9) {
gong_l = (int)sqrt(m);
gong_h = (int)(m / gong_l);
}
else if (m == 6) {
gong_h = (int)sqrt(m);
gong_l = (int)(m / gong_h);
}
for (int i = 1; i < m; i++) {
max_h = i * gong_h;
if (max_h > h) {
break;
}
}
for (int i = 1; i < m; i++) {
max_l = i * gong_l;
if (max_l > l) {
break;
}
}
//正式开始遍历
for (int i = max_h - gong_h; i < max_h; i++) {
for (int j = max_l - gong_l; j < max_l; j++) {
if (num_list[i][j] != 0) {
num[num_list[i][j]]++;
if (num[num_list[i][j]] > 1)
return 0; //有重复,返回0
}
}
}
}
return 1; //无重复,返回1
}
——接着就是我们的主角DFS(深度优先搜索)函数了:
int DFS(int n, int m){
if (n > (m*m)) {
return 1;
}
if (num_list[n / m][n % m] != 0){ // 不需要填数字,则跳过
if (DFS(n + 1, m) == 1)
return 1;
}
else{
for (int i = 1; i <= m; i++){ //试填1-9的数字
num_list[n / m][n % m] = i;
if (check(n / m, n % m, m) == 1){
if (DFS(n + 1, m) == 1)
return 1; //返回时如果构造成功,则返回1
else
num_list[n / m][n % m] = 0;
}
else
num_list[n / m][n % m] = 0;
}
}
return 0;
}
没想到看似复杂的思想在用代码实现后可以这么短,最后的结果就是成功的,更高难度的数独也被我拿下了。
3 5 8 7 9 2 1 4 6
9 7 1 4 3 6 2 8 5
2 6 4 1 5 8 3 7 9
7 2 6 8 1 5 9 3 4
5 4 3 6 7 9 8 2 1
1 8 9 3 2 4 6 5 7
8 1 2 9 4 7 5 6 3
6 9 7 5 8 3 4 1 2
4 3 5 2 6 1 7 9 8
寻求改进
一方面出于对DFS运行速度的不放心,另一方面不想让我之前写的唯余法函数就这个被删除,我开始用vs自带的性能探查器探查他们运行时间的对比:
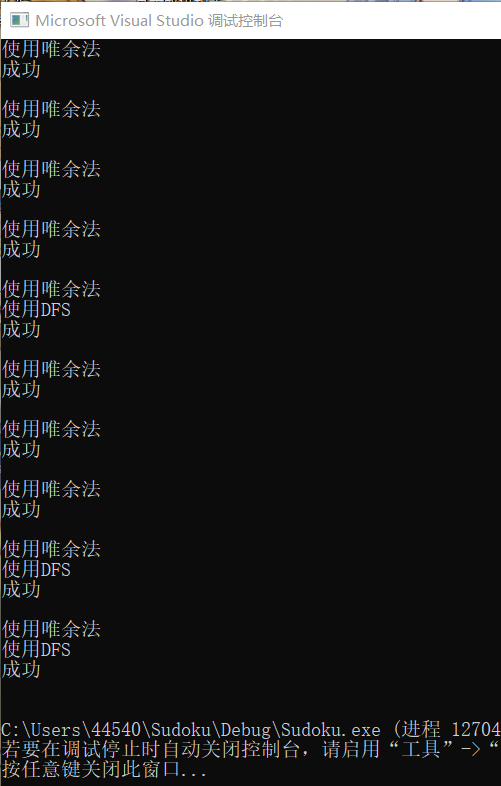
——首先是单独使用DFS的函数运行时间:

——接着是先使用唯余法若无解再使用DFS的函数运行时间:

可以看出尽管测试问题中,只有三个问题一定需要用到DFS,但是使用唯余法加DFS的策略明显比单纯用dfs要来的快,因此证明唯余法和DFS结合在时间上具有更高的效率。
单元测试
void test(int m) {
int h, l;
int may_num[10] = {0};
for (h = 0; h < m; h++) {
for (l = 0; l < m; l++) {
if (num_list[h][l] == 0) {
cout << "失败" << endl;
return;
}
else {
for (int i = 1; i < 10; i++)
may_num[i] = 0;
for (int bh = 0; bh < m; bh++) { //遍历行
if (num_list[bh][l] != 0) {
may_num[num_list[bh][l]] ++;
if (may_num[num_list[bh][l]] > 1){
cout << "行失败" <<bh<<' '<<l<< endl;
return;
}
}
}
for (int i = 1; i < 10; i++)
may_num[i] = 0;
for (int bl = 0; bl < m; bl++) { //遍历列
if (num_list[h][bl] != 0) {
may_num[num_list[h][bl]] ++;
if (may_num[num_list[h][bl]] > 1) {
cout << "列失败" << h << ' ' << bl << endl;
return;
}
}
}
for (int i = 1; i < 10; i++)
may_num[i] = 0;
if (m == 4 || m == 6 || m == 8 || m == 9) { //遍历宫格
int max_h = 0, max_l = 0;
int gong_h = 0, gong_l = 0;
//定位当前格在属于第几宫格
if (m == 4 || m == 8 || m == 9) {
gong_l = (int)sqrt(m);
gong_h = (int)(m / gong_l);
}
else if (m == 6) {
gong_h = (int)sqrt(m);
gong_l = (int)(m / gong_h);
}
for (int i = 1; i < m; i++) {
max_h = i * gong_h;
if (max_h > h) {
break;
}
}
for (int i = 1; i < m; i++) {
max_l = i * gong_l;
if (max_l > l) {
break;
}
}
//开始遍历
for (int i = max_h - gong_h; i < max_h; i++) {
for (int j = max_l - gong_l; j < max_l; j++) {
if (num_list[i][j] != 0) {
may_num[num_list[i][j]] ++;
if (may_num[num_list[i][j]] > 1) {
cout << "宫失败" << i << ' ' << j << endl;
return;
}
}
}
}
}
}
}
}
cout << "成功"<<endl<<endl;
}
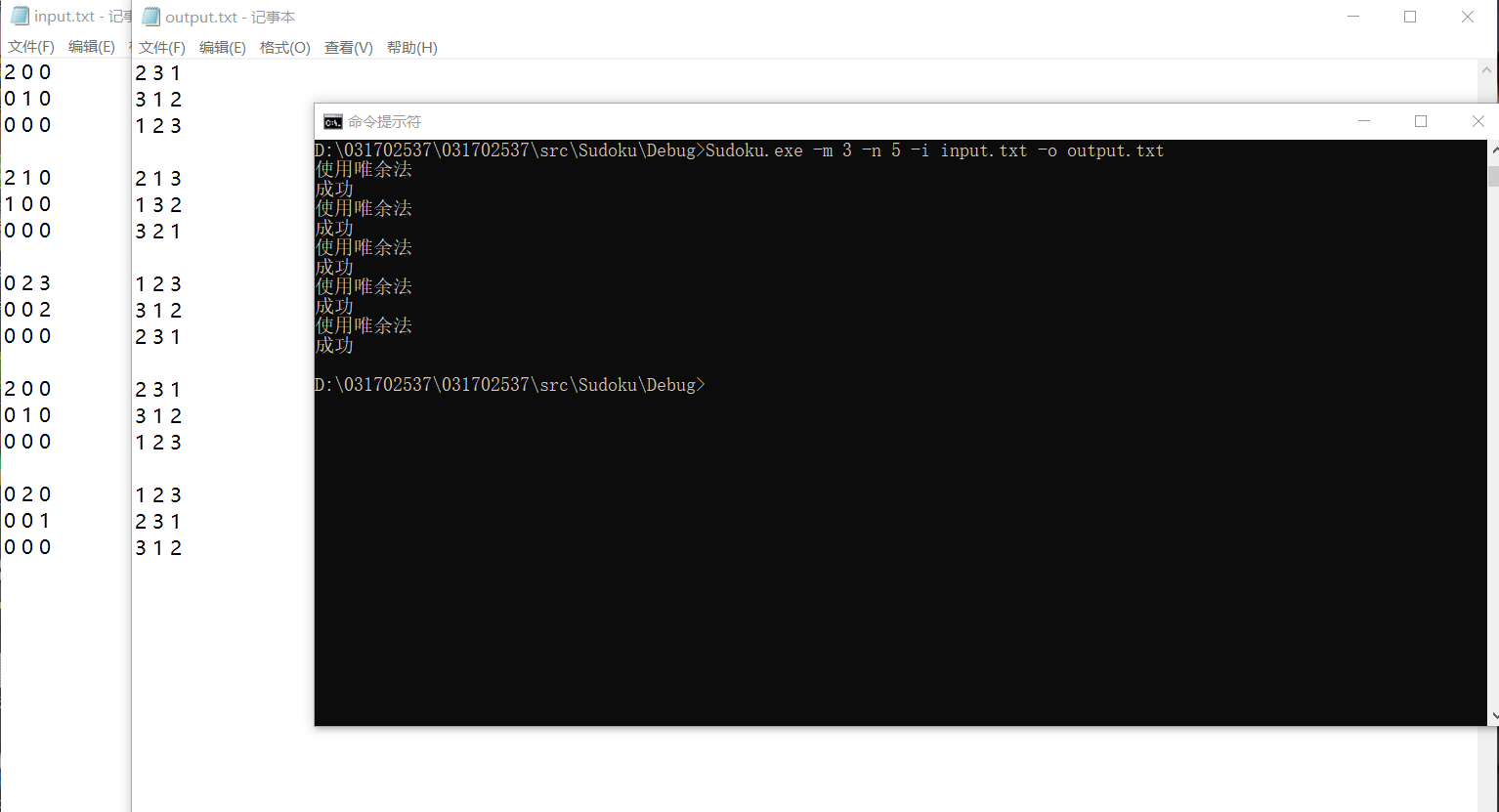
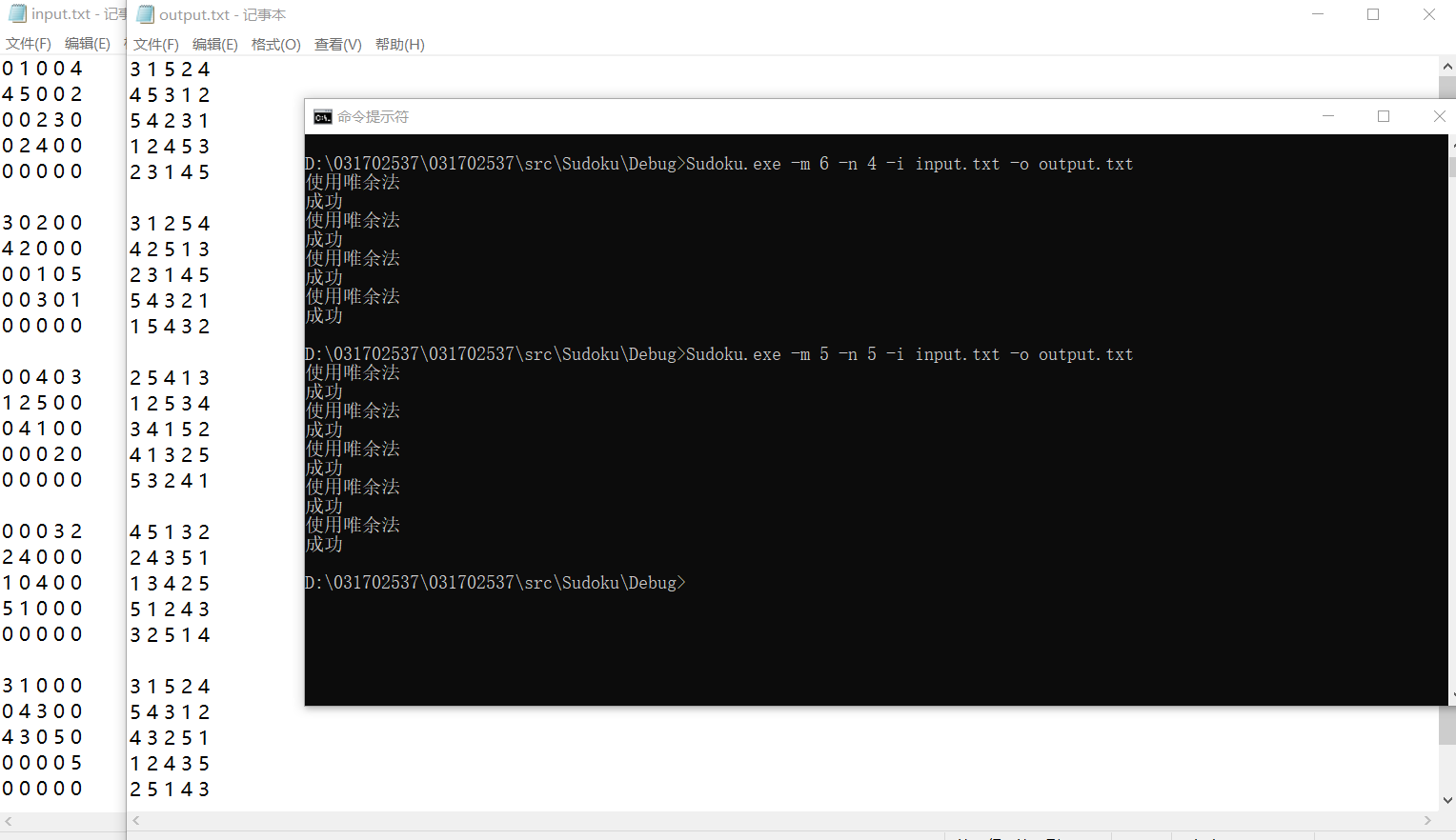
以上是我用来检验DFS的测试函数,当出现错误时,效果如下:

3阶:
4阶:

5阶:
6阶:
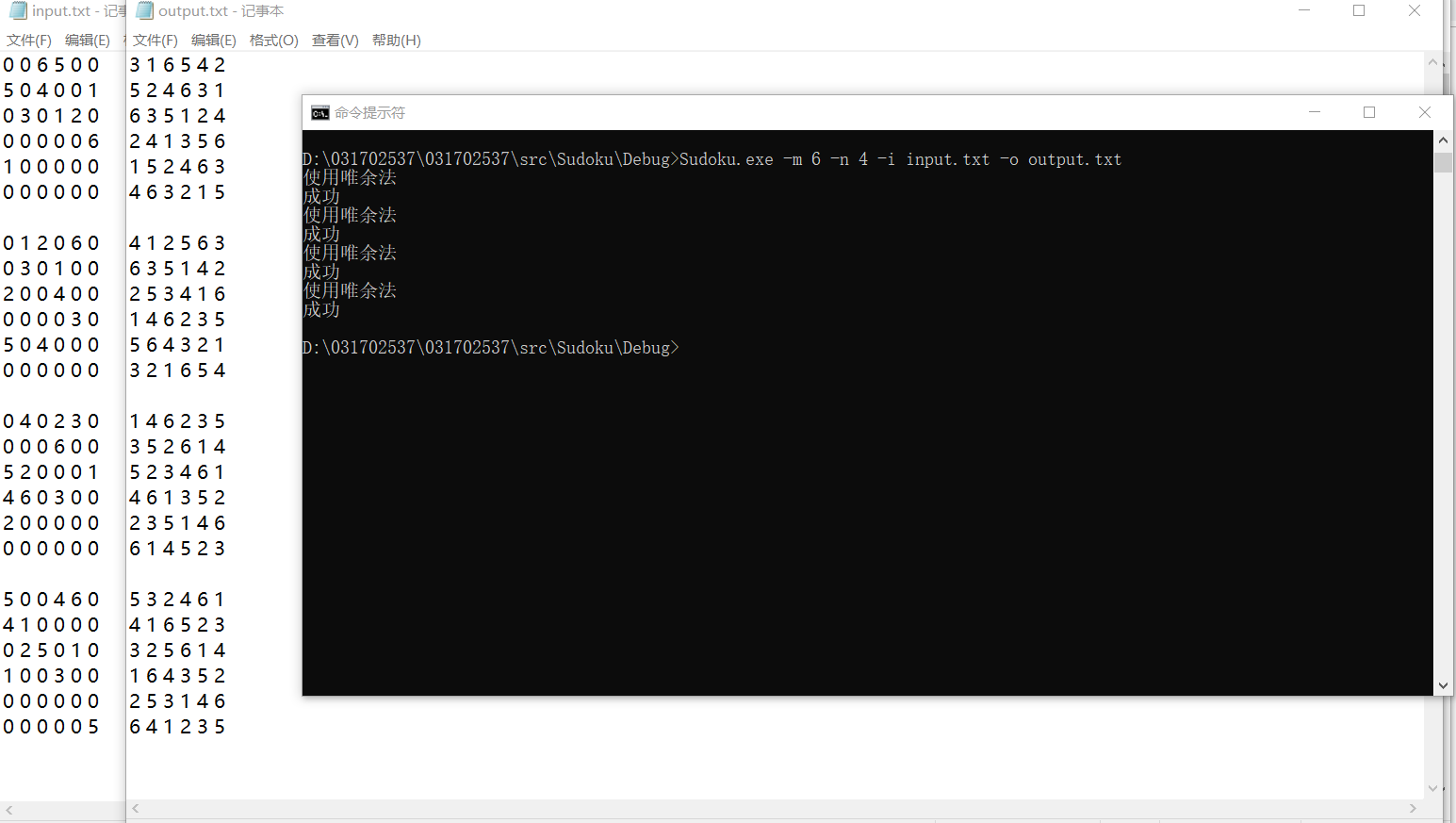
7阶:
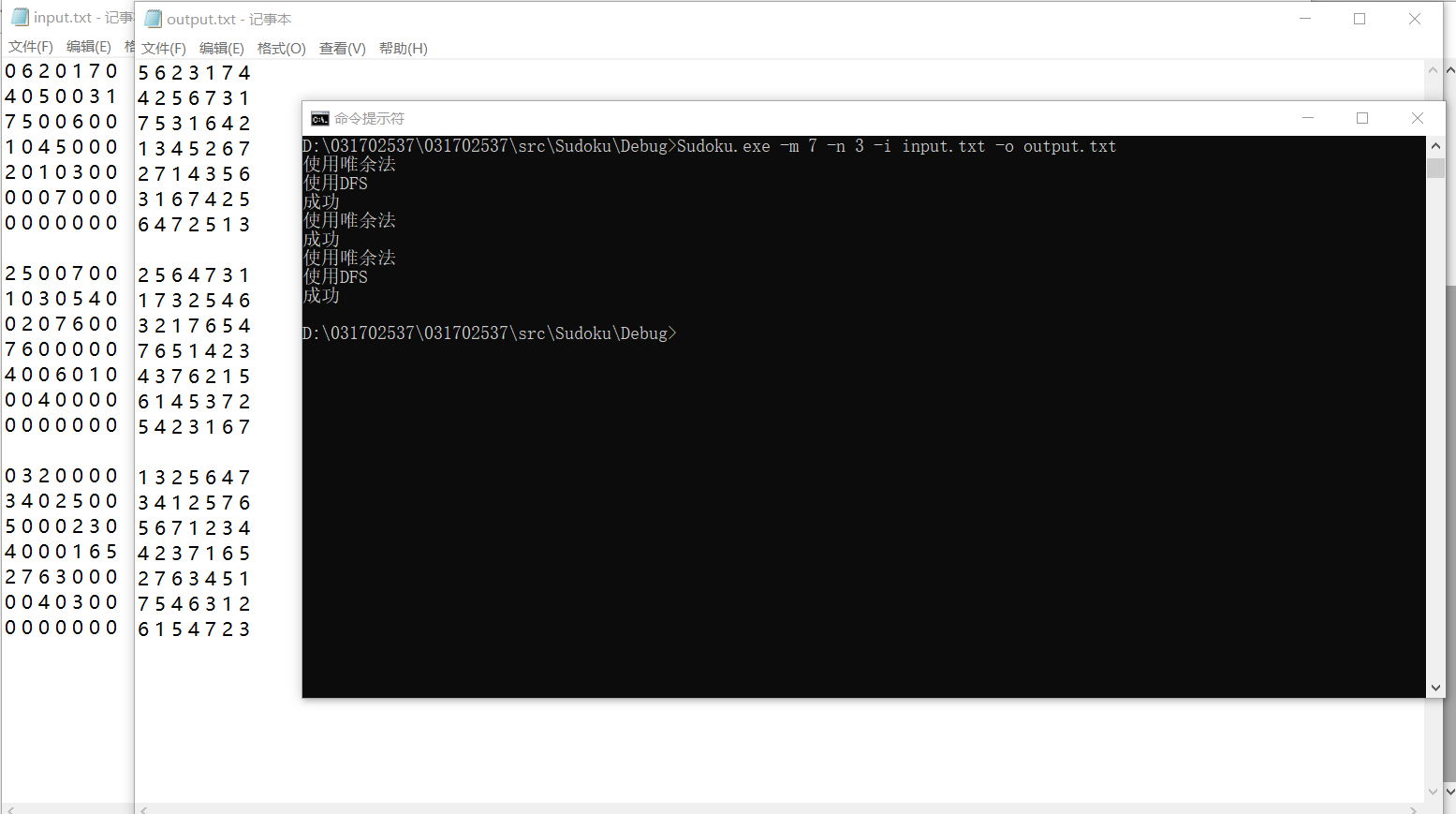
8阶:
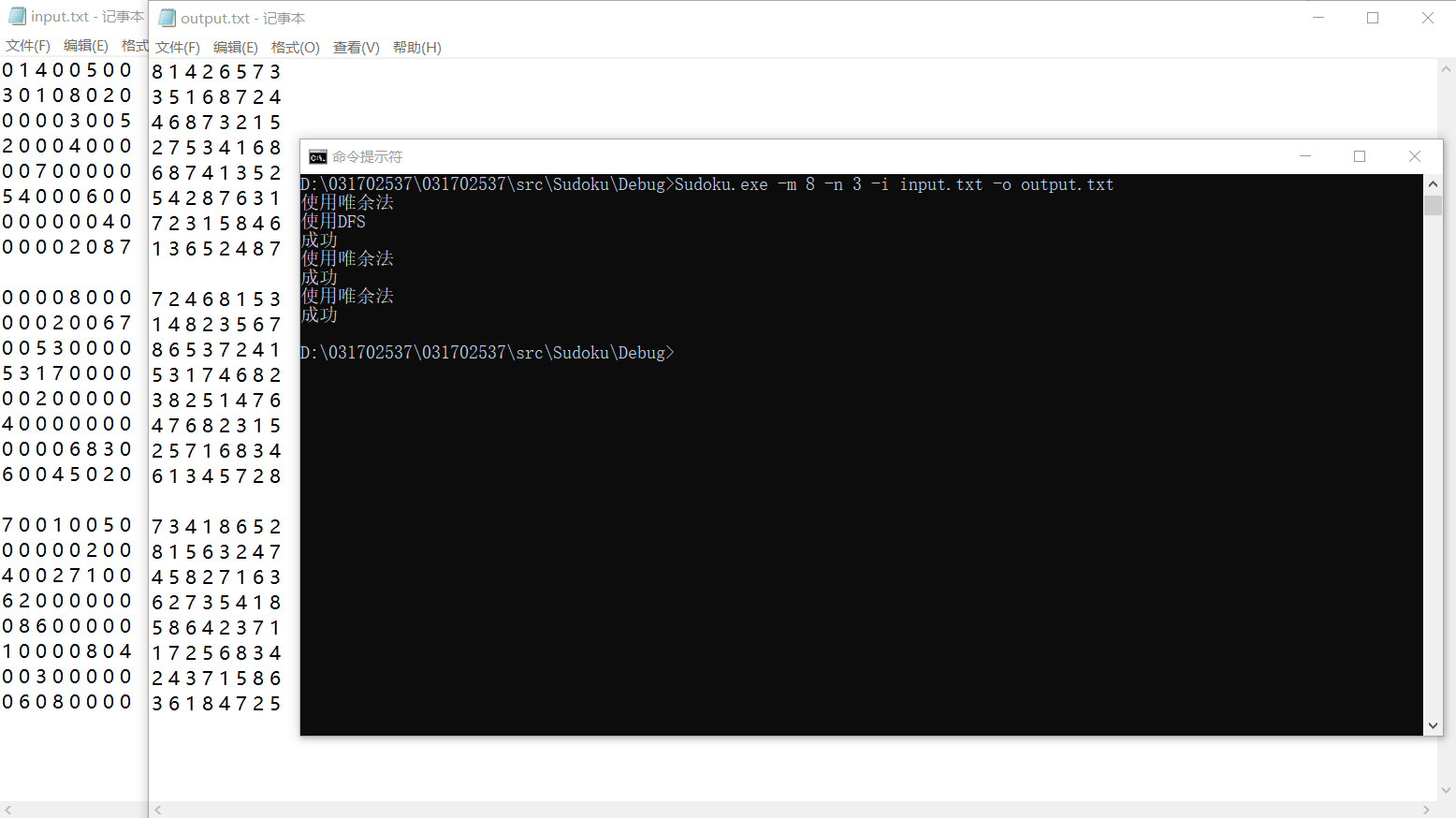
9阶:

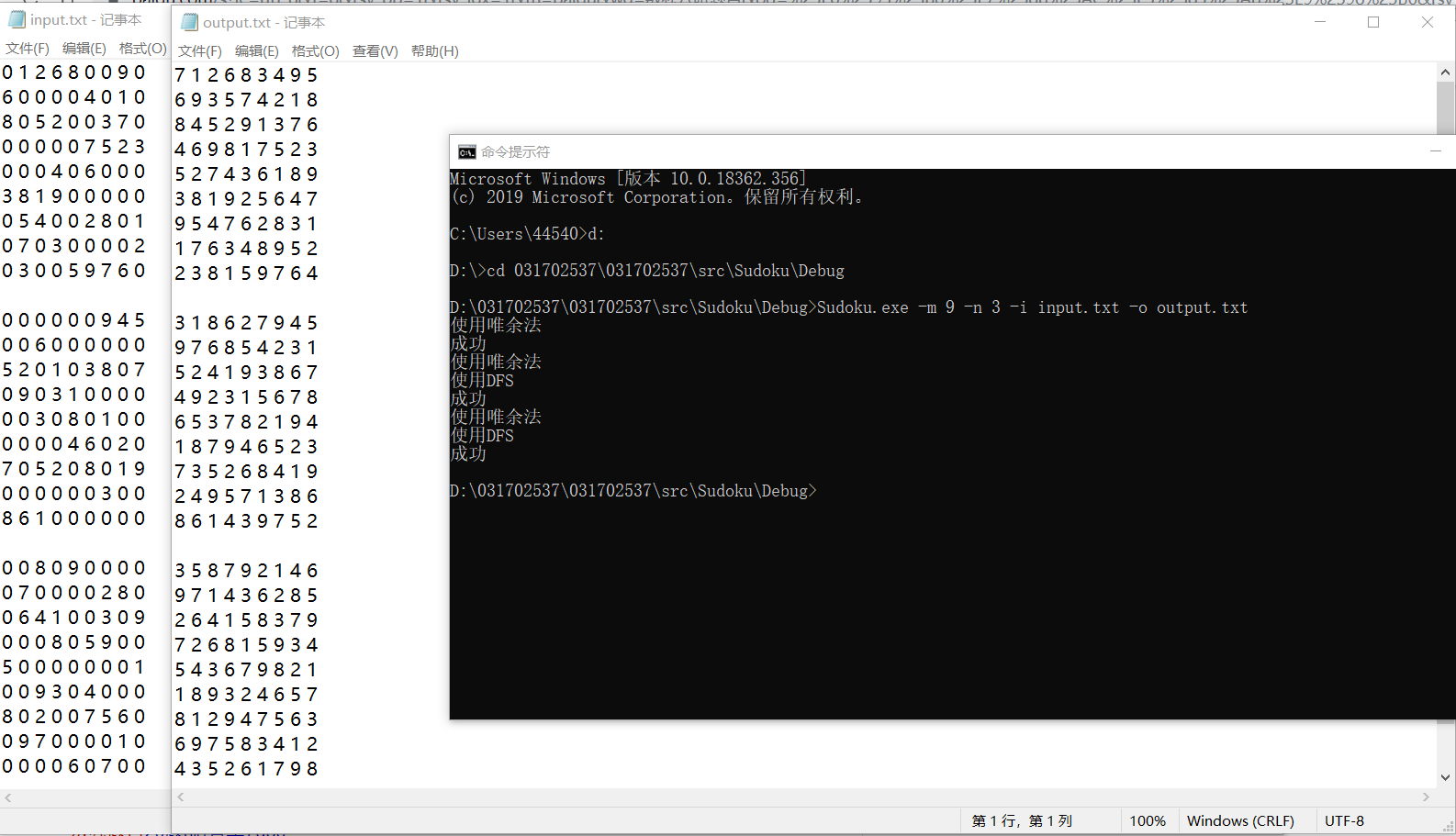
 、
、
总结
通过这次的实践作业,我学会了对于自己的项目,不仅仅要做出来,还需要对其debug,做多次测试,以及优化,就像我最后引入了DFS算法一样,而且我还学会了用VS2017的性能探查器来对代码的各个部分做出检测,来优化我的代码。不仅如此,我还学会应该合理分配我的时间,我是在距离deadline还有4天的时候才开始做的,做起来就像在和时间赛跑,所以还有很多地方做的不足,在之后的作业中这点还是需要注意。