NOIPDay1T2
(同样位置,咋和天天爱跑步差距这么大呢)
题目描述
有n个同学(编号为1到n)正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为i的同学的信息传递对象是编号为Ti同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息,但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入输出格式
输入格式:
输入共2行。
第1行包含1个正整数n表示n个人。
第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i
的同学的信息传递对象是编号为Ti的同学,Ti≤n且Ti≠i
数据保证游戏一定会结束。
输出格式:
输出共 1 行,包含 1 个整数,表示游戏一共可以进行多少轮。
输入输出样例
输入样例#1:
5 2 4 2 3 1
输出样例#1:
3
说明
样例1解释
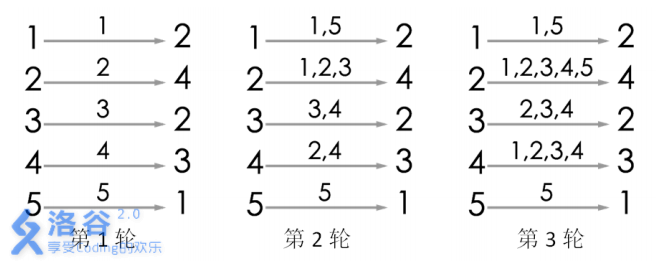
游戏的流程如图所示。当进行完第 3 轮游戏后, 4 号玩家会听到 2 号玩家告诉他自
己的生日,所以答案为 3。当然,第 3 轮游戏后, 2 号玩家、 3 号玩家都能从自己的消息
来源得知自己的生日,同样符合游戏结束的条件。
对于 30%的数据, n ≤ 200;
对于 60%的数据, n ≤ 2500;
对于 100%的数据, n ≤ 200000。
思路:DFS
题目很明显是要求找环。
代码实现:
1 #include<cstdio> 2 const int maxn=1e5*2+10; 3 int n,ans=maxn; 4 int t[maxn]; 5 int d[maxn]; 6 bool v[maxn]; 7 inline int min_(int x,int y){return x<y?x:y;} 8 void dfs(int k,int de){ 9 if(v[k]) return; 10 if(d[k]){ 11 ans=min_(ans,de-d[k]); 12 return; 13 } 14 else{ 15 d[k]=de; 16 dfs(t[k],de+1); 17 v[t[k]]=1; 18 } 19 } 20 int main(){ 21 scanf("%d",&n); 22 for(int i=1;i<=n;i++) scanf("%d",&t[i]); 23 for(int i=1;i<=n;i++) 24 if(!v[i]){ 25 dfs(i,1); 26 v[i]=1; 27 } 28 printf("%d ",ans); 29 return 0; 30 }
题目来源:洛谷