归并排序

1、基本思想

　　归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

2、图解

　　1）归并排序流程

　　

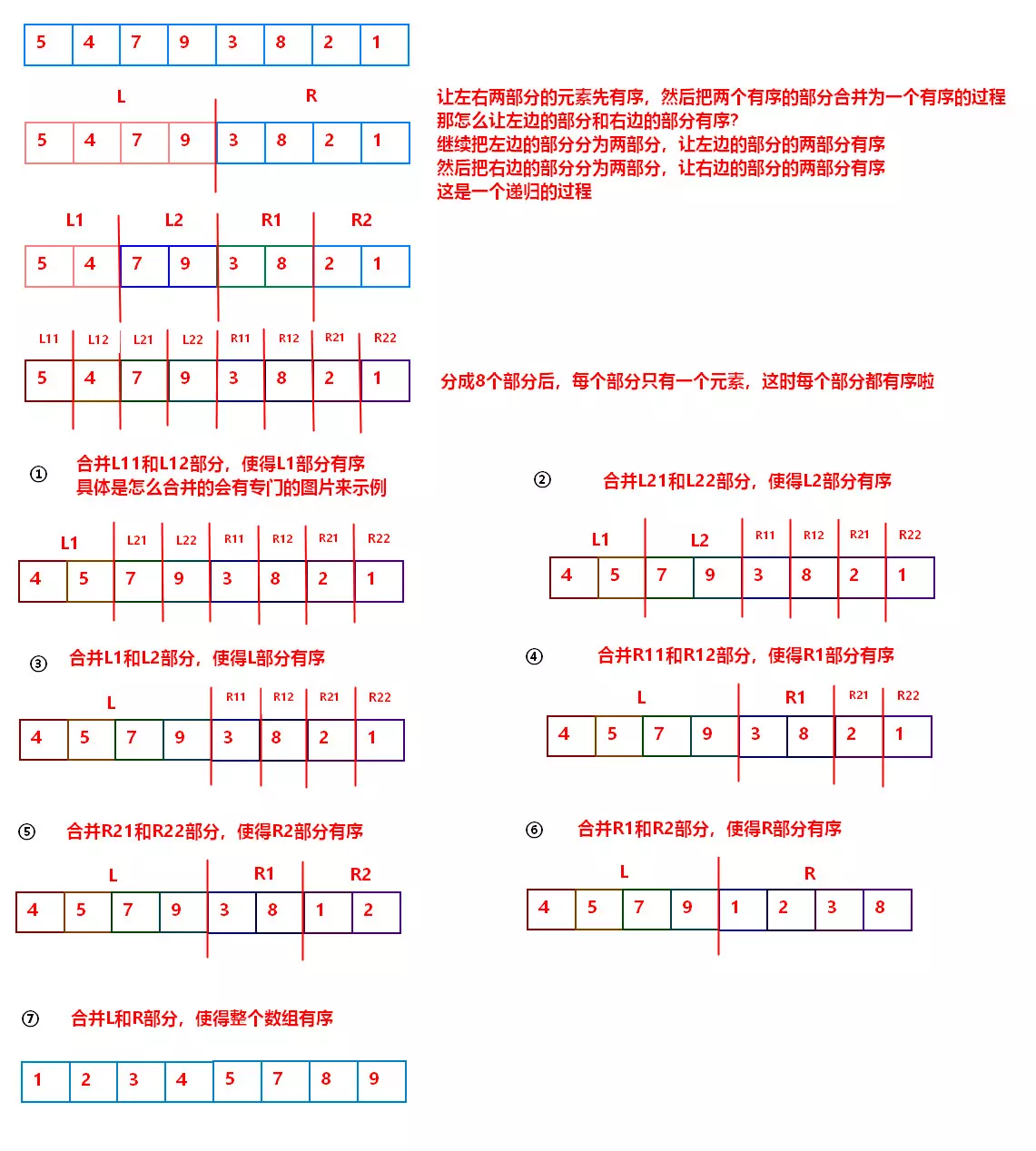
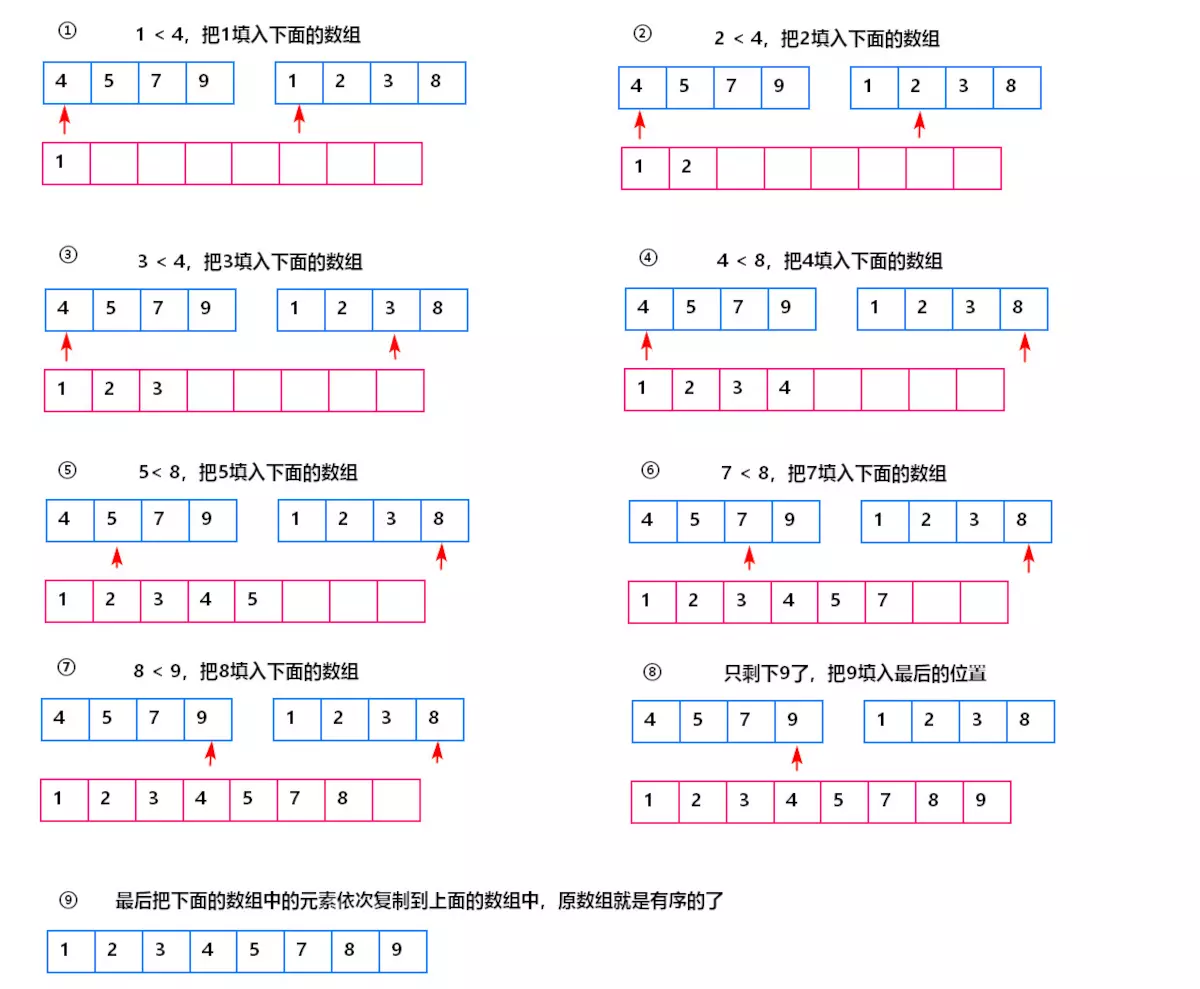
 　　2）合并两个有序数组流程

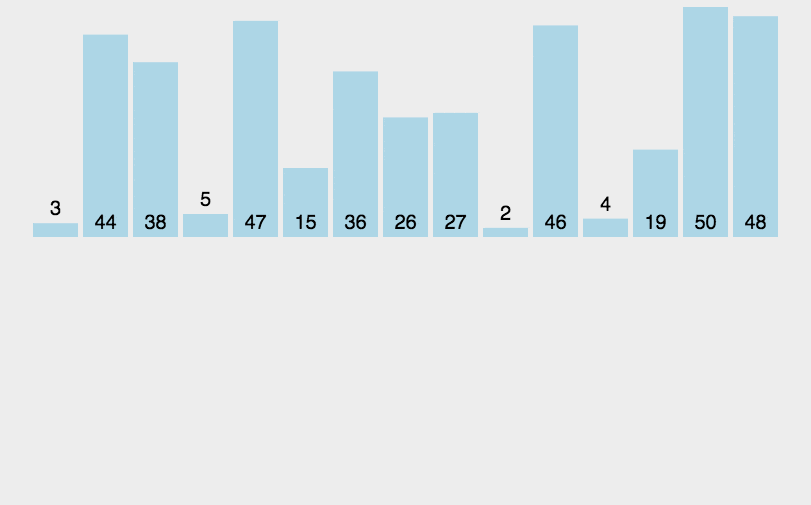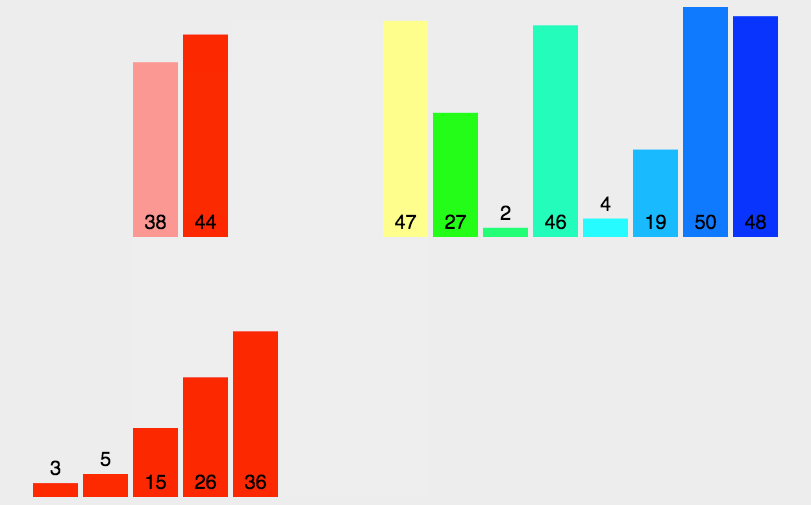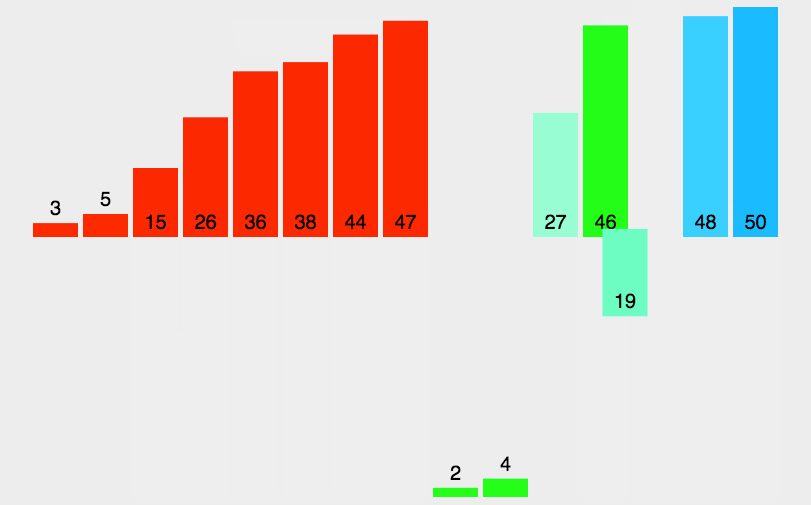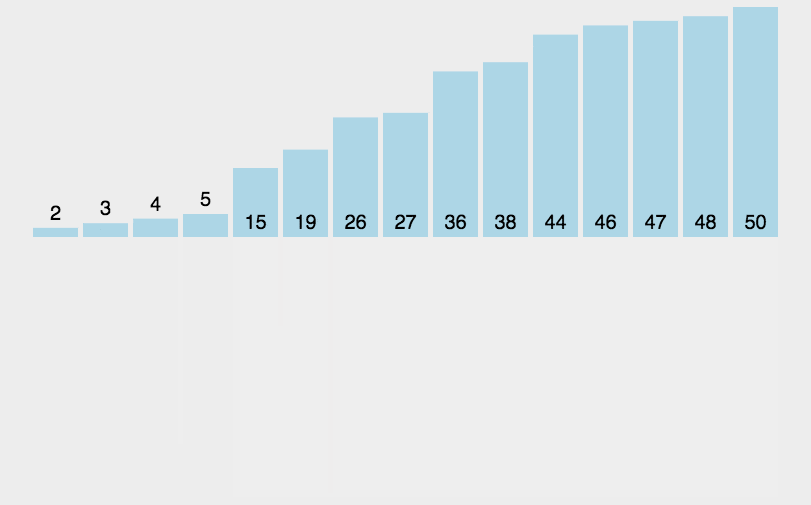
 　　3）动图演示

 3、python代码演示

def merge(arr, l, m, r): 
    n1 = m - l + 1
    n2 = r- m 
  
    # 创建临时数组
    L = [0] * (n1)
    R = [0] * (n2)
  
    # 拷贝数据到临时数组 arrays L[] 和 R[] 
    for i in range(0 , n1): 
        L[i] = arr[l + i] 
  
    for j in range(0 , n2): 
        R[j] = arr[m + 1 + j] 
  
    # 归并临时数组到 arr[l..r] 
    i = 0     # 初始化第一个子数组的索引
    j = 0     # 初始化第二个子数组的索引
    k = l     # 初始归并子数组的索引
  
    while i < n1 and j < n2 : 
        if L[i] <= R[j]: 
            arr[k] = L[i] 
            i += 1
        else: 
            arr[k] = R[j] 
            j += 1
        k += 1
  
    # 拷贝 L[] 的保留元素
    while i < n1: 
        arr[k] = L[i] 
        i += 1
        k += 1
  
    # 拷贝 R[] 的保留元素
    while j < n2: 
        arr[k] = R[j] 
        j += 1
        k += 1
  
def mergeSort(arr,l,r): 
    if l < r: 
  
        
        m = int((l+(r-1))/2)
  
       
        mergeSort(arr, l, m) 
        mergeSort(arr, m+1, r) 
        merge(arr, l, m, r) 
  
  
arr = [12, 11, 13, 5, 6, 7] 
n = len(arr) 
print ("给定的数组") 
for i in range(n): 
    print ("%d" %arr[i])
  
mergeSort(arr,0,n-1) 
print ("

排序后的数组") 
for i in range(n): 
    print ("%d" %arr[i])

---------------------------------------------
输出结果：

给定的数组
12
11
13
5
6
7


排序后的数组
5
6
7
11
12
13

4、复杂度

　　时间复杂度：O(nlogn)

　　空间复杂度：O(N)，归并排序需要一个与原数组相同长度的数组做辅助来排序