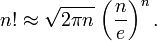题目来源:HDOJ1018(求阶乘的位数)
斯特林公式简介(维基百科):
斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特灵公式十分好用,而且,即使在n很小的时候,斯特灵公式的取值已经十分准确。
公式为:
这就是说,对于足够大的整数n,这两个数互为近似值。

当n增加时,(ln n!)与o (n ln n − n)之比趋于1。
几乎超时:
1 # include <stdio.h>
2 # include <math.h>
3
4 int main()
5 {
6 int T, x, i;
7 double sum;
8
9 scanf("%d", &T);
10 while (T--)
11 {
12 scanf("%d", &x);
13 for (sum=0, i=1; i <= x; ++i)
14 sum += log10(i);
15 printf("%d\n", (int)sum+1);
16 }
17
18 return 0;
19 }
0ms:
1 # include <stdio.h>
2 # include <math.h>
3
4 int main()
5 {
6 int T, n;
7
8 scanf("%d", &T);
9 while (T--)
10 {
11 scanf("%d", &n);
12 printf("%d\n",(int)(n*log10(n/exp(1.0))+0.5*log10(2.0*n*4.0*atan(1.0)))+1);
13 }
14
15 return 0;
16 }