
对于d, 记{ai}中是d的倍数的数的个数为c, 那么有:
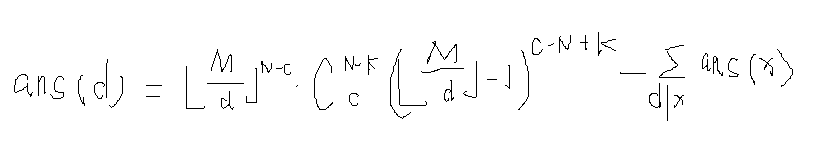
直接计算即可,复杂度O(NlogN+MlogM)
---------------------------------------------------------------------------
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MOD = 1000000007;
const int maxn = 300009;
int ans[maxn];
int N, M, K, seq[maxn], cnt[maxn];
int Inv[maxn], Fac[maxn];
void gcd(int a, int b, int &d, int &x, int &y) {
if(!b) {
d = a;
x = 1;
y = 0;
} else {
gcd(b, a % b, d, y, x);
y -= x * (a / b);
}
}
int INV(int v) {
int d, x, y;
gcd(v, MOD, d, x, y);
return (x + MOD) % MOD;
}
void Init() {
Inv[0] = INV(Fac[0] = 1);
for(int i = 1; i <= N; i++) {
Fac[i] = ll(i) * Fac[i - 1] % MOD;
Inv[i] = INV(Fac[i]);
}
}
int C(int m, int n) {
return ll(Fac[n]) * Inv[n - m] % MOD * Inv[m] % MOD;
}
int Power(int x, int t) {
int ret = 1;
for(; t; t >>= 1, x = ll(x) * x % MOD)
if(t & 1) ret = ll(x) * ret % MOD;
return ret;
}
int main() {
memset(cnt, 0, sizeof cnt);
scanf("%d%d%d", &N, &M, &K);
for(int i = 0; i < N; i++) {
scanf("%d", seq + i);
cnt[seq[i]]++;
}
Init();
for(int i = M; i; i--) {
int c = 0;
for(int j = i; j <= M; j += i)
if(cnt[j]) c += cnt[j];
if(c + K < N) {
ans[i] = 0; continue;
}
ans[i] = (ll) Power(M / i, N - c) * C(N - K, c) % MOD * Power(M / i - 1, c - N + K) % MOD;
for(int j = i << 1; j <= M; j += i)
if((ans[i] -= ans[j]) < 0) ans[i] += MOD;
}
printf("%d", ans[1]);
for(int i = 2; i <= M; i++)
printf(" %d", ans[i]);
return 0;
}
---------------------------------------------------------------------------
4305: 数列的GCD
Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 149 Solved: 68
[Submit][Status][Discuss]
Description
给出一个长度为N的数列{a[n]},1<=a[i]<=M(1<=i<=N)。
现在问题是,对于1到M的每个整数d,有多少个不同的数列b[1], b[2], ..., b[N],满足:
(1)1<=b[i]<=M(1<=i<=N);
(2)gcd(b[1], b[2], ..., b[N])=d;
(3)恰好有K个位置i使得a[i]<>b[i](1<=i<=N)
注:gcd(x1,x2,...,xn)为x1, x2, ..., xn的最大公约数。
输出答案对1,000,000,007取模的值。
Input
第一行包含3个整数,N,M,K。
第二行包含N个整数:a[1], a[2], ..., a[N]。
Output
输出M个整数到一行,第i个整数为当d=i时满足条件的不同数列{b[n]}的数目mod 1,000,000,007的值。
Sample Input
3 3 3
3 3 3
3 3 3
Sample Output
7 1 0
HINT
当d=1,{b[n]}可以为:(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1)。
当d=2,{b[n]}可以为:(2, 2, 2)。
当d=3,因为{b[n]}必须要有k个数与{a[n]}不同,所以{b[n]}不能为(3, 3, 3),满足条件的一个都没有。
对于100%的数据,1<=N,M<=300000, 1<=K<=N, 1<=a[i]<=M。