4873: [Shoi2017]寿司餐厅
Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 450 Solved: 316
[Submit][Status][Discuss]
Description
Kiana最近喜欢到一家非常美味的寿司餐厅用餐。每天晚上,这家餐厅都会按顺序提供n种寿司,第i种寿司有一个
代号ai和美味度di,i,不同种类的寿司有可能使用相同的代号。每种寿司的份数都是无限的,Kiana也可以无限次
取寿司来吃,但每种寿司每次只能取一份,且每次取走的寿司必须是按餐厅提供寿司的顺序连续的一段,即Kiana
可以一次取走第1,2种寿司各一份,也可以一次取走第2,3种寿司各一份,但不可以一次取走第1,3种寿司。由于餐
厅提供的寿司种类繁多,而不同种类的寿司之间相互会有影响:三文鱼寿司和鱿鱼寿司一起吃或许会很棒,但和水
果寿司一起吃就可能会肚子痛。因此,Kiana定义了一个综合美味度di,j(i<j),表示在一次取的寿司中,如果包含
了餐厅提供的从第i份到第j份的所有寿司,吃掉这次取的所有寿司后将获得的额外美味度。由于取寿司需要花费一
些时间,所以我们认为分两次取来的寿司之间相互不会影响。注意在吃一次取的寿司时,不止一个综合美味度会被
累加,比如若Kiana一次取走了第1,2,3种寿司各一份,除了d1,3以外,d1,2,d2,3也会被累加进总美味度中。神奇
的是,Kiana的美食评判标准是有记忆性的,无论是单种寿司的美味度,还是多种寿司组合起来的综合美味度,在
计入Kiana的总美味度时都只会被累加一次。比如,若Kiana某一次取走了第1,2种寿司各一份,另一次取走了第2,3
种寿司各一份,那么这两次取寿司的总美味度为d1,1+d2,2+d3,3+d1,2+d2,3,其中d2,2只会计算一次。奇怪的是,
这家寿司餐厅的收费标准很不同寻常。具体来说,如果Kiana一共吃过了c(c>0)种代号为x的寿司,则她需要为这些
寿司付出mx^2+cx元钱,其中m是餐厅给出的一个常数。现在Kiana想知道,在这家餐厅吃寿司,自己能获得的总美
味度(包括所有吃掉的单种寿司的美味度和所有被累加的综合美味度)减去花费的总钱数的最大值是多少。由于她
不会算,所以希望由你告诉她
Input
第一行包含两个正整数n,m,分别表示这家餐厅提供的寿司总数和计算寿司价格中使用的常数。
第二行包含n个正整数,其中第k个数ak表示第k份寿司的代号。
接下来n行,第i行包含n-i+1个整数,其中第j个数di,i+j-1表示吃掉寿司能
获得的相应的美味度,具体含义见问题描述。
N<=100,Ai<=1000
Output
输出共一行包含一个正整数,表示Kiana能获得的总美味度减去花费的总钱数的最大值。
Sample Input
3 1
2 3 2
5 -10 15
-10 15
15
2 3 2
5 -10 15
-10 15
15
Sample Output
12
【样例1说明】
在这组样例中,餐厅一共提供了3份寿司,它们的代号依次为a1=2,a2=3,a3=2,计算价格时的常数m=1。在保证每
次取寿司都能获得新的美味度的前提下,Kiana一共有14种不同的吃寿司方案:
1.Kiana一个寿司也不吃,这样她获得的总美味度和花费的总钱数都是0,两者相减也是0;
2.Kiana只取1次寿司,且只取第1个寿司,即她取寿司的情况为{[1,1]},这样获得的总美味度为5,花费的总钱数
为1-2^2+1*2=6,两者相减为-1;
3.Kiana只取1次寿司,且只取第2个寿司,即她取寿司的情况为{[2,2]},这样获得的总美味度为-10,花费的总钱
数为1-3^2+1*3=12,两者相减为-22;
4.Kiana只取1次寿司,且只取第3个寿司,即她取寿司的情况为{[3,3]},这样获得的总美味度为15,花费的总钱数
为1*2^2+1*2=6,两者相减为9;
5.Kiana只取1次寿司,且取第1,2个寿司,即她取寿司的情况为{[1,2]},这样获得的总美味度为5+(-10)+(-10)=-1
5,花费的总钱数为(1-2^2+1*2)+(1-3^2+1*3)=18,两者相减为-33;
6.Kiana只取1次寿司,且取第2,3个寿司,即她取寿司的情况为{[2,3]},这样获得的总美味度为(-10)+15+15=20,
花费的总钱数为(1-2^2+1*2)+(1*3^2+1*3)=18,两者相减为2;
7.Kiana只取1次寿司,且取第1,2,3个寿司,即她取寿司的情况为{[1,3]},这样获得的总美味度为5+(-10)+15+(-1
0)+15+15=30,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减为10。
8.Kiana取2次寿司,第一次取第1个寿司,第二次取第2个寿司,即她取寿司的情况为{[1,1],[2,2]},这样获得的
总美味度为5+(-10)=-5,花费的总钱数为(1*2^2+1*2)+(1*3^2+1*3)=18,两者相减为-23;
9.Kiana取2次寿司,第一次取第1个寿司,第二次取第3个寿司,即她取寿司的情况为{[1,1],[3,3]},这样获得的
总美味度为5+15=20,花费的总钱数为1*2^2+2*2=8,两者相减为12;
10.Kiana取2次寿司,第一次取第2个寿司,第二次取第3个寿司,即她取寿司的情况为{[2,2],[3,3]},这样获得的
总美味度为(-10)+15=5,花费的总钱数为(1*2^2+1*2)+(1*3^2+1*3)=18,两者相减为-13;
11.Kiana取2次寿司,第一次取第1,2个寿司,第二次取第3个寿司,即她取寿司的情况为{[1,2],[3,3]},这样获得
的总美味度为5+(-10)+(-10)+15=0,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减为-20;
12.Kiana取2次寿司,第一次取第1个寿司,第二次取第2,3个寿司,即她取寿司的情况为{[1,1],[2,3]},这样获得
的总美味度为5+(-10)+15+15=25,花费的总钱数为(1-22+2-2)+(1-32+1-3)=20,两者相减为5;
13.Kiana取2次寿司,第一次取第1,2个寿司,第二次取第2,3个寿司,即她取寿司的情况为{[1,2],[2,3]},这样获
得的总美味度为5+(-10)+15+(-10)+15=15,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减为-5;
14.Kiana取3次寿司,第一次取第1个寿司,第二次取第2个寿司,第三次取第3个寿司,即她取寿司的情况为{[1,1]
,[2,2],[3,3]},这样获得的总美味度为5+(-10)+15=10,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减
为-10。
所以Kiana会选择方案9,这时她获得的总美味度减去花费的总钱数的值最大为12。
【样例1说明】
在这组样例中,餐厅一共提供了3份寿司,它们的代号依次为a1=2,a2=3,a3=2,计算价格时的常数m=1。在保证每
次取寿司都能获得新的美味度的前提下,Kiana一共有14种不同的吃寿司方案:
1.Kiana一个寿司也不吃,这样她获得的总美味度和花费的总钱数都是0,两者相减也是0;
2.Kiana只取1次寿司,且只取第1个寿司,即她取寿司的情况为{[1,1]},这样获得的总美味度为5,花费的总钱数
为1-2^2+1*2=6,两者相减为-1;
3.Kiana只取1次寿司,且只取第2个寿司,即她取寿司的情况为{[2,2]},这样获得的总美味度为-10,花费的总钱
数为1-3^2+1*3=12,两者相减为-22;
4.Kiana只取1次寿司,且只取第3个寿司,即她取寿司的情况为{[3,3]},这样获得的总美味度为15,花费的总钱数
为1*2^2+1*2=6,两者相减为9;
5.Kiana只取1次寿司,且取第1,2个寿司,即她取寿司的情况为{[1,2]},这样获得的总美味度为5+(-10)+(-10)=-1
5,花费的总钱数为(1-2^2+1*2)+(1-3^2+1*3)=18,两者相减为-33;
6.Kiana只取1次寿司,且取第2,3个寿司,即她取寿司的情况为{[2,3]},这样获得的总美味度为(-10)+15+15=20,
花费的总钱数为(1-2^2+1*2)+(1*3^2+1*3)=18,两者相减为2;
7.Kiana只取1次寿司,且取第1,2,3个寿司,即她取寿司的情况为{[1,3]},这样获得的总美味度为5+(-10)+15+(-1
0)+15+15=30,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减为10。
8.Kiana取2次寿司,第一次取第1个寿司,第二次取第2个寿司,即她取寿司的情况为{[1,1],[2,2]},这样获得的
总美味度为5+(-10)=-5,花费的总钱数为(1*2^2+1*2)+(1*3^2+1*3)=18,两者相减为-23;
9.Kiana取2次寿司,第一次取第1个寿司,第二次取第3个寿司,即她取寿司的情况为{[1,1],[3,3]},这样获得的
总美味度为5+15=20,花费的总钱数为1*2^2+2*2=8,两者相减为12;
10.Kiana取2次寿司,第一次取第2个寿司,第二次取第3个寿司,即她取寿司的情况为{[2,2],[3,3]},这样获得的
总美味度为(-10)+15=5,花费的总钱数为(1*2^2+1*2)+(1*3^2+1*3)=18,两者相减为-13;
11.Kiana取2次寿司,第一次取第1,2个寿司,第二次取第3个寿司,即她取寿司的情况为{[1,2],[3,3]},这样获得
的总美味度为5+(-10)+(-10)+15=0,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减为-20;
12.Kiana取2次寿司,第一次取第1个寿司,第二次取第2,3个寿司,即她取寿司的情况为{[1,1],[2,3]},这样获得
的总美味度为5+(-10)+15+15=25,花费的总钱数为(1-22+2-2)+(1-32+1-3)=20,两者相减为5;
13.Kiana取2次寿司,第一次取第1,2个寿司,第二次取第2,3个寿司,即她取寿司的情况为{[1,2],[2,3]},这样获
得的总美味度为5+(-10)+15+(-10)+15=15,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减为-5;
14.Kiana取3次寿司,第一次取第1个寿司,第二次取第2个寿司,第三次取第3个寿司,即她取寿司的情况为{[1,1]
,[2,2],[3,3]},这样获得的总美味度为5+(-10)+15=10,花费的总钱数为(1*2^2+2*2)+(1*3^2+1*3)=20,两者相减
为-10。
所以Kiana会选择方案9,这时她获得的总美味度减去花费的总钱数的值最大为12。
HINT
Source
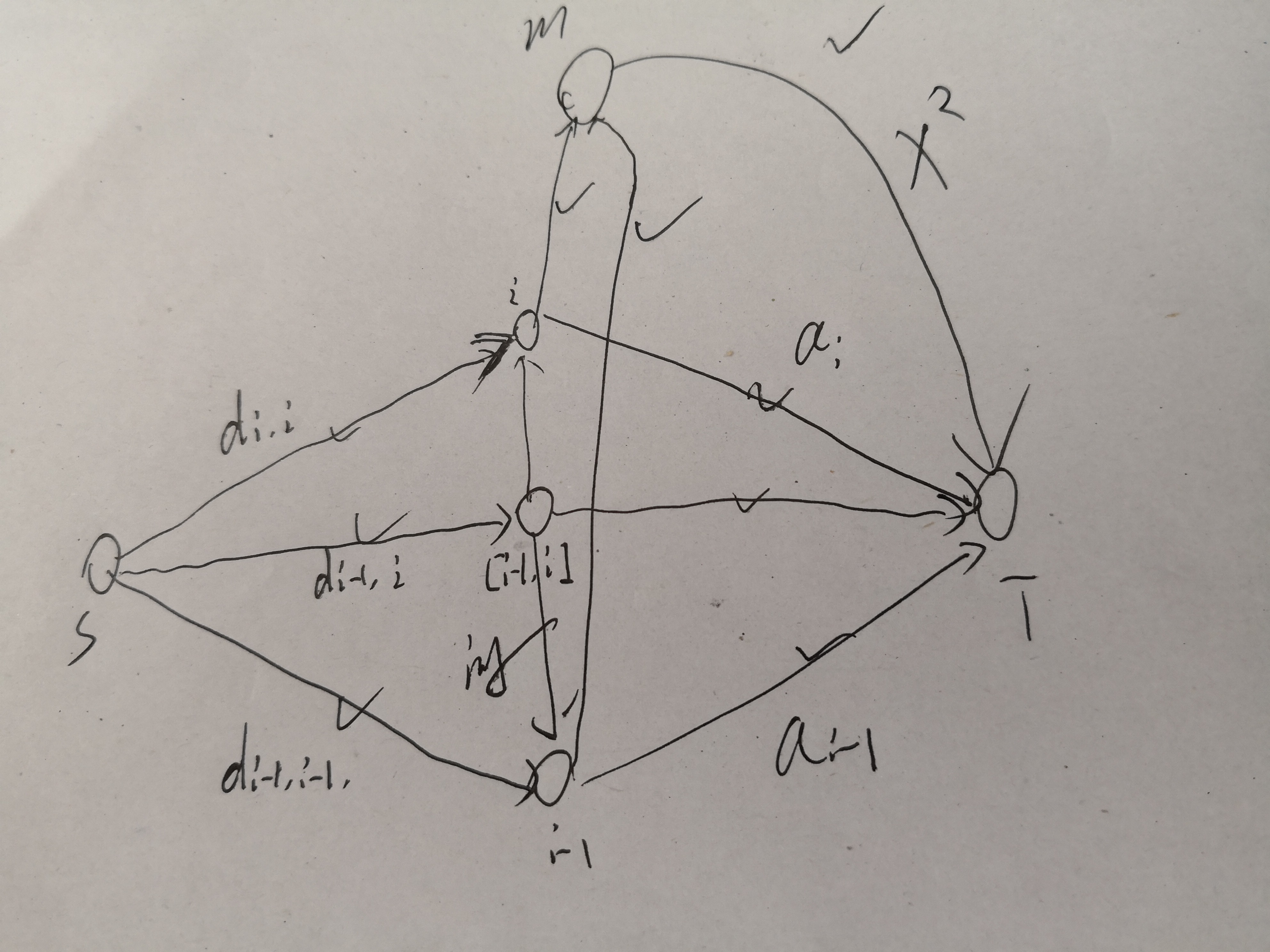
每个区间可以选或者不选,区间之间还有限制,一下子想到集合划分。
可以考虑下图
#include<bits/stdc++.h>
#define ll long long
#define maxn 20005
#define pb push_back
using namespace std;
const int inf=1<<30;
vector<int> g[maxn];
struct lines{
int to,flow,cap;
}l[maxn*10];
int S,T,t=-1,d[maxn],cur[maxn];
bool v[maxn];
inline void add(int from,int to,int cap){
l[++t]=(lines){to,0,cap},g[from].pb(t);
l[++t]=(lines){from,0,0},g[to].pb(t);
}
inline bool BFS(){
memset(v,0,sizeof(v));
queue<int> q;
q.push(S),v[S]=1,d[S]=0;
int x; lines e;
while(!q.empty()){
x=q.front(),q.pop();
for(int i=g[x].size()-1;i>=0;i--){
e=l[g[x][i]];
if(e.flow<e.cap&&!v[e.to]){
v[e.to]=1,d[e.to]=d[x]+1;
q.push(e.to);
}
}
}
return v[T];
}
int dfs(int x,int a){
if(!a||x==T) return a;
int flow=0,f,sz=g[x].size();
for(int &i=cur[x];i<sz;i++){
lines &e=l[g[x][i]];
if(d[e.to]==d[x]+1&&(f=dfs(e.to,min(a,e.cap-e.flow)))){
a-=f,flow+=f;
e.flow+=f,l[g[x][i]^1].flow-=f;
if(!a) break;
}
}
return flow;
}
inline int max_flow(){
int an=0;
while(BFS()){
memset(cur,0,sizeof(cur));
an+=dfs(S,1<<30);
}
return an;
}
int n,m,D[105][105],cnt=1000;
int a[105],id[105][105],tt=0;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",a+i);
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++){
scanf("%d",&D[i][j]);
id[i][j]=++cnt;
}
S=0,T=cnt+1;
if(m) for(int i=1;i<=1000;i++) add(i,T,i*i);
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++){
if(i==j) add(id[i][j],a[i],inf),add(id[i][j],T,a[i]);
else add(id[i][j],id[i+1][j],inf),add(id[i][j],id[i][j-1],inf);
if(D[i][j]>0) add(S,id[i][j],D[i][j]),tt+=D[i][j];
else add(id[i][j],T,-D[i][j]);
}
printf("%d
",tt-max_flow());
return 0;
}