题目描述
菲菲和牛牛在一块n 行m 列的棋盘上下棋,菲菲执黑棋先手,牛牛执白棋后手。 棋局开始时,棋盘上没有任何棋子,两人轮流在格子上落子,直到填满棋盘时结束。
落子的规则是:一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。
棋盘的每个格子上,都写有两个非负整数,从上到下第i 行中从左到右第j 列的格 子上的两个整数记作A_{i,j}Ai,j 、B_{i,j}Bi,j 。在游戏结束后,菲菲和牛牛会分别计算自己的得分:菲菲的得分是所有有黑棋的格子上的A_{i,j}Ai,j 之和,牛牛的得分是所有有白棋的格子上的B_{i,j}Bi,j 的和。
菲菲和牛牛都希望,自己的得分减去对方的得分得到的结果最大。现在他们想知道,在给定的棋盘上,如果双方都采用最优策略且知道对方会采用最优策略,那么,最终的结果如何。
输入输出格式
输入格式:
从文件chess.in 中读入数据。
输入第一行包含两个正整数n;m,保证n;m <= 10。
接下来n 行,每行m 个非负整数,按从上到下从左到右的顺序描述每个格子上的 第一个非负整数:其中第i 行中第j 个数表示A_{i,j}Ai,j 。
接下来n 行,每行m 个非负整数,按从上到下从左到右的顺序描述每个格子上的 第二个非负整数:其中第i 行中第j 个数表示B_{i,j}Bi,j 。
输出格式:
输出到文件chess.out 中。
输出一个整数,表示菲菲的得分减去牛牛的得分的结果。
输入输出样例
说明
样例1说明:
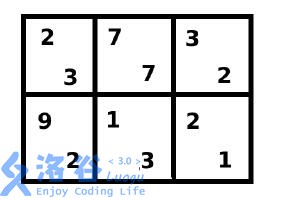
棋盘如图所示,双方都采用最优策略时,棋局如下:
• 菲菲下在第1 行第1 列(这是第一步时唯一可以落子的格子);
• 牛牛下在第1 行第2 列;
• 菲菲下在第2 行第1 列;
• 牛牛下在第1 行第3 列;
• 菲菲下在第2 行第2 列;
• 牛牛下在第2 行第3 列(这是这一步时唯一可以落子的格子);
• 填满棋盘,游戏结束,盘面如下。
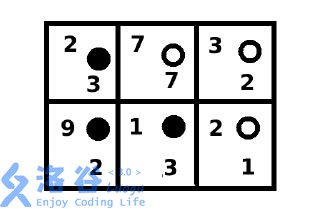
菲菲的得分为:2 + 9 + 1 = 12 ;牛牛的得分为:7 + 2 + 1 = 10 。
对于所有的测试数据,n;m <= 10 ,A_{i,j}Ai,j ; B_{i,j}Bi,j <= 100000。
对于编号为奇数的测试点,保证所有的B_{i,j}Bi,j = 0 。
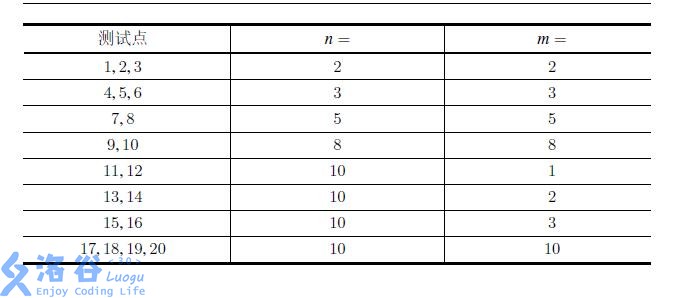
可以把每列选的前多少行作为状态,这样做之后发现总状态数最多就是 C(20,10) ,就是考虑 从左下角只能向右向上走到右上角的方案数。
然后直接反着状压dp就可以直接做啦。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#include<map>
#define ll long long
using namespace std;
const int inf=1e9;
int n,m,a[105][105],b[105][105];
int num=0,f[1000005];
ll P[1000005];
map<ll,int> mmp;
void dfs(int x,int y,ll tot){
if(!x){
P[++num]=tot,mmp[tot]=num;
return;
}
for(int i=y;i<=n;i++) dfs(x-1,i,tot*11ll+(ll)i);
}
inline void dp(){
f[num]=0;
for(int i=num-1;i;i--){
ll O=P[i],U=P[i],B=1;
if(!(P[i]&1)){
f[i]=-inf;
for(int j=1,lef,to;j<=m;j++,B*=11ll,U/=11) if((lef=U%11)<n){
to=mmp[O+B];
if(to) f[i]=max(f[i],f[to]+a[lef+1][j]);
}
}
else{
f[i]=inf;
for(int j=1,lef,to;j<=m;j++,B*=11ll,U/=11) if((lef=U%11)<n){
to=mmp[O+B];
if(to) f[i]=min(f[i],f[to]-b[lef+1][j]);
}
}
}
}
int main(){
// freopen("chess.in","r",stdin);
// freopen("chess.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%d",&b[i][j]);
dfs(m,0,0);
dp();
printf("%d
",f[1]);
return 0;
}