
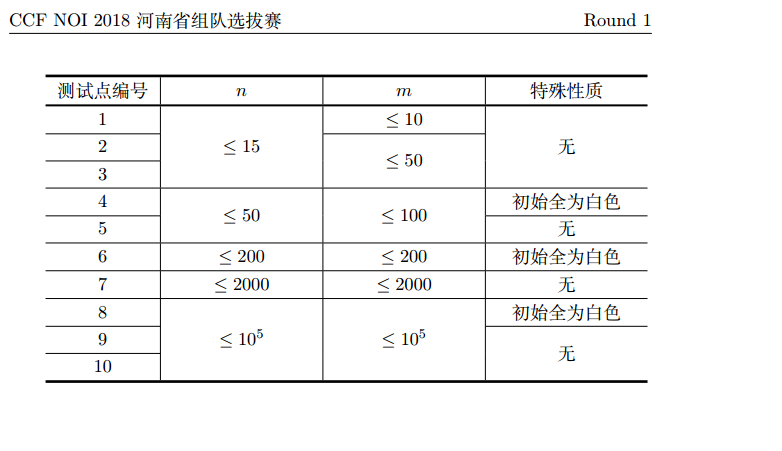
做法超好想,细节调一辈子。 估计这句话最适合这个题了hhhh。
首先一个很显然的想法:把边设成未知数,对点列异或方程,最后的解的个数就是 2^自由元 。
不过如果某个联通分量里有奇数个黑点,那么问题无解。然后我来证明一下:
把一个联通分量里所有点代表的方程都异或起来,因为这个联通分量里的边恰好在其两个端点的行是1,所以最后异或出来的方程前m列都是0,如果有奇数个黑点的话,最后一列就是1,那么无解(不能0=1吧hhh)。
直接高斯消元是 O(N^3) 的,肯定要gg了啊 (不过竟然给了60分消元hhh,出题人太良心了)。
不过一般这种题我们如果按照特定的顺序消(shou)元(wan)的话,会得到一些很良心的结论(具体参考 bzoj 文艺计算姬)。
考虑 边1 的两个端点 u,v,因为最后只能有一行对应在这列是1,所以我们就把第v行变成 第u行 异或 第v行,可以发现得到的新行的意义是:u点和v点合并后的新点(因为边1被消去了,正好对应一个点没有自环)。
当然,如果我们考虑边i的时候,发现它的两个端点已经在一个联通分量里了,那么这条边就是自由元,因为我们现在在高斯消元的矩阵里已经找不到第i列是1的行了。
我们把上述做法扩展一下,就可以得到一个能够算出全局答案的做法:初始答案是1,并查集维护连通性,如果尝试合并失败,那么答案*2。
但是这还不够棒,因为本题要求出 删去 每一个点之后的答案。
不过上述做法还是有点多余,因为我们仔细想一下它的过程,就可以发现其实答案就是 2^(m-n + 联通分量个数)。
所以,现在我们还剩下的最大的问题就是:如何维护,删去一个点之后,可能带来的某个联通分量的黑点变成奇数个(对应无解) 和 联通分量个数的变动 (对应图的连通性) 的影响???
跑个tarjan求割点的算法就好啦,第一个问题有些复杂,我们先解决一下第二个问题。
第二个问题无非可以分以下几种情况:
1.删去的节点是一个孤立顶点: 这种情况下 会使图中联通分量个数-1.
2.删去一个割点: 这种情况可以在tarjan的时候顺带统计,不过如果这个点是dfs树的根的话答案还要再-1(因为上面就没有新的联通分量了)
3.删去一个非孤立顶点且非割点:没有影响hhhh。
但是不要忘了,删一个点的时候不仅会对联通分量个数产生影响,还会对图的总边数-点数 产生影响。
至于第一个问题,我们可以在tarjan的时候处理出:删去一个点之后,图中 有奇数个黑点的联通分量 的个数的 变化量 derta[i]。
怎么处理呢?
首先如果这个点是割点的话:
1.如果这个点在的联通分量本来就有 奇数个黑点 的话,那么先让 derta[i]-- ,因为删去这个点会破坏这个联通分量。
2.再让derta[i]加上 删去这个点之后, 在dfs树上不能回到祖先的有奇数个黑点的联通分量个数 。
3.如果 dfs树根所在的联通分量在删去这个点之后也有奇数个黑点,那么 derta[i]++。
如果这个点i是非割点且非孤立顶点的话,那么derta[i] = color[i] == 1 ? (color[this tree] == 1 ? -1 : 1) : 0 .
如果这个点是孤立顶点的话,那么derta[i] = color[i] == 1 ? -1 : 0.
(呼。。。。。终于写完了累死我了。。。。)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=200005,ha=1000000007;
inline int add(int x,int y){ x+=y; return x>=ha?x-ha:x;}
int to[maxn*2],ne[maxn*2],hd[maxn],num,n,m,T,ans,Sub[maxn];
int Xor[maxn],NewC[maxn],NewB[maxn],BC,ci[maxn];
int dfn[maxn],low[maxn],dc,tp,st[maxn],D[maxn];
bool iscut[maxn];
char S[maxn];
inline void addline(int x,int y){ to[++num]=y,ne[num]=hd[x],hd[x]=num,D[x]++;}
inline void init(){
memset(hd,0,sizeof(hd)),num=0;
memset(NewB,0,sizeof(NewB));
memset(NewC,0,sizeof(NewC));
memset(D,0,sizeof(D));
memset(iscut,0,sizeof(iscut));
memset(dfn,0,sizeof(dfn));
memset(Sub,0,sizeof(Sub));
dc=BC=0;
}
inline int read(){
int x=0; char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x;
}
void W(int x){ if(x>=10) W(x/10); putchar(x%10+'0');}
void dfs(int x,int fa){
st[++tp]=x,dfn[x]=low[x]=++dc;
int cd=0; Sub[x]=Xor[x];
for(int i=hd[x];i;i=ne[i]) if(to[i]!=fa)
if(!dfn[to[i]]){
cd++,dfs(to[i],x);
Xor[x]^=Xor[to[i]];
low[x]=min(low[x],low[to[i]]);
if(low[to[i]]>=dfn[x]){
Sub[x]^=Xor[to[i]];
iscut[x]=1,NewC[x]++;
if(Xor[to[i]]) NewB[x]++;
}
}
else low[x]=min(low[x],dfn[to[i]]);
if(cd==1&&fa<0) iscut[x]=NewB[x]=NewC[x]=0;
else if(fa<0) NewC[x]--;
}
inline void solve(){
for(int i=1;i<=n;i++) if(S[i]=='1') Xor[i]=1; else Xor[i]=0;
ans=m-n;
for(int i=1;i<=n;i++) if(!dfn[i]){
ans++;
dfs(i,-1);
if(Xor[i]) BC++;
if(!hd[i]) NewC[i]=-1;
for(;tp;tp--) if(iscut[st[tp]]){
if(Xor[i]^Sub[st[tp]]) NewB[st[tp]]++;
if(Xor[i]==1) NewB[st[tp]]--;
}
else NewB[st[tp]]=S[st[tp]]=='1'?(Xor[i]?-1:1):0;
}
if(BC) W(0); else W(ci[ans]); putchar(' ');
for(int i=1;i<=n;i++){
BC+=NewB[i],ans+=NewC[i]-D[i]+1;
if(!BC) W(ci[ans]); else W(0); putchar(' ');
BC-=NewB[i],ans-=NewC[i]-D[i]+1;
}
puts("");
}
int main(){
ci[0]=1; for(int i=1;i<=200000;i++) ci[i]=add(ci[i-1],ci[i-1]);
T=read();
while(T--){
int uu,vv;
init(),n=read(),m=read();
for(int i=1;i<=m;i++) uu=read(),vv=read(),addline(uu,vv),addline(vv,uu);
scanf("%s",S+1),solve();
}
return 0;
}