「CTSC2018」假面

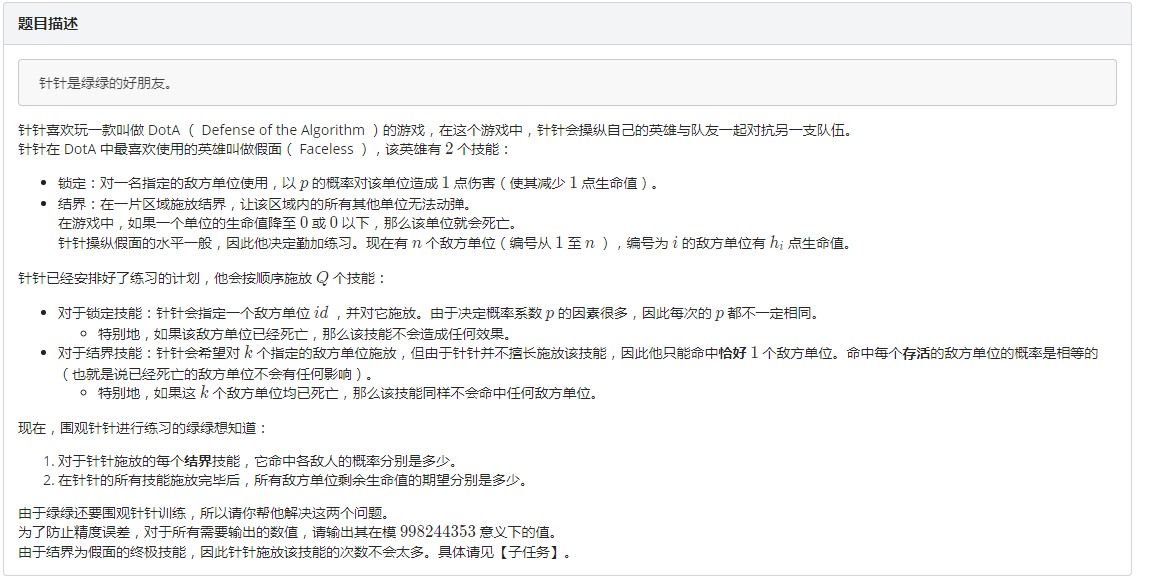
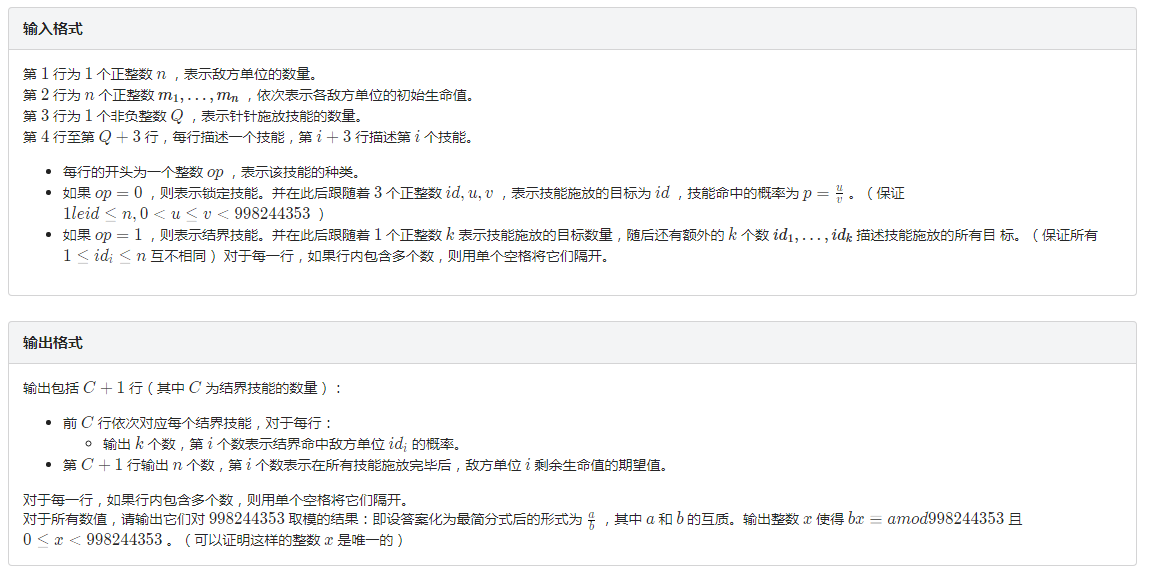
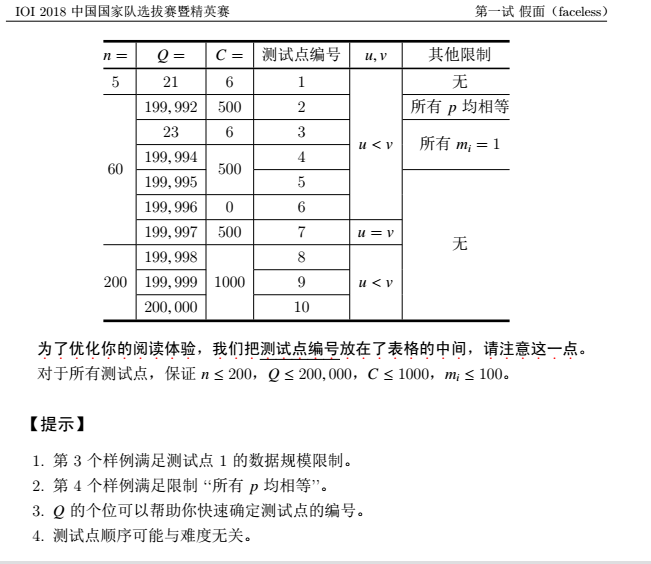
    真~签到题qwq

    昨天在考场上先写了个70分暴力dp，然后发现好像可以优化。因为结界技能的模型相当于要求出 对于每个物品，仅仅不选它的背包是什么。。。。  于是当场脑补出两种做法： 前缀和后缀背包卷积NTT、以及单点删除背包的分治做法。

    想了想两种做法都是 O(N^2 log N) 的，并且NTT我更有把握一点(写得多不太容易gg)，所以果断写了NTT。。。

    复测完之后，带log的只有NTT被卡成暴力分gg,其他的分治做法的都被放过去了qwq（虽然正解没log）。

    艹NTT的log大的上天，我以后再也不写了mmp！！！

    正解是这样的：仔细想想不难发现，这个背包删除物品其实可以做到 O(N)，逆着退一下就好了hhhhhh。

GG

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int ha=998244353,maxn=205;
int F[maxn][105],f[maxn],g[maxn],tp[maxn];
int n,m,u,v,ni[maxn],op,num,now,P[maxn],Q;
inline int add(int x,int y){ x+=y; return x>=ha?x-ha:x;}
inline int ksm(int x,int y){ int an=1; for(;y;y>>=1,x=x*(ll)x%ha) if(y&1) an=an*(ll)x%ha; return an;}

inline void update(int *a,int x){
	a[0]=add(a[0],a[1]*(ll)u%ha);
	for(int i=1;i<=tp[x];i++) a[i]=add(a[i]*(ll)v%ha,a[i+1]*(ll)u%ha);
}

inline void output(){
	for(int i=1,ans;i<=n;i++){
		ans=0;
		for(int j=1;j<=tp[i];j++) ans=add(ans,F[i][j]*(ll)j%ha);
		printf("%d ",ans);
	}
}

inline void calc(){
	memset(f,0,sizeof(f));
	
	f[0]=1;
	for(int i=1;i<=num;i++){
		v=F[P[i]][0],u=add(1,ha-v);
		for(int j=i;j>=0;j--) f[j]=add(f[j]*(ll)v%ha,j?f[j-1]*(ll)u%ha:0);
	}
	
	for(int i=1,ans,iv,iu;i<=num;i++){
		v=F[P[i]][0],u=add(1,ha-v),ans=0;
		iv=ksm(v,ha-2),iu=ksm(u,ha-2);
		
		if(v){
		    g[0]=f[0]*(ll)iv%ha;
		    for(int j=1;j<num;j++) g[j]=add(f[j],ha-g[j-1]*(ll)u%ha)*(ll)iv%ha;
        }
        else for(int j=0;j<num;j++) g[j]=f[j+1];
        
		for(int j=0;j<num;j++) ans=add(ans,ni[j+1]*(ll)g[j]%ha);
		printf("%d ",ans*(ll)u%ha);
	}
	
	puts("");
}

inline void solve(){
	scanf("%d",&Q);
	while(Q--){
		scanf("%d",&op);
		if(!op){
			scanf("%d%d%d",&now,&u,&v);
			u=u*(ll)ksm(v,ha-2)%ha,v=add(1,ha-u);
			update(F[now],now);
		}
		else{
			scanf("%d",&num);
			for(int i=1;i<=num;i++) scanf("%d",P+i);
			calc();
		}
	}
	
	output();
}

int main(){
	ni[1]=1;
	for(int i=2;i<=201;i++) ni[i]=-ni[ha%i]*(ll)(ha/i)%ha+ha;
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&now),F[i][now]=1,tp[i]=now;
	solve();
	return 0;
}