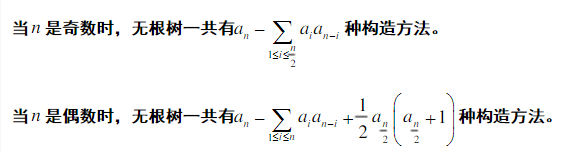先安利一发。让我秒懂。。
第一次讲这个是在寒假。。。然而当时秦神太巨了导致我这个蒟蒻自闭+颓废。。。早就忘了这个东西了。。。
结果今天老师留的题中有两道这种的:Luogu P4981 P4430
然后决定了解一下。。。
一.Prufer序列
Prufer序列,可以用来解一些关于无根树计数的问题。
Prufer序列是一种无根树的编码表示,对于一棵n个节点带编号的无根树,对应唯一一串长度为n-1的Prufer编码,这性质很好。
1.无根树转化为Prufer序列
首先定义无根树中度数为1的节点是叶子节点(显然)
找到编号最小的叶节点,删除这个节点,然后与这个叶节点相连的点计入序列,直到这棵树只剩下两个节点,一条边
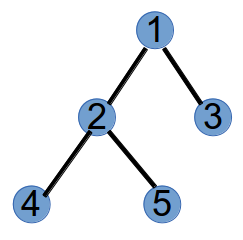
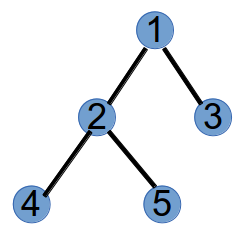
如下图的树对应的Prufer序列就是3,5,1,3
具体实现可以用一个set搞定,维护度数为1的节点。复杂度O(nlogn)。
2.Prufer序列转化为无根树。
设点集V={1,2,3,...,n},每次取出Prufer序列中最前面的元素u,在V中找到编号最小的没有在Prufer序列中出现的元素v,给u,v连边然后从序列中删除v,最后在V中剩下两个节点,给它们连边。最终得到的就是无根树。
具体实现也可以用一个set,维护Prufer序列中没有出现的编号。复杂度O(nlogn)。
最后有一个很重要的性质就是Prufer序列中某个编号出现的次数就等于这个编号的节点在无根树中的度数-1。
还如果不清楚,看下面(以下引用来自朝拜明天19891101)
第一部分:树编码成Prufer序列。
树编码成Prufer序列的方式是:Prufer序列初始为空。每次从树上选出一个编号最小的叶子节点,然后将与该叶子节点相邻的那个节点的编号写入Prufer序列的末尾,之后从树上删掉这个叶子节点。循环这个步骤n-2次,最后得到一个长度为n-2的Prufer序列(此时树中只有一条边,我们就不管它了)。
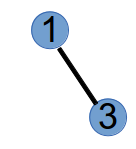
我们以下面这个树为例。
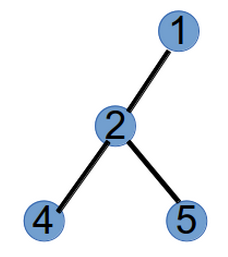
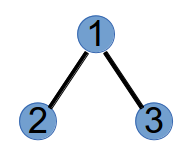
step1:编号最小的叶子节点为3,将与其相连的节点1加到Prufer的末尾,并将3从树上删掉,此时Prufer序列为(1),树变为如下:step2:编号最小的叶子节点为1,将与其相连的节点2加到Prufer末尾,此时Prufer序列为(1,2),并将节点1删掉,树变为如下:
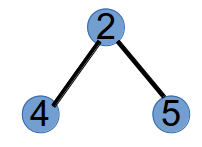
step3:编号最小的叶子节点为4,将与其相连的节点2加入到Prufer的末尾,此时Prufer序列为(1,2,2),并将节点4删掉,树变为如下:
此时,结束,我们得到了Prufer序列为(1,2,2)。
第二部分:由Prufer序列得到树。首先,将每个节点的度数设为1加上该节点在Prufer序列中出现的次数。然后以下循环执行n-2次。第i次循环,选择此时度数为1的编号最小的节点u,将其与此时Prufer序列的第i个元素v连边,然后将u和v的度数都减去1。这n-2次执行完之后,仅剩下两个节点他们的度数都是1,将这两个点连边,这样就得到一个有n-1条边的树。
下面,我们以上面的Prufer序列为例还原这个树。初始的Prufer为(1,2,2),初始的度数为:
step1:选择度数为1的最小编号的节点3与Prufer的第一个元素1连边,并将3和1的度数都减去1,得到树和新的度数:
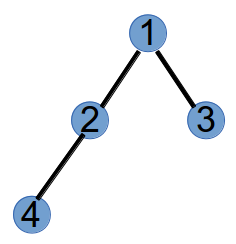
step2:选择度数为1的最小节点1和Prufer中的第二个元素2连边,并将1和2的度数都减去1,得到树和新的度数:
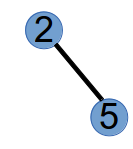
step3:选择度数为1的最小节点4和Prufer中的第三个元素2连边,并将4和2的度数都减去1,得到树和新的度数:
最后,将仅有的度数为1的两个节点2和5,连边,得到:
那么,我们知道这些有什么用呢?看下面
二.Cayley公式
Cayley公式是说,一个无向完全图有n^(n-2)棵生成树,通俗的说就是n个节点的带编号的无根树有n^(n-2)个。
刚才Prufer有一个很重要的性质:序列与树是一一对应的
而Prufer序列有n-2项,序列中的每个数都在1到n的范围内。
所以我们可以直接推出n个点的无向完全图的生成树的计数:n^(n-2)
一个有趣的推广是,n个节点的度依次为D1, D2, …, Dn的无根树共有 (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ] 个,因为此时Prüfer编码中的数字i恰好出现Di-1次(上面的结论)。
下面的结论都看不懂,先咕着:(链接)
3)n个节点的度依次为D1, D2, …, Dn,令有m个节点度数未知,求有多少种生成树?(BZOJ1005 明明的烦恼)
令每个已知度数的节点的度数为di,有n个节点,m个节点未知度数,left=(n-2)-(d1-1)-(d2-1)-...-(dk-1)
已知度数的节点可能的组合方式如下
(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left!
剩余left个位置由未知度数的节点随意填补,方案数为m^left
于是最后有
ans=(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left! * m^left
待填之坑:无标号无根树、有标号有根树、无标号有根树的计数。
参见论文 华中师大一附中 赵爽《树的计数》、南京师范大学附属中学 顾昱洲《Graphical Enumeration》
n个点的 有标号有根树的计数:n^(n-2)*n = n^(n-1)
n个点的 无标号有根树的计数:
n个点的 无标号无根树的计数:an为 n个点的 无标号有根树的计数。
待填之坑:度数有限制时的计数。如烷烃的计数,每个点的度数最大为4。
2019.05.06