Luogu P4478 [BJWC2018]上学路线 卢卡斯+组合+CRT

首先，从$(0,0)$走到$(n,m)$的方案数是$ C_{n+m}^n$，可以把走的方向看作一种序列，这个序列长$ n+m$ ，你需要从中任取$n$个位置，让他向右走；

然后就是如何处理不能走的点：把点sort一遍，按横纵坐标降序排列，这样前面的点可能会包含后面的点，所以算方案数时时要考虑。

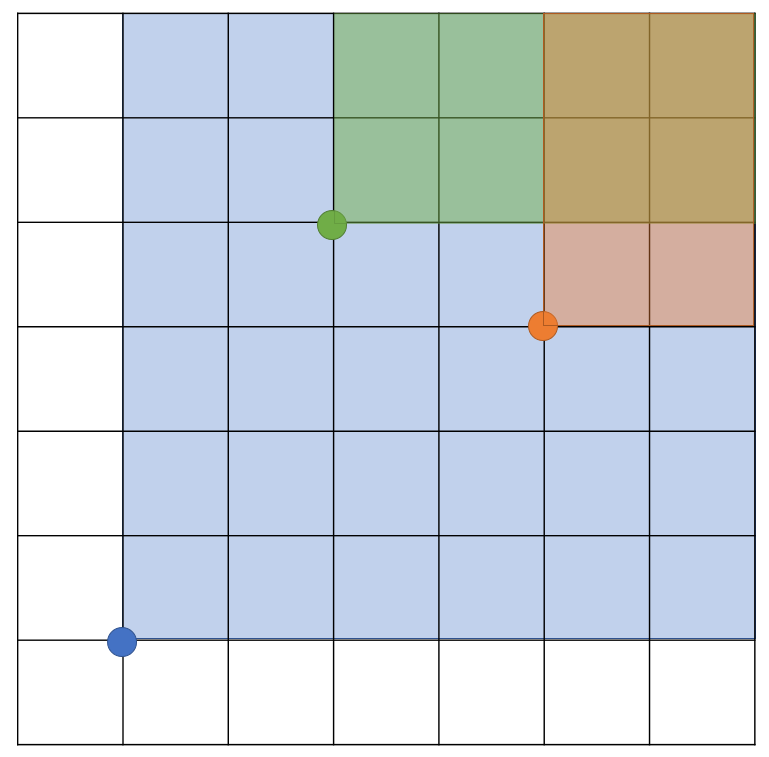
算出来从$(0,0)$到$橙色的点(x,y)$的方案数为$C_{x+y}^x$，再减去蓝色点*蓝色点到橙色点方案数，才是到橙色点的方案数；

注意每条非法路径只会被第一个经过他的非法的点记录。

在最后把每个店的方案数再乘上到终点的代价，就是在模其中一个数意义下的解；

最最后用中国剩余定理合并。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define ll long long 
#define R register ll
using namespace std;
inline ll g() {
    R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix;
    do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix;
}
struct node {int x,y;
    bool operator <(const node& b) const{return x==b.x?y<b.y:x<b.x;}
} a[210];
ll f[210],p[5],ans[5],M[5],T[5];
ll fac[1000010],inv[1000010];
inline ll C(ll n,ll m,ll p) {
    if(n<m) return 0; return fac[n]*inv[fac[m]*fac[n-m]%p]%p;
}
inline ll L(ll n,ll m,ll p) {
    if(n<m) return 0; if(!n) return 1;
    return L(n/p,m/p,p)*C(n%p,m%p,p)%p;
}
ll n,m,t,mod,tot,S=1;
signed main() {
    n=g(),m=g(),t=g(),mod=g();
    if(mod==1000003) p[++tot]=mod;
    else p[1]=3,p[2]=5,p[3]=6793,p[4]=10007,tot=4;
    for(R i=1;i<=t;++i) a[i].x=g(),a[i].y=g();
    sort(a+1,a+t+1); for(R i=1;i<=tot;++i) S*=p[i]; 
    for(R i=1;i<=tot;++i) M[i]=S/p[i]; inv[1]=1,fac[0]=1;
    for(R k=1;k<=tot;++k) {
        R P=p[k]; for(R i=2;i<P;++i) inv[i]=(P-P/i*inv[P%i]%P)%P;
        T[k]=inv[M[k]%P]; for(R i=1;i<P;++i) fac[i]=fac[i-1]*i%P;
        ans[k]=L(n+m,n,P); for(R i=1;i<=t;++i) {
            f[i]=L(a[i].x+a[i].y,a[i].x,P);
            for(R j=1;j<i;++j) if(a[j].x<=a[i].x&&a[j].y<=a[i].y) 
                f[i]+=(P-f[j]*L(a[i].x+a[i].y-a[j].x-a[j].y,a[i].x-a[j].x,P)%P)%P;
            f[i]%=P; ans[k]+=P-L(n+m-a[i].x-a[i].y,n-a[i].x,P)*f[i]%P;
        } ans[k]%=P;
    } ll anss=0; for(R i=1;i<=tot;++i) anss+=ans[i]*M[i]%mod*T[i]%mod;
    printf("%lld
",anss%mod);
} 

---

2019.05.18