BZOJ 4892 [Tjoi2017]dna 哈希+二分

自己简直是傻死了。。。对于位置想错了。。。

---

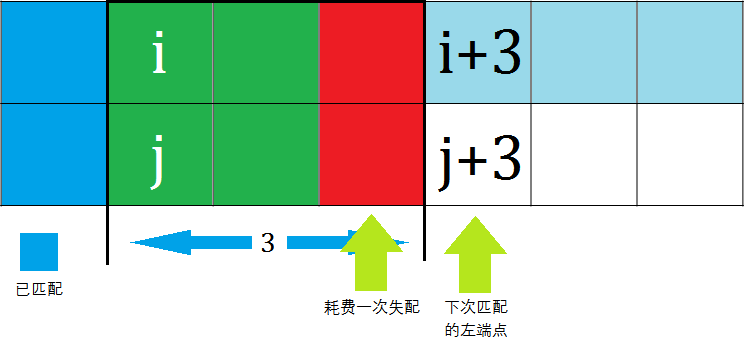
二分出来的是LCP长度$+1$，即每一次二分出来的最后一个点都是失配的，而就算失配也会跳过这个点；所以当$k<=3$且模式串$s2$的指针$>len2$时，即跳过了$<=3$个点的位置且指针$>len2$时，都是可行的；当$k==4$且模式串$s2$指针$>len2+1$时，即跳过了$<=4$个点的位置$>len2+1$时，是可行的。注意到时$len2+1$，原因是多失配了一个四号点。

然后一晚上又过去了$qwq$

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<vector>
#include<queue>
#include<map>
#include<set>
#define ll unsigned long long
#define R register int
using namespace std;
namespace Fread {
    //static char B[1<<15],*S=B,*D=B;
    //#define getchar() (S==D&&(D=(S=B)+fread(B,1,1<<15,stdin),S==D)?EOF:*S++)
    inline int g() {
        R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix;
        do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix;
    }
}using Fread::g;
const int N=100010,B=131;
ll h1[N],h2[N],p[N]; int n,l1,l2,t;
char s1[N],s2[N];
inline ll H1(int l,int r) {return h1[r]-h1[l-1]*p[r-l+1];}
inline ll H2(int l,int r) {return h2[r]-h2[l-1]*p[r-l+1];}
inline int ck(int x) {
    R i=x,j=1; R l=0,r=l2+1;
    for(R k=1;k<=4;++k) {
        while(l<r) { R md=l+r>>1; 
            if(H1(i,i+md-1)==H2(j,j+md-1)) l=md+1; else r=md;
        } i+=l,j+=l;
        l=0,r=l2-j+2;
        if(k==4) {if(j-2>=l2) return 1;}
        else if(j-1>=l2) return 1; 
    } return 0;
}
signed main() {
#ifdef JACK
    freopen("NOIPAK++.in","r",stdin);
#endif
    p[0]=1; for(R i=1;i<=N-10;++i) p[i]=p[i-1]*B;
    t=g(); while(t--) { R ans=0;
        scanf("%s%s",s1+1,s2+1); l1=strlen(s1+1),l2=strlen(s2+1);
        if(l1<l2) {printf("0
"); continue;}
        for(R i=1;i<=l1;++i) h1[i]=h1[i-1]*B+s1[i];
        for(R i=1;i<=l2;++i) h2[i]=h2[i-1]*B+s2[i];
        for(R i=1;i<=l1-l2+1;++i) ans+=ck(i); printf("%d
",ans);
    }
} 

---

2019.06.1011