2019.09.24
T1 100pts
爆搜。没话。
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=20;
int n,a[N],b[N],c[N],d[N],ans1,ans2;
ll ans; bool flg[N];
inline void dfs(int s) {
if(s==n) { ans1=0,ans2=0;
for(R i=1;i<=n;++i) {
if(flg[i]) ans1+=a[i],ans2=max(0,ans2-b[i]);
else ans1=max(0,ans1-d[i]),ans2+=c[i];
} ans=max(ans,1ll*ans1*ans2); return ;
}
for(R i=0;i<=1;++i) {
flg[s+1]=i; dfs(s+1); flg[s+1]=0;
}
}
inline void main() {
n=g(); for(R i=1;i<=n;++i) a[i]=g(),b[i]=g(),c[i]=g(),d[i]=g();
dfs(0); printf("%lld
",ans);
}
} signed main() {Luitaryi::main(); return 0;}
T2 我菜爆了 100pts
别人两个二维前缀和,直接点数-边数???而我四个???
反正过了。
就是把联通快中定一个根节点,所有边都连有向边,最后有几条有向边穿出边界,在算上矩形范围内有几个根节点,就是联通块个数。
注意不要用scanf("%1d",&a[i][j]) 去读入,会增大一倍常数。
#include<bits/stdc++.h>
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=2010,FF=1;
int n,m,q; char c[N]; bool flg[N][N],vis[N][N];
int s1[N][N],s2[N][N],s3[N][N],s4[N][N],s[N][N];
inline void dfs(int i,int j) { vis[i][j]=true; R I=i,J=j+FF;
if(I<1||I>n||J<1||J>m||!flg[I][J]||vis[I][J]) goto nxt1;
s1[I][J]=1,dfs(I,J); nxt1:I=i,J=j-FF;
if(I<1||I>n||J<1||J>m||!flg[I][J]||vis[I][J]) goto nxt2;
s2[I][J]=1,dfs(I,J); nxt2:I=i-FF,J=j;
if(I<1||I>n||J<1||J>m||!flg[I][J]||vis[I][J]) goto nxt3;
s3[I][J]=1,dfs(I,J); nxt3:I=i+FF,J=j;
if(I<1||I>n||J<1||J>m||!flg[I][J]||vis[I][J]) return ;
s4[I][J]=1,dfs(I,J);
}
inline void main() {
n=g(),m=g(),q=g(); for(R i=1;i<=n;++i) {
scanf("%s",c+1); for(R j=1;j<=m;++j)
if(c[j]=='1') flg[i][j]=true;
} for(R i=1;i<=n;++i) for(R j=1;j<=m;++j)
if(flg[i][j]&&!vis[i][j]) s[i][j]=1,dfs(i,j);
for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s1[i][j]+=s1[i-1][j];
for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s2[i][j]+=s2[i-1][j];
for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s3[i][j]+=s3[i][j-1];
for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s4[i][j]+=s4[i][j-1];
for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s[i][j]+=s[i][j-1];
for(R i=1;i<=n;++i) for(R j=1;j<=m;++j) s[i][j]+=s[i-1][j];
while(q--) {
R x1=g(),y1=g(),x2=g(),y2=g();
R ans=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]+s1[x2][y1]-s1[x1-1][y1]+s2[x2][y2]-s2[x1-1][y2]+s3[x2][y2]-s3[x2][y1-1]+s4[x1][y2]-s4[x1][y1-1];
printf("%d
",ans);
}
}
} signed main() {Luitaryi::main(); return 0;}
T3 我要我的分 0pts
考场上写了一个压位+分块(也不知道叫什么),然后MLE了
实际上我只开了23MB,并且换了不同的评测机获得了70pts-80pts
不管什么,先展示一波
#include<iostream>
#include<cstdio>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=3125000,B=32;
int L; ll ans;
unsigned int mem[N+20],c[N+20];
inline int query(int p) { R ret=0;
for(;p;p-=p&-p) ret+=c[p]; return ret;
}
inline void add(int p) {for(;p<=L;p+=p&-p) ++c[p];}
inline void main() {
R n=g(),X=g(),A=g(),p=g();
const int P=p; L=(P+B-1)/B;
for(R i=1,p1,p2,tmp;i<=n;++i) {
p1=X/B+1,p2=X%B;
ans+=i-query(p1)-1;
tmp=mem[p1]>>p2;
while(tmp) tmp-=tmp&-tmp,++ans;
add(p1),mem[p1]|=1u<<p2;
X=(X+A)%P;
} printf("%lld
",ans);
}
} signed main() {Luitaryi::main(); return 0;}
(mathcal{O}(32*n))
好的我们来说正解。观察到 (a) 很小,所以我们考虑如何把时间 or 空间 复杂度放到 (a) 上
我们发现,取模前,这些数字构成了等差数列,大致长这样:
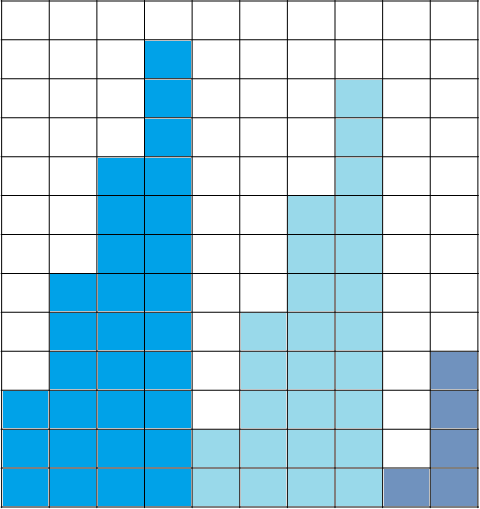
然后我们发现,对于后面的段,很容易考虑他能与前面的段产生的贡献:我们看有多少个端首大于当前段首。
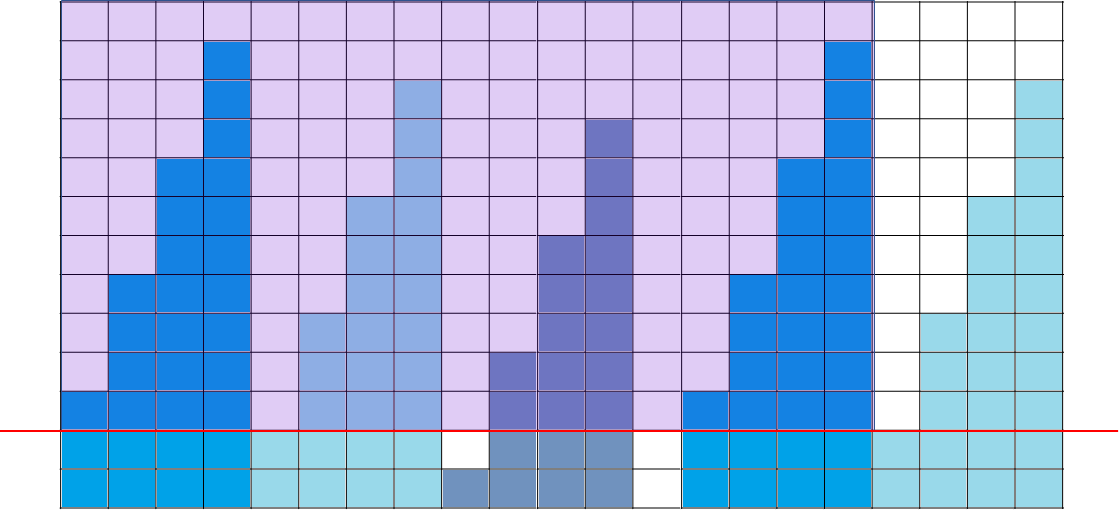
这样我们向上推一格只用把贡献减掉之前的段数就ok了。

注意如果刚开始 (X) 比较大,要少减1。详见代码
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=100000;
int c[N+10]; ll ans;
inline void add(int p) {++p; for(;p<=N;p+=p&-p) ++c[p];}
inline int query(int p) { R ret=0; ++p;
for(;p;p-=p&-p) ret+=c[p]; return ret;
}
inline void main() {
R n=g(),X=g(),A=g(),P=g(),k=0,sum=0,cur; cur=X;
for(R i=1;i<=n;++i) {
if(cur>=A) {
sum-=k;
if(X>cur) ++sum;//上面-k多减了1,因为第一个等差数列并没有小于X的数
ans+=sum;
} else
sum=i-query(cur)-1,//比他大的等差数列的第一项
ans+=sum,
add(cur);
cur+=A; if(cur>=P) cur-=P,++k;
} printf("%lld
",ans);
}
} signed main() {Luitaryi::main(); return 0;}
这个卡空间也是服了。
2019.09.26
T1 100pts
考试时明明已经暴力开根了却还倍增+二分我是沙雕
std是啥现在还不会
于是我隆重介绍一下瞎搞算法:( exttt{pow}) 暴力开根。
我不是不知道你是几次方吗,那我就从大往小开,直到开出来或者 (>1000) 直接 break;
然后判一下相等的,然后暴力找等比(毕竟长度是 (log) 的)(其实可以双指针,但是相等导致有些难判,懒得写了)
注意 ( exttt{pow}) 有时候会开的小一些,所以同时检验一下+1
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline ll g() { register ll x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=100010,B=58,MX=1000;
map<ll,bool> mp;
int n,ans=1,a[N]; ll mem[N];
inline ll qpow(ll a,ll p) { register ll ret=1;
for(;p;p>>=1,a*=a) if(p&1) ret*=a; return ret;
}
inline void main() {
n=g(); register ll U,D=1; for(R i=1;i<=n;++i) {
mem[i]=U=g(); if(U<D) swap(U,D);
if(U%D==0) {
register ll tmp=U/D;
for(R j=B;j;--j) {
register ll t=pow(tmp,1.0/j);
if(t>MX) break;
if(qpow(t,j)==tmp) {a[i-1]=t; break;}
if(qpow(t+1,j)==tmp) {a[i-1]=t+1; break;}
}
} D=mem[i];
} for(R i=1,j;i<n;++i) if(a[i]==1) { j=i;
while(a[j+1]==1) ++j; ans=max(ans,j-i+2); i=j;
}
for(R i=1;i<n;++i) if(a[i]) {
mp.clear(); mp[mem[i]]=true;
for(R j=i;!mp[mem[j+1]]&&a[i]==a[j]&&j<n;++j)
ans=max(ans,j-i+2),mp[mem[j+1]]=true;
} printf("%d
",ans);
}
} signed main() {Luitaryi::main(); return 0;}
T2 菜死了 35pts
直接正解:
(f[u][j][0/1]) 表示子树中最大深度为 (j) 链的方案数,(0/1) 表示是否安排重儿子;
(s[u][j][0/1]) 表示子树中最大深度小于等于 (j) 链的方案数;
(h[j][0/1]) 临时数组。
#include<bits/stdc++.h>
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=3010,M=1000000007;
int n,cnt,Inv=1,rt,ans; bool flg[N];
int vr[N<<1],nxt[N<<1],fir[N];
int f[N][N][2],h[N][2],s[N][N][2];
inline void add(int u,int v) {
vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;
vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt;
}
inline int qpow(int a,int b) { R ret=1;
for(;b;b>>=1,a=1ll*a*a%M) if(b&1) ret=1ll*ret*a%M; return ret;
}
inline void dfs(int u,int fa) {
f[u][0][0]=1; R num=0;
for(R i=0;i<=n;++i) s[u][i][0]=1;
for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
if(v==fa) continue; ++num;
dfs(v,u); memset(h,0,sizeof h);
h[0][1]=1ll*f[u][0][0]*f[v][0][1]%M; //深度为0特殊处理。
for(R j=1;j<=n;++j) {
h[j][0]=(h[j][0]+1ll*f[u][j][0]*s[v][j-1][1]+1ll*f[v][j-1][1]*s[u][j-1][0])%M;
//如果之前的孩子已经有深度为j的链了,现在的孩子v就可以选j-1及以下的链;如果还没有,那么强制v选长度为j的链,之前的孩子选j-1及以下的都可以。
h[j][1]=(h[j][1]+1ll*f[u][j][1]*s[v][j-1][1]+1ll*s[u][j-1][1]*f[v][j-1][1])%M; //之前安排了重儿子
h[j][1]=(h[j][1]+1ll*f[u][j][0]*s[v][j-1][1]+1ll*s[u][j-1][0]*f[v][j][1]+1ll*f[u][j][0]*f[v][j][1])%M; //让现在的当重儿子
}
memcpy(s[u],h,sizeof h),memcpy(f[u],h,sizeof h);
for(R j=1;j<=n;++j)
s[u][j][0]=(s[u][j][0]+s[u][j-1][0])%M,
s[u][j][1]=(s[u][j][1]+s[u][j-1][1])%M;
}
if(!num) {f[u][0][1]=1; for(R i=0;i<=n;++i) s[u][i][1]=1;}
else Inv=1ll*Inv*num%M;
}
inline void main() {
n=g(); for(R i=1,x,v;i<=n;++i) {
x=g(); while(x--) v=g(),add(i,v),flg[v]=true;
} for(R i=1;i<=n;++i) if(!flg[i]) dfs(rt=i,0);
for(R i=0;i<=n;++i) ans=(ans+1ll*i*f[rt][i][1])%M;
printf("%d
",1ll*ans*qpow(Inv,M-2)%M);
}
} signed main() {Luitaryi::main(); return 0;}
T3 又被了 0pts
考试时没有写。
观察题意,发现,加边和减边,相当于我们在 (C(n,2)) 条边中选一条边把他改成相反状态。所以我们只用求出欧拉回路的方案数 (*C(n,2)) 就可以了。
那么偶度数的无向图(不保证联通)的方案数是 (2^{C_{i-1}^2}) ,可以理解为从 (i-1) 个点构成的图中任意连边,然后把奇度数的点连到 (i) 上,因为一条边贡献两个度数,所以奇度数的点一定只有偶数个。
剩下的就是套路了,知道不连通的如何求联通的:枚举关键点和联通块的大小。
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=2010,M=1000000007;
inline int qpow(int a,int b) { R ret=1;
for(;b;b>>=1,a=1ll*a*a%M) if(b&1) ret=1ll*ret*a%M; return ret;
}
int n,h[N],f[N],fac[N],rfac[N],Inv[N];
inline int C(int n,int m) {return 1ll*fac[n]*rfac[n-m]%M*rfac[m]%M;}
inline void main() { n=g();
fac[0]=fac[1]=1; for(R i=2;i<=n;++i) fac[i]=1ll*fac[i-1]*i%M;
Inv[0]=Inv[1]=1; for(R i=2;i<=n;++i) Inv[i]=M-1ll*M/i*Inv[M%i]%M;
rfac[0]=rfac[1]=1; for(R i=2;i<=n;++i) rfac[i]=1ll*rfac[i-1]*Inv[i]%M;
f[1]=h[1]=1;
for(R i=2;i<=n;++i) { f[i]=h[i]=qpow(2,(i-1)*(i-2)/2);;
for(R j=1;j<i;++j) f[i]=(f[i]-1ll*C(i-1,j-1)*f[j]%M*h[i-j]%M+M)%M;
} printf("%d
",1ll*f[n]*(n-1)*n/2%M);
}
} signed main() {Luitaryi::main(); return 0;}
2019.09.28
T1 爆零 0pts
考试时不知道自己在想啥,写了个错误的暴力,然后就开始优化暴力。
如果想看我当初如何想的,可以去做这个
正解:我们发现,如果 (n-1) 在 (n) 的后面,那一定要把他挪到最前面,其他数依次挪到 (n-1) 的前面就够了。这样代价是 (n-1)。
若如果 (n-1) 在 (n) 的 前面,那就检查 (n-2) 是否在 (n-1) 的后面,直到出现逆序。
#include<bits/stdc++.h>
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=100010;
int T,n,pos[N];
inline void main() {
freopen("book.in","r",stdin);
freopen("book.out","w",stdout);
T=g(); while(T--) {
n=g(); for(R i=1;i<=n;++i)
pos[g()]=i; pos[n+1]=n+1;
for(;n;--n) if(pos[n+1]<pos[n])
{printf("%d
",n); break;}
}
}
} signed main() {Luitaryi::main(); return 0;}
T2 我傻 65pts
最后没有对所有体积取 (max) 还好给了我点分
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=1010,M=3010;
int T,n,t;
ll f[M],ans;
struct node { int a,b,c;
inline bool operator < (const node& that) const {return 1ll*that.b*c<1ll*b*that.c;}
}s[N];
inline void main() {
freopen("score.in","r",stdin);
freopen("score.out","w",stdout);
T=g(); while(T--) { ans=0;
n=g(),t=g(); //for(R i=1;i<=n;++i) a[i]=g(),b[i]=g(),c[i]=g();
for(R i=1;i<=n;++i) s[i].a=g(),s[i].b=g(),s[i].c=g();
sort(s+1,s+n+1);
for(R i=1;i<=n;++i) for(R j=t;j>=s[i].c;--j) {
f[j]=max(f[j-s[i].c]+s[i].a-1ll*s[i].b*j,f[j]);
}
for(R i=0;i<=t;++i) ans=max(ans,f[i]);
printf("%lld
",ans);
memset(f,0,sizeof f);
}
fclose(stdin),fclose(stdout);
}
} signed main() {Luitaryi::main(); return 0;}
T3 又双叒叕傻了 60pts
数组正好开成 (250)。。怕不是正好形容我。。。
开大了能得 (80pts)。 对树桩sort后能100pts竟然只有400ms左右(玄学spfa+O2)不开O2 1300ms左右
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=260; const ll Inf=0x3f3f3f3f3f3f3f3f;
struct node { int x,y; node() {}
node(int _x,int _y) {x=_x,y=_y;}
inline bool operator < (const node& that) const
{return y<that.y||(y==that.y&&x<that.x);}
}a[N];
struct cir { int r,c;
inline bool operator < (const cir& that) const
{return r>that.r||(r==that.r&&c<that.c);}
}b[N];
int T,n,m,w;
ll dis[N][N],f[N][N],ans=Inf; bool vis[N][N];
queue<node> q;
inline void spafa() {
while(q.size()) {
register node t=q.front(); q.pop(); R i=t.x,k=t.y; vis[i][k]=false;
for(R j=1;j<=n;++j) if(i!=j) {
for(R p=1;p<=m;++p) {
if(dis[i][j]>1ll*(b[k].r+b[p].r)*(b[k].r+b[p].r)) break;
if(f[j][p]>f[i][k]+b[p].c) {
f[j][p]=f[i][k]+b[p].c;
if(!vis[j][p]) q.push(node(j,p)),vis[j][p]=true;
}
}
}
}
}
inline void main() {
T=g(); while(T--) { ans=Inf;
n=g(),m=g(),w=g();
for(R i=1;i<=n;++i) a[i].x=g(),a[i].y=g();
for(R i=1;i<=m;++i) b[i].r=g(),b[i].c=g();
sort(a+1,a+n+1); sort(b+1,b+m+1); R mn=1e9,tot=0;
for(R i=1;i<=n;++i) for(R j=1;j<=n;++j)
dis[i][j]=1ll*(a[i].x-a[j].x)*(a[i].x-a[j].x)+1ll*(a[i].y-a[j].y)*(a[i].y-a[j].y);
for(R i=1;i<=m;++i) if(b[i].c<mn) b[++tot]=b[i],mn=b[i].c;
memset(f,0x3f,sizeof f); m=tot;
for(R i=1;i<=n;++i) for(R j=1;j<=m&&b[j].r>=a[i].y;++j) {
f[i][j]=b[j].c; if(!vis[i][j])
q.push(node(i,j)),vis[i][j]=true;
}
//for(R i=1;i<=n;++i,cout<<endl) for(R j=m;j;--j) cout<<f[i][j]<<' ';
spafa(); for(R i=1;i<=n;++i) for(R j=1;j<=m&&b[j].r>=w-a[i].y;++j)
ans=min(ans,f[i][j]);
//for(R i=1;i<=n;++i,cout<<endl) for(R j=m;j;--j) cout<<f[i][j]<<' ';
if(ans>=Inf/2) puts("impossible");
else printf("%lld
",ans);
}
fclose(stdin),fclose(stdout);
}
} signed main() {Luitaryi::main(); return 0;}
以上是暴力。
正解:我们这样连边:
设已经去掉无用的圆盘(即去掉又小又贵的)并已从小到大排好。
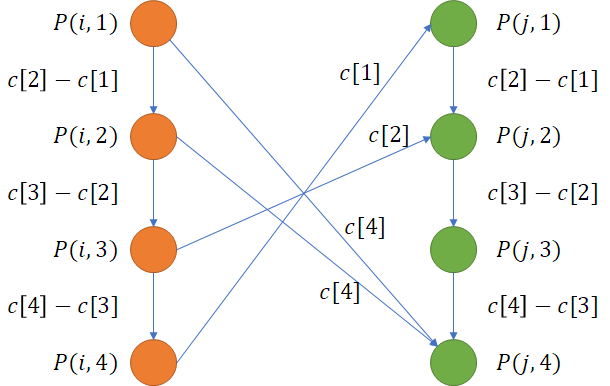
用 dijk 会非常快吗,spfa大约会T。
#pragma GCC optimize(2)
#include<bits/stdc++.h>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*f;
} const int N=260,M=N*N*N; const ll Inf=0x3f3f3f3f3f3f3f3f;
struct node { int x,y; node() {}
node(int _x,int _y) {x=_x,y=_y;}
inline bool operator < (const node& that) const
{return y<that.y||(y==that.y&&x<that.x);}
}a[N];
struct cir { int r,c;
inline bool operator < (const cir& that) const
{return r>that.r||(r==that.r&&c<that.c);}
}b[N];
int T,n,m,W,cnt; bool vis[N*N];
ll dis[N][N],d[N*N],ans;
int vr[M],nxt[M],fir[N*N],w[M];
inline void add(int u,int v,int ww) {vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;}
priority_queue<pair<ll,int> > q;
inline void dijk() {
while(q.size()) { R u=q.top().second; q.pop();
for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
if(d[v]>d[u]+w[i]) d[v]=d[u]+w[i],q.push(make_pair(-d[v],v));
}
}
}
#define P(i,j) ((i-1)*m+j)
inline void main() {
T=g(); while(T--) { ans=Inf; cnt=0;
n=g(),m=g(),W=g();
for(R i=1;i<=n;++i) a[i].x=g(),a[i].y=g();
for(R i=1;i<=m;++i) b[i].r=g(),b[i].c=g();
sort(a+1,a+n+1);
sort(b+1,b+m+1); R mn=1e9,tot=0;
for(R i=1;i<=n;++i) for(R j=1;j<=n;++j)
dis[i][j]=1ll*(a[i].x-a[j].x)*(a[i].x-a[j].x)+1ll*(a[i].y-a[j].y)*(a[i].y-a[j].y);
for(R i=1;i<=m;++i) if(b[i].c<mn) b[++tot]=b[i],mn=b[i].c;
memset(d,0x3f,sizeof d); m=tot,reverse(b+1,b+m+1);
for(R i=1;i<=n;++i) for(R j=1;j<=n;++j) if(i!=j) { R p=m,pre=0;
for(R k=1;k<=m;++k) {
if(dis[i][j]<=1ll*(b[k].r+b[m].r)*(b[k].r+b[m].r)) {
if(!pre) pre=k; else add(P(i,pre),P(i,k),b[k].c-b[pre].c),pre=k;
while(p>0&&dis[i][j]<=1ll*(b[k].r+b[p].r)*(b[k].r+b[p].r)) --p;
add(P(i,k),P(j,p+1),b[p+1].c);
}
}
}
for(R i=1;i<=n;++i) for(R j=m;j&&b[j].r>=a[i].y;--j)
{d[P(i,j)]=b[j].c; q.push(make_pair(-d[P(i,j)],P(i,j))),vis[P(i,j)]=true;}
dijk(); for(R i=1;i<=n;++i) for(R j=m;j&&b[j].r>=W-a[i].y;--j)
ans=min(ans,d[P(i,j)]);
if(ans>=Inf/2) puts("impossible");
else printf("%lld
",ans);
memset(fir,0,sizeof(fir));
memset(nxt,0,sizeof(int)*(cnt+1));
}
}
} signed main() {Luitaryi::main(); return 0;}