Luogu P1646 [国家集训队]happiness

在二元关系中，去除一个割，剩下的部分还是一个割。

所以这道题我们可以转化为 总权值 - 最小割 来解决最大化的问题。

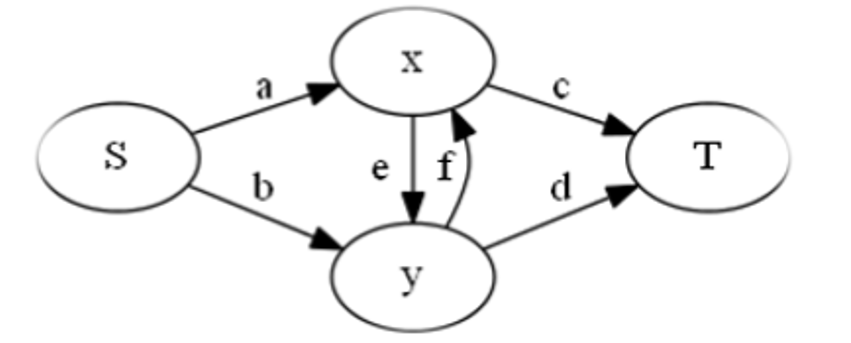
具体地，我们设 (A_x) 表示 (x) 选文科的贡献，设 (B_x) 表示 (x) 选理科的贡献，(A_{x,y}) 表示同时选文科的贡献，(B_{x,y}) 表示同时选理科的贡献；并且设割哪条边代表不选哪一科：

总权值：(a+b+c+d+e+f=A_x+B_x+A_y+B_y+A_{x,y}+B_{x,y})

同时选理：(a+b=A_x+A_y+A_{x,y} (1))

同时选文：(c+d= B_x+B_y+B_{x,y} (2))

(x) 选文，(y) 选理：(b+c+e= B_x+A_y+A_{x,y}+B_{x,y} (3))

(x) 选理，(y) 选文：(a+d+f= A_x+B_y+A_{x,y}+B_{x,y} (4))

((3)+(4)-(1)-(2)) 得：

(e+f=A_{x,y}+B_{x,y})，我们令 (e=f=frac{A_{x,y}+B_{x,y}}{2}) 。

我们令 (a=A_x+frac{A_{x,y}}{2})，则有：

(b=A_y+frac{A_{x,y}}{2},c=B_x+frac{B_{x,y}}{2},d=B_y+frac{B_{x,y}}{2})

在实际运算过程中，我们可以把边权 ( imes 2) 避免浮点数。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define R register int
using namespace std;
namespace Luitaryi {
inline int g() { R x=0,f=1;
  register char s; while(!isdigit(s=getchar())) f=s=='-'?-1:f;
  do x=x*10+(s^48); while(isdigit(s=getchar())); return x*f;
} const int L=105,N=10010,M=200010,Inf=0x3f3f3f3f;
int n,m,cnt=1,ans,s,t,a[L][L],b[L][L];
int vr[M],nxt[M],w[M],fir[N],cur[N],d[N];
inline void add(int u,int v,int ww) {
  vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;
  vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt,w[cnt]=0;
}
inline void adde(int u,int v,int ww) {
  vr[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt,w[cnt]=ww;
  vr[++cnt]=u,nxt[cnt]=fir[v],fir[v]=cnt,w[cnt]=ww;
}
queue<int> q;
inline bool bfs() {
	memset(d,0,sizeof d),memcpy(cur,fir,sizeof cur);
	d[s]=1,q.push(s); while(q.size()) {
		R u=q.front(); q.pop();
		for(R i=fir[u];i;i=nxt[i]) if(w[i]) {
			R v=vr[i]; if(!d[v]) d[v]=d[u]+1,q.push(v);
		}
	} return d[t];
}
inline int dfs(int u,int f) {
	if(u==t||f<=0) return f; R res=f;
	for(R& i=cur[u];i;i=nxt[i]) if(w[i]) {
		R v=vr[i]; if(d[v]==d[u]+1) {
			R tmp=dfs(v,min(res,w[i]));
			if(!tmp) d[v]=0;
			res-=tmp,w[i]-=tmp,w[i^1]+=tmp;
			if(!res) return f;
		}
	} return f-res;
}
inline int dinic() {R ret=0; while(bfs()) ret+=dfs(s,Inf); return ret;}
#define p(i,j) ((i-1)*m+j)
inline void main() {
  n=g(),m=g(),s=0,t=n*m+1;
  for(R i=1;i<=n;++i) for(R j=1;j<=m;++j)
    ans+=(a[i][j]=g()),a[i][j]<<=1;
  for(R i=1;i<=n;++i) for(R j=1;j<=m;++j)
    ans+=(b[i][j]=g()),b[i][j]<<=1;
  for(R i=1,x;i<n;++i) for(R j=1;j<=m;++j)
    x=g(),ans+=x,a[i][j]+=x,a[i+1][j]+=x,
    adde(p(i,j),p(i+1,j),x);
  for(R i=1,x;i<n;++i) for(R j=1;j<=m;++j)
    x=g(),ans+=x,b[i][j]+=x,b[i+1][j]+=x,
    adde(p(i,j),p(i+1,j),x);
  for(R i=1,x;i<=n;++i) for(R j=1;j<m;++j)
    x=g(),ans+=x,a[i][j]+=x,a[i][j+1]+=x,
    adde(p(i,j),p(i,j+1),x);
  for(R i=1,x;i<=n;++i) for(R j=1;j<m;++j)
    x=g(),ans+=x,b[i][j]+=x,b[i][j+1]+=x,
    adde(p(i,j),p(i,j+1),x);
  for(R i=1;i<=n;++i) for(R j=1;j<=m;++j)
    add(s,p(i,j),a[i][j]),add(p(i,j),t,b[i][j]);
  printf("%d
",ans-dinic()/2);
}
} signed main() {Luitaryi::main(); return 0;}

---

2019.12.30