题目描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
这道题目是考察如何改变指针达到要求,什么是二叉搜索树在这里再放一下:
二叉搜索树是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树,如下图所示就是一个二叉搜索树:
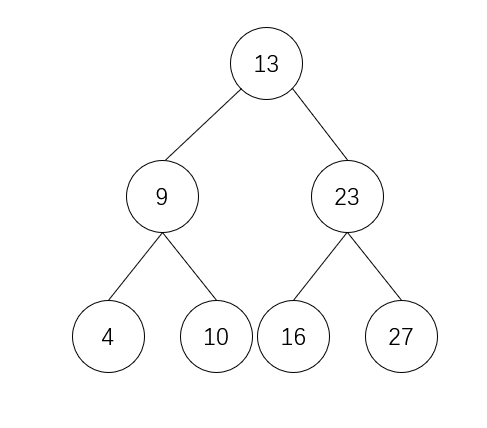
根据这个图,我们其实可以看出,叶节点部分的最小二叉树按照左子树节点——根节点——右子树节点来排序的话恰好是一个从小到大排序的数组:

这道题目的思路其实是我们先找到最大的节点,也就是一直向右子树找,直到右子树为空,那么这个节点就是值最大的节点,我们将其记录为pre,接下来我们要改变这个值最大的节点与他的父节点的指针指向,在这里我们用23和27举例,首先将23的右子树指向27,然后将27的左子树指向23,这里要改变一下pre,将pre重新复制为27节点记录下来,以进行后续操作。这样就暂且完成了两个节点的连接,如下:
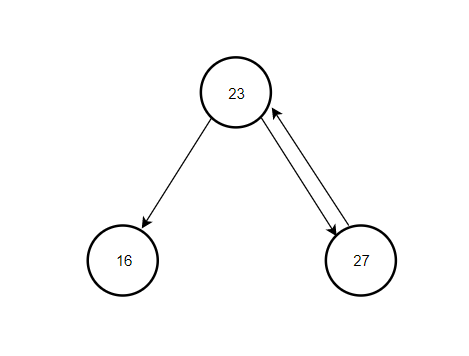
接下来我们考虑一下23的左子树16的指针变化,很简单,将16的右子树指针指向23,然后再改变pre,将其赋值为16节点,如下:
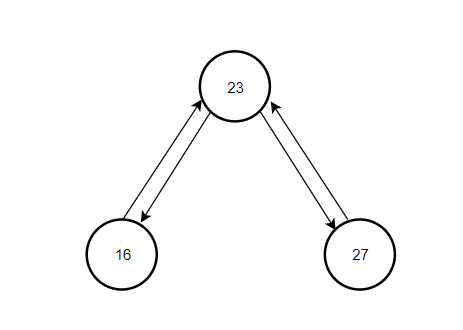
看到这里大家明白没有,pre记录的其实是从最大值节点开始,逐渐改为倒数第二大值节点和倒数第三大值节点,以此类推。所以我们没有只要改变pre记录的节点指针的指向就可以,pre以右的所有指针都是已经排好序的
我这里考虑的是比较简单的情况,其实复杂的情况也是这个规律,找好规律让递归算法完成就可以了。
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
function Convert(pRootOfTree)
{
let pre = null;
function _Convert(_pRootOfTree){
if(!_pRootOfTree){return null;}
_Convert(_pRootOfTree.right);
if(!pre){pre=_pRootOfTree;}
else{
_pRootOfTree.right = pre;
pre.left = _pRootOfTree;
pre = _pRootOfTree;
}
_Convert(_pRootOfTree.left);
return pre;
}
return _Convert(pRootOfTree);
}